Capítulos
Un número compuesto es el que posee más de dos divisores. Es decir, aquel que se puede dividir por sí mismo, por la unidad y por otros números.
Ejemplos:
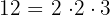
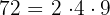
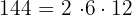
Los números compuestos se pueden expresar como productos de potencias de números primos. A dicha expresión se le llama descomposición de un número en factores primos.
Ejemplos:
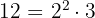
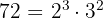
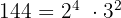

Factorizar un número
Para factorizar un número o descomponerlo en factores efectuamos sucesivas divisiones entre sus divisores primos hasta obtener un 1 como cociente.
Para factorizar utilizaremos una barra vertical, a la derecha escribimos los divisores primos y a la izquierda las sucesivas divisiones.
Ejemplo:
1 Factorizar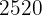
Como el número termina en cifra par es divisible por  , colocamos el
, colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos 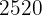 por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda
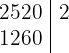
 termina en
termina en  , por tanto también es divisible por
, por tanto también es divisible por  , colocamos el
, colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos  por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda
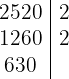
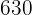 termina en
termina en  , por tanto también es divisible por
, por tanto también es divisible por  , colocamos el
, colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos 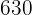 por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda

Como no to termina en cifra par ni en  no es divisible por
no es divisible por  , entonces probamos por
, entonces probamos por  . La suma de las cifras de
. La suma de las cifras de  es igual a
es igual a  que divisible por
que divisible por  . Colocamos el
. Colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos  por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda
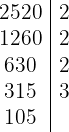
Volvemos a probar por  . La suma de las cifras de
. La suma de las cifras de  es igual a
es igual a  que divisible por
que divisible por  . Colocamos el
. Colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos  por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda

Volvemos a probar por  . La suma de las cifras de
. La suma de las cifras de  es igual a
es igual a  que no es divisible por
que no es divisible por  , por tanto tenemos que probar por el siguiente número primo que es
, por tanto tenemos que probar por el siguiente número primo que es  , como
, como  termina en
termina en  es divisible entre
es divisible entre  . Colocamos el
. Colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos  por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda

 es un número primo, por tanto es divisible por sí mismo. Colocamos el
es un número primo, por tanto es divisible por sí mismo. Colocamos el  a la derecha de la raya
a la derecha de la raya
Dividimos  por
por  y lo colocamos a la izquierda
y lo colocamos a la izquierda

Una vez que llegamos a  termina la factorización
termina la factorización
Como a la derecha tenemos el  repetido tres veces, el
repetido tres veces, el  repetido dos veces, el
repetido dos veces, el  y el
y el  ; la factorización será:
; la factorización será:
Solución: 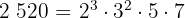
2 Factorizar 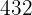
Ejemplo:

Solución:
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)