Calcula el valor del determinante

1La primera columna es un múltiplo de 2, entonces
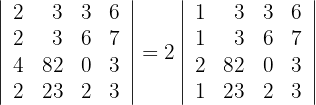
2Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas  por
por  respectivamente y obtenemos
respectivamente y obtenemos
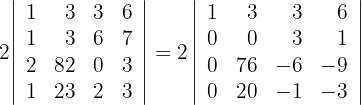
3Para la primera columna que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
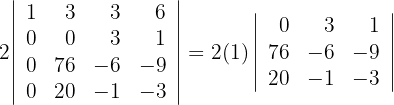
4Aplicamos la regla de Sarrus y obtenemos
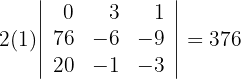
Aplicando las propiedades de los determinantes, calcular:
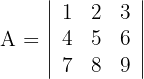
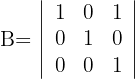
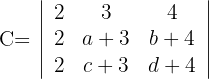
Determinante A
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas  por
por  respectivamente y obtenemos
respectivamente y obtenemos
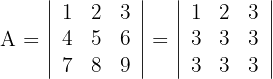
2Como se tienen dos filas iguales, las propiedades de los determinantes nos dicen que el resultado es cero
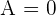
Determinante B
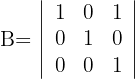
1Como se trata de una matriz triangular, las propiedades de los determinantes nos dicen que el resultado es el producto de los elementos de la diagonal
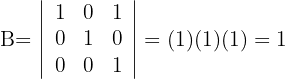
Determinante C
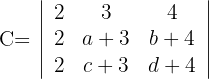
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas  por
por 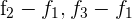 respectivamente y obtenemos
respectivamente y obtenemos
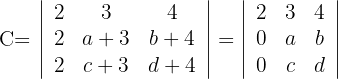
2Para la primera columna que contiene 2 ceros, aplicamos la matriz reducida y obtenemos
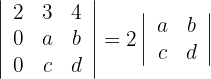
3Calculamos el último determinante y obtenemos
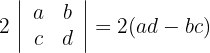
Aplicando las propiedades de los determinantes, calcular:


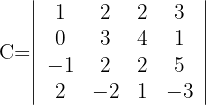
Determinante A
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas 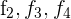 por
por 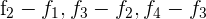 respectivamente y obtenemos
respectivamente y obtenemos

2Nuevamente reemplazamos las filas 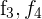 por
por 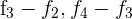 respectivamente y obtenemos
respectivamente y obtenemos
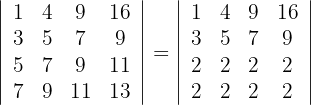
3Como se tienen dos filas iguales, las propiedades de los determinantes nos dicen que el resultado es cero, esto es, 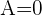
Determinante B
1Como el valor del determinante no cambia bajo combinación lineal de las columnas, reemplazamos las columnas 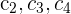 por
por  respectivamente y obtenemos
respectivamente y obtenemos
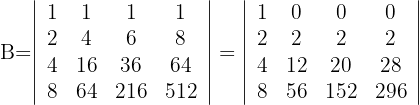
2Para la primera fila que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
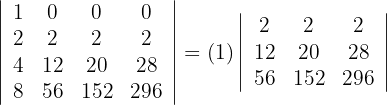
3La primera fila es un múltiplo de 2, entonces
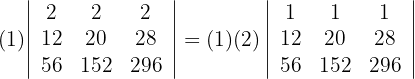
4Como el valor del determinante no cambia bajo combinación lineal de las columnas, reemplazamos las columnas 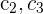 por
por 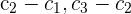 respectivamente y obtenemos
respectivamente y obtenemos
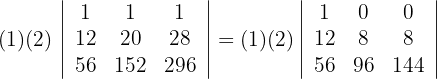
5Para la primera fila que contiene 2 ceros, aplicamos la matriz reducida y obtenemos
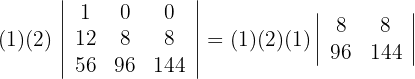
6Calculamos el determinante para la matriz de 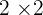
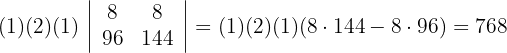
Determinante C
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas 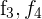 por
por 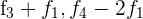 respectivamente y obtenemos
respectivamente y obtenemos
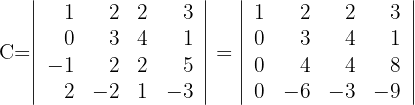
2Para la primera columna que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
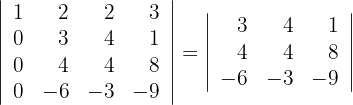
3La segunda fila es un múltiplo de 4 y la tercera es un múltiplo de -3, entonces
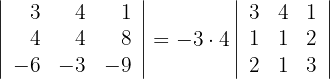
4Resolvemos el último determinante obtenido
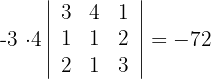
Pasando a determinantes triangulares, calcular el valor de:
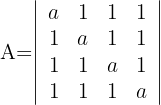

Determinante A
1Como el valor del determinante no cambia bajo combinación lineal de las columnas, reemplazamos 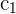 por
por  y obtenemos
y obtenemos
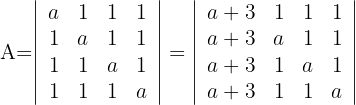
2Como la primera columna es un múltiplo de  , se tiene
, se tiene
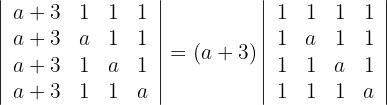
3Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas  por
por  respectivamente y obtenemos
respectivamente y obtenemos
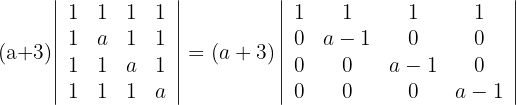
4El determinante de una matriz triangular es igual al producto de los elementos de la diagonal
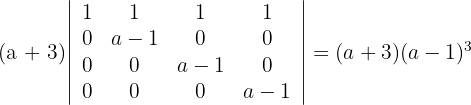
Determinante B
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas  por
por 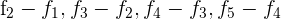 respectivamente y obtenemos
respectivamente y obtenemos
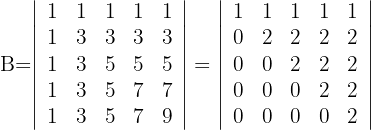
2El determinante de una matriz triangular es igual al producto de los elementos de la diagonal
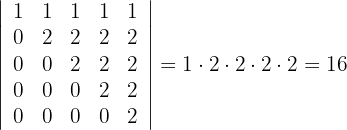
Calcular los determinantes de Vandermonde:
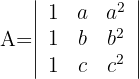
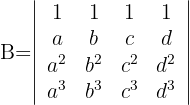
Determinante A
1Como el valor del determinante no cambia bajo combinación lineal de las columnas, reemplazamos 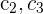 por
por 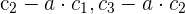 respectivamente y obtenemos
respectivamente y obtenemos
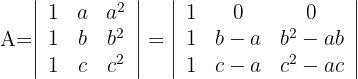
2Para la primera fila que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
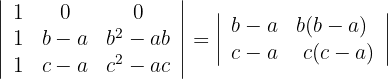
3Los elementos de la primera fila tienen un factor en común; lo mismo sucede para la segunda fila. Estos factores los sacamos del determinante y resolvemos el determinante obtenido
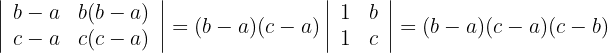
Determinante B
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos 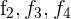 por
por 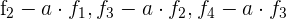 respectivamente y obtenemos
respectivamente y obtenemos
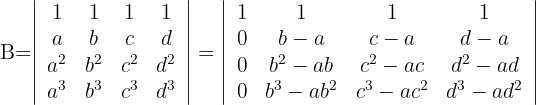
2Para la primera columna que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
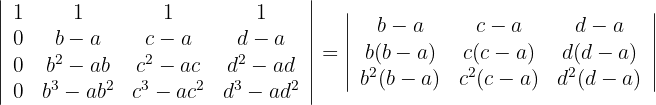
3Los elementos de la primera columna tienen un factor en común; lo mismo sucede el resto de las columnas. Estos factores los sacamos del determinante
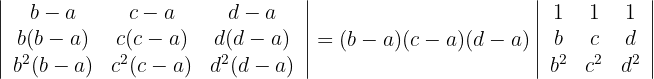
4Reemplazamos 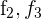 por
por 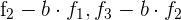 respectivamente y obtenemos
respectivamente y obtenemos
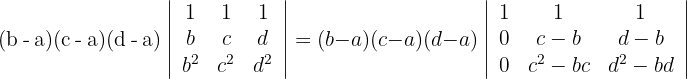
5Para la primera columna que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
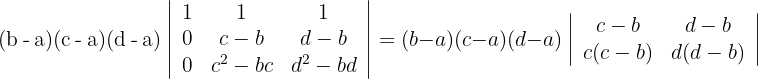
6Los elementos de la primera columna tienen un factor en común; lo mismo sucede para la segunda columna. Estos factores los sacamos del determinante y resolvemos el determinante obtenido
Calcular el valor de los siguientes determinantes:


Determinante A
1Como el valor del determinante no cambia bajo combinación lineal de las columnas, reemplazamos 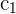 por
por 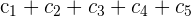 y obtenemos
y obtenemos
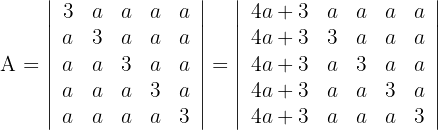
2Como la primera columna es un múltiplo de  , se tiene
, se tiene
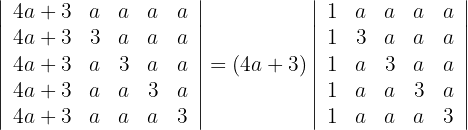
3Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos las filas  por
por 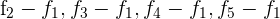 respectivamente y obtenemos
respectivamente y obtenemos
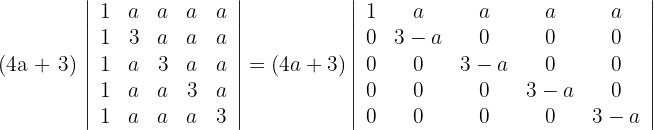
4El determinante de una matriz triangular es igual al producto de los elementos de la diagonal
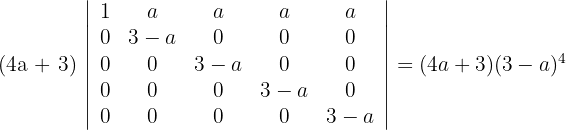
Determinante B
1Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos 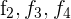 por
por 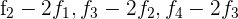 y obtenemos
y obtenemos
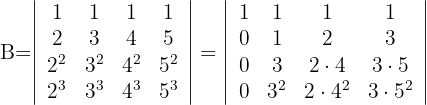
2Para la primera columna que contiene 3 ceros, aplicamos la matriz reducida y obtenemos
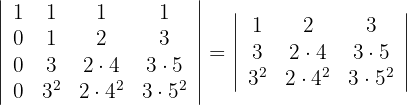
3Como la segunda columna es un múltiplo de  y la tercera columna es un múltiplo de
y la tercera columna es un múltiplo de  , se tiene
, se tiene
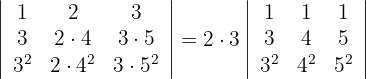
4Como el valor del determinante no cambia bajo combinación lineal de las filas, reemplazamos  por
por  y obtenemos
y obtenemos
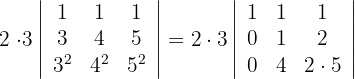
5Para la primera columna que contiene 2 ceros, aplicamos la matriz reducida y obtenemos
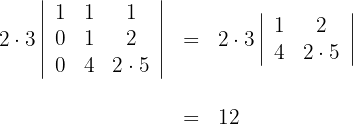
Demostrar, sin desarrollar, que los siguientes determinantes valen cero:
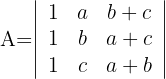
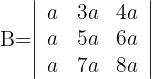
Determinante A
1Como el valor del determinante no cambia bajo combinación lineal de las columnas, reemplazamos 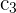 por
por 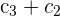 y obtenemos
y obtenemos
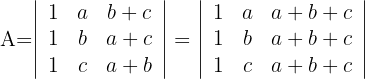
2La tercera columna posee un factor común, luego
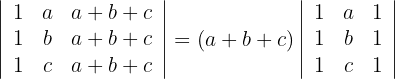
3La primera y tercera columna son iguales por lo que el determinante es cero
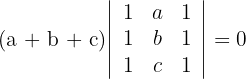
Determinante B
1La tercera columna es igual a la suma de la primera con la segunda, luego el determinante es cero
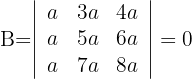
Si el valor del determinante
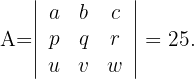
Calcular el valor de
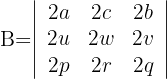
1Como las filas tienen como factor común el valor 2, se tiene
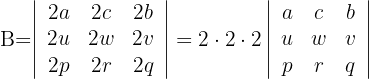
2Intercambiamos las columnas dos y tres
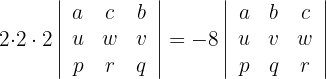
3Intercambiamos las filas dos y tres
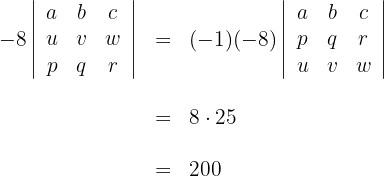
Sabiendo que 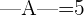 , calcula los otros determinantes:
, calcula los otros determinantes:
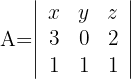
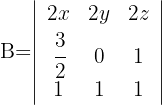
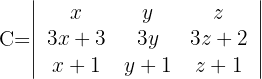
Determinante B
1La fila uno posee un factor común, lo mismo para la segunda fila
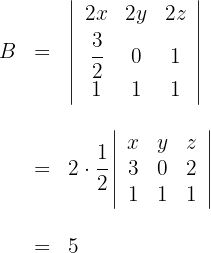
Determinante C
1Reemplazamos las filas 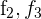 por
por 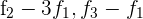 respectivamente
respectivamente
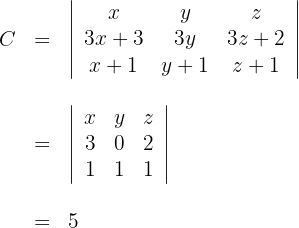
Demostrar que los siguientes determinantes son múltiplos de 5 y 4 respectivamente, sin desarrollarlos
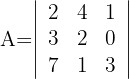
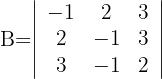
Determinante A
1Reemplazamos la columna 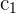 por
por 
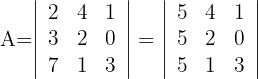
2La columna 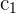 tiene por factor común el 5
tiene por factor común el 5
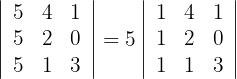
Luego el determinante es un múltiplo de 5
Determinante B
1Reemplazamos la columna 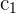 por
por 
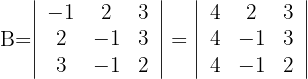
2La columna 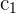 tiene por factor común el 4
tiene por factor común el 4
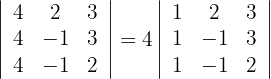
Luego el determinante es un múltiplo de 4
Demostrar, sin desarrollar, que el siguiente determinante es múltiplo de 15:
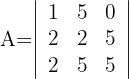
1Reemplazamos la columna 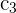 por
por 
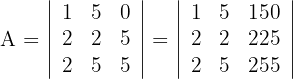
2La columna 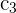 tiene por factor común el 15
tiene por factor común el 15
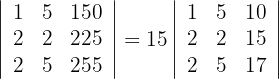
Luego el determinante es un múltiplo de 15
Demostrar que el siguiente determinante es divisible por 21:

1Reemplazamos la columna 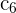 por
por 

2La columna  tiene por factor común el 21
tiene por factor común el 21

Luego el determinante es un múltiplo de 21, así el determinante es divisible por 21
Demuéstrese las igualdades que se indican, sin necesidad de desarrollar los determinantes:
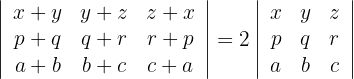
Primera igualdad
1Para el primer determinante utilizamos la propiedad de que las columnas están formados por dos sumandos, entonces el determinante se descompone en la suma de dos determinantes en los que las demás columnas permanecen invariantes. Realizamos para la primera columna
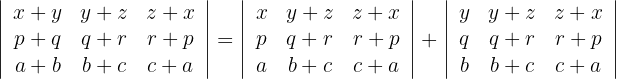
2Volvemos a aplicar la propiedad anterior para cada uno de los sumandos
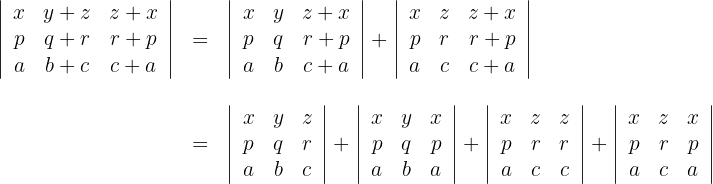
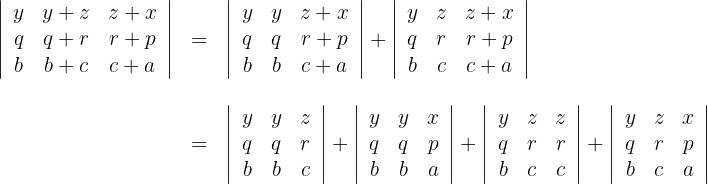
3Si se tienen dos columnas iguales, entonces el determinante es cero, por lo que tenemos
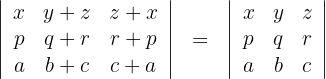
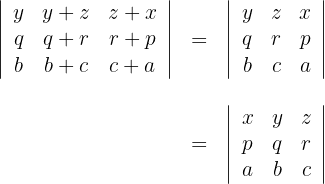
4De esta forma se verifica que se cumple
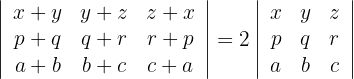
Segunda igualdad
1Multiplicamos la primera fila por  , la segunda fila por
, la segunda fila por  y la tercera fila por , por lo que par mantenerla igualdad tenemos que multiplicar por
y la tercera fila por , por lo que par mantenerla igualdad tenemos que multiplicar por 
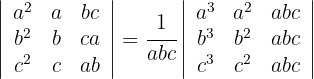
2La tercera columna tiene un factor en común
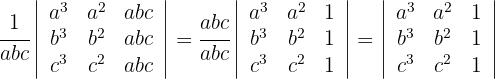
Resolver las siguientes ecuaciones sin desarrollar los determinantes.
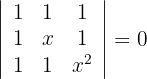
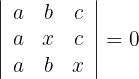
Primera ecuación
1Reemplazamos las filas  por
por 
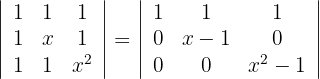
2La matriz es triangular por lo que el determinante es igual al producto de su diagonal
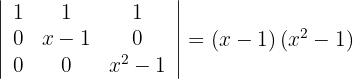
3Como el determinante es igual a cero, se obtienen que 
Segunda ecuación
1La primera columna tiene un factor en común
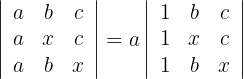
2Reemplazamos las filas 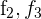 por
por 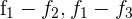
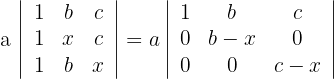
3La matriz es triangular por lo que el determinante es igual al producto de su diagonal
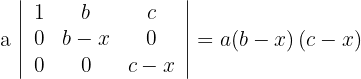
4Como el determinante es igual a cero, se obtienen que 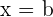 y
y 
Hallar la matriz inversa de:
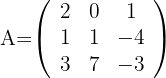
1Calculamos el determinante
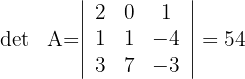
2Calculamos la matriz adjunta
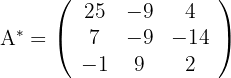
3Calculamos su transpuesta
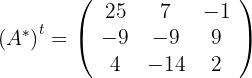
4La inversa viene dada por 
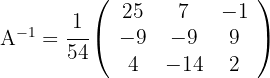
¿Para qué valores de  la matriz
la matriz
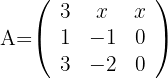
no admite matriz inversa?
1Calculamos el determinante reduciendo los cálculos a partir de la tercera columna
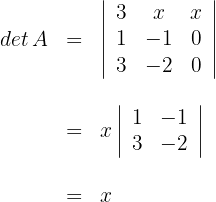
2Una matriz no posee inversa si su determinante es cero. Así, la matriz  no tiene inversa cuando
no tiene inversa cuando 
¿Para qué valores de  la matriz
la matriz
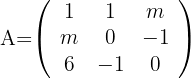
no admite matriz inversa?
1Calculamos el determinante
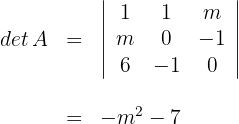
2Una matriz no posee inversa si su determinante es cero. El determinante 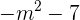 siempre es negativo para cualquier valor real de
siempre es negativo para cualquier valor real de  . Así, la matriz
. Así, la matriz  siempre posee inversa, independientemente del valor real de
siempre posee inversa, independientemente del valor real de 
Calcular el rango de las siguientes matrices:
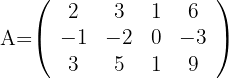
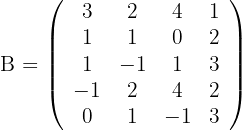

Rango de 
1Calculamos los determinantes de las submatrices de rango 1
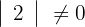
2Calculamos los determinantes de las submatrices de rango 2
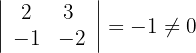
3Calculamos los determinantes de las submatrices de rango 3
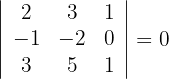
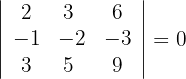
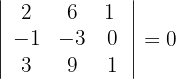
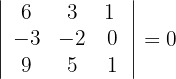
4Así, el rango de la matriz es 2
Rango de 
1Calculamos los determinantes de las submatrices de rango 1
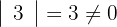
2Calculamos los determinantes de las submatrices de rango 2
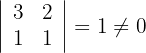
3Calculamos los determinantes de las submatrices de rango 3
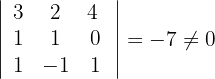
4Calculamos los determinantes de las submatrices de rango 4
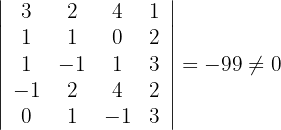
5Así, el rango de la matriz es 4
Rango de 
1Eliminamos la tercera columna por ser nula, la cuarta por ser proporcional a la primera, y la quinta porque combinación lineal de la primera y segunda 

2Calculamos los determinantes de las submatrices de rango 1
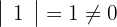
3Calculamos los determinantes de las submatrices de rango 2
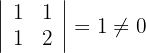
4Así, el rango de la matriz es 2
Resolver las siguientes ecuaciones matriciales:
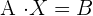
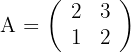
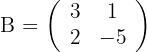
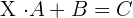
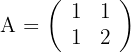
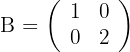
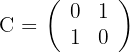
Primera ecuación
1El determinante de  es distinto de cero, por lo que existe su inversa
es distinto de cero, por lo que existe su inversa
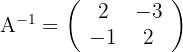
2Resolvemos la ecuación
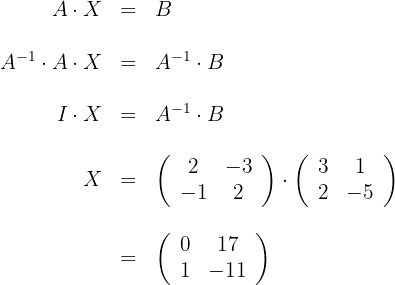
Segunda ecuación
1El determinante de  es distinto de cero, por lo que existe su inversa
es distinto de cero, por lo que existe su inversa
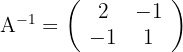
2Resolvemos la ecuación
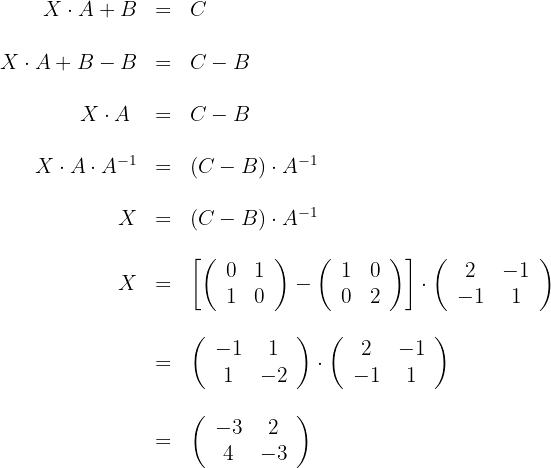
Resolver la ecuación matricial:

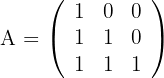

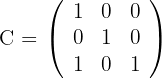
1El determinante de  es distinto de cero, por lo que existe su inversa
es distinto de cero, por lo que existe su inversa
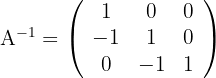
2Resolvemos la ecuación
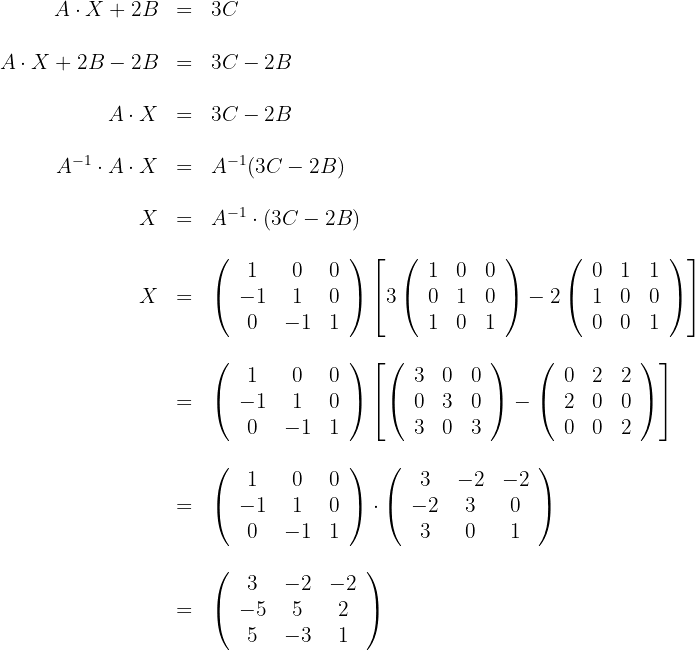
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
ME PUEDEN DAR LA AUTORA Y EL AÑO EN QUE SE PUBLICO
¡Hola Luis! 👋 Desde Superprof nos alegra que el artículo te sea útil. 😊 Para citarlo, puedes usar la siguiente referencia:
«Superprof. Ejercicios de determinantes II. [En línea] Disponible en: [URL del artículo].»
Por privacidad, no podemos facilitar el nombre completo del autor ni la fecha exacta de publicación, pero esta forma permite que tu cita sea válida en trabajos académicos. 📚✨
Falta la propiedad de la inversa de una matriz= 1/ la matriz
Hola, si tenemos un artículo con el tema de la inversa de una matriz es este «https://www.superprof.es/apuntes/escolar/matematicas/algebralineal/matrices/formulas-de-matriz-inversa.html».
Hola. Una sugerencia:
En el aparte 5, sugiero añadir algo a la explicación de la regla de invariancia citada previamente.
La original dice: «Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.»
La sugerencia sería: «Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás y de ella misma, el valor del determinante no varía.»
Espero que eso ayude…
Gracias por estar ahí… Saludos!!
Buenos días.
Si en el ejemplo del punto 5 anterior hacemos la siguiente transformación
C3=2C1+C2-C3
el determinante resultante cambia de signo (para a valer -16).
Y esto sería otra combinación lineal en la que se incluye a la propia columna 3…
Fijate que me aparece el articulo «Ejercicios de determinantes II» y no encuentro lo que mencionas, podrias indicarme el articulo que mencionas, gracias por la sugerencia.
Colo resolver el método de determinante de
5×-2y=1
3×+y=5
(1-1 0 0 2 1 1 3 -1