Bienvenidos a nuestra página dedicada a los Ejercicios y Aplicaciones de la Distribución Binomial. La distribución binomial es una herramienta fundamental en la teoría de la probabilidad y se utiliza para modelar eventos que pueden tener dos resultados posibles, como éxito o fracaso, sí o no. En esta guía, les guiaremos a través de una serie de ejercicios y aplicaciones que exploran esta distribución y su relevancia en diversos contextos.
La distribución binomial se caracteriza por la probabilidad de éxito en cada ensayo, el número total de ensayos y el interés en contar cuántos éxitos ocurren en una serie de ensayos independientes. A lo largo de esta guía, aprenderemos a aplicar la distribución binomial para calcular probabilidades de eventos, como el número de éxitos en un número determinado de ensayos o la probabilidad de que ocurra un evento específico en un cierto número de repeticiones.
Se lanza una moneda cuatro veces. Calcular la probabilidad de que salgan más caras que cruces.
Al lanzar una moneda la probabilidad de que salga cara es 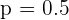 y de que salga cruz es
y de que salga cruz es  . En este caso, el experimento de lanzar se realizará cuatro veces, así,
. En este caso, el experimento de lanzar se realizará cuatro veces, así,  . Por lo tanto, tenemos la distribución binomial
. Por lo tanto, tenemos la distribución binomial 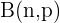 con los siguientes parámetros:
con los siguientes parámetros:

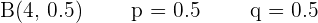
Ahora, como deseamos conocer la probabilidad de que salgan más caras que cruces, los eventos donde esto ocurre es cuando, o salen tres caras y una cruz, o salen cuatro caras y cero cruces, por lo que,
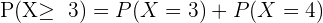
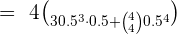

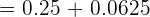
 { = 0.3125}[/latex
{ = 0.3125}[/latex
Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en estas condiciones viva  años o más es
años o más es  . Hállese la probabilidad de que, transcurridos
. Hállese la probabilidad de que, transcurridos  años, vivan:
años, vivan:
a Las cinco personas.
b Al menos tres personas.
c Exactamente dos personas.
Tomemos en cuenta la distribución binomial 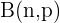 con los siguientes parámetros:
con los siguientes parámetros:
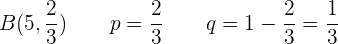
aLas cinco personas.
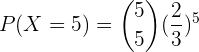
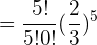
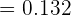
bAl menos tres personas.
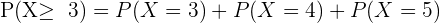

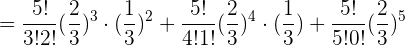
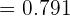
cExactamente dos personas.
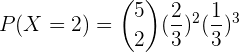
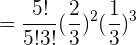
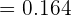
Si de seis a siete de la tarde se admite que un número de teléfono de cada cinco está comunicando, ¿cuál es la probabilidad de que, cuando se marquen  números de teléfono elegidos al azar, sólo comuniquen dos?
números de teléfono elegidos al azar, sólo comuniquen dos?
Tomemos en cuenta la distribución binomial 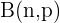 con los siguientes parámetros:
con los siguientes parámetros:
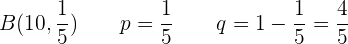
Calculemos la probabilidad deque cuando se marquen  números de teléfono sólo comuniquen dos.
números de teléfono sólo comuniquen dos.
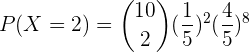
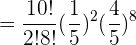

La probabilidad de que un hombre acierte en el blanco es 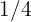 . Si dispara
. Si dispara  veces.
veces.
a ¿Cuál es la probabilidad de que acierte exactamente en tres ocasiones?
b ¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
Tomemos en cuenta la distribución binomial 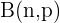 con los siguientes parámetros:
con los siguientes parámetros:
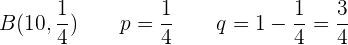
a ¿Cuál es la probabilidad de que acierte exactamente en tres ocasiones?
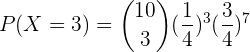
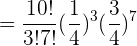

b¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
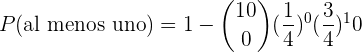


En una urna hay  bolas,
bolas,  rojas y el resto blancas. Se elige una bola al azar y se anota si es roja; el proceso se repite, devolviendo la bola,
rojas y el resto blancas. Se elige una bola al azar y se anota si es roja; el proceso se repite, devolviendo la bola,  veces. Calcular la media y la desviación típica
veces. Calcular la media y la desviación típica
Tomemos en cuenta la distribución binomial 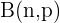 con los siguientes parámetros:
con los siguientes parámetros:
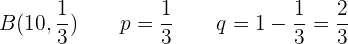
Media:
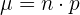
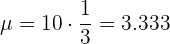
Desviación típica:

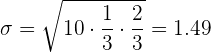
En unas pruebas de alcoholemia se ha observado que el  de los conductores controlados dan positivo en la prueba y que el
de los conductores controlados dan positivo en la prueba y que el 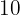 de los conductores controlados no llevan puesto el cinturón de seguridad. También se ha observado que las dos infracciones son independientes. Un guardia de tráfico para cinco conductores al azar. Si tenemos en cuenta que el número de conductores es suficientemente importante como para estimar que la proporción de infractores no varía al hacer la selección
de los conductores controlados no llevan puesto el cinturón de seguridad. También se ha observado que las dos infracciones son independientes. Un guardia de tráfico para cinco conductores al azar. Si tenemos en cuenta que el número de conductores es suficientemente importante como para estimar que la proporción de infractores no varía al hacer la selección
a Determinar la probabilidad de que exactamente tres conductores hayan cometido alguna de las dos infracciones.
b Determine la probabilidad de que al menos uno de los conductores controlados haya cometido alguna de las dos infracciones.
Definamos los siguientes eventos:
A: Los conductores dan positivo a la prueba de alcoholemia.
B: Los conductores no llevan puesto el cinturón de seguridad.
Luego, la probabilidad de que el conductor de positivo a la prueba o de que no lleve su cinturón de seguridad o de que ambos eventos ocurran, conociendo que las infracciones son independientes es: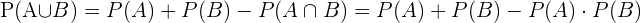
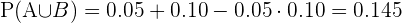
Ahora, tomemos en cuenta la distribución binomial B(n,p) con los siguientes parámetros:

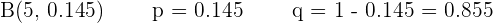
aDeterminar la probabilidad de que exactamente tres conductores hayan cometido alguna de las dos infracciones.
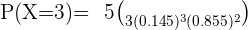
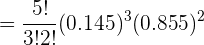
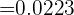
bDetermine la probabilidad de que al menos uno de los conductores controlados haya cometido alguna de las dos infracciones.
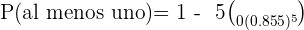

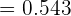
Un laboratorio afirma que una droga causa efectos secundarios en una proporción de  de cada
de cada  pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a
pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a  pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?
pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?
a Ningún paciente tenga efectos secundarios.
b Al menos dos tengan efectos secundarios.
c ¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige  pacientes al azar?
pacientes al azar?
Tomemos en cuenta la distribución binomial B(n,p) con los siguientes parámetros:
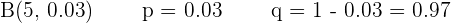
aNingún paciente tenga efectos secundarios.
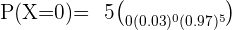
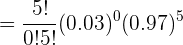
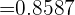
bAl menos dos tengan efectos secundarios.
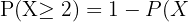

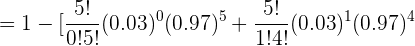

c¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige 100 pacientes al azar?
Media:
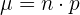
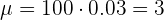
Un equipo de béisbol con un promedio de bateo del 0.300 (30% de éxito) realiza 10 ensayos independientes. ¿Cuál es la probabilidad de que anoten al menos 5 carreras en cada uno de esos ensayos?
La probabilidad de que ocurran al menos 5 veces está dado por
Entonces, calculamos cada una de estas probabilidades utilizando la distribución binomial con  y
y  .
.
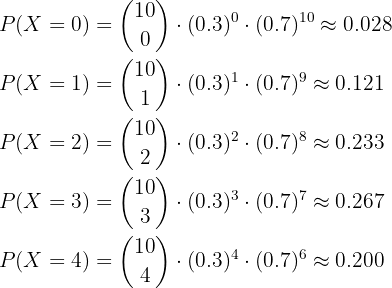
Es decir, 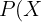
Supongamos que tienes una moneda y quieres calcular cuántos lanzamientos necesitas para que la probabilidad de obtener al menos 3 caras sea igual o mayor al 90%. Sabes que la probabilidad de obtener una cara en un solo lanzamiento es del 50% (0.5).
a ¿Cuántos lanzamientos de la moneda se necesitan para tener al menos un 90% de probabilidad de obtener al menos 3 caras?
b ¿Cuál es la probabilidad de obtener al menos 3 caras en ese número de lanzamientos?
a
Queremos encontrar un número  que nos permita tener
que nos permita tener 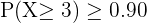 . Para obtener tal número, debemos calcular la probabilidad de cada uno de estos escenarios con al menos 3 lanzamientos, hasta encontrar uno que satisfaga la condición. Primero, podemos escribir la función de distribución con el
. Para obtener tal número, debemos calcular la probabilidad de cada uno de estos escenarios con al menos 3 lanzamientos, hasta encontrar uno que satisfaga la condición. Primero, podemos escribir la función de distribución con el  que buscamos:
que buscamos:
Entonces, sustituyendo a  (el número de ensayos) con valores enteros mayores a 3 y calculando el resultado, conseguimos los siguientes valores:
(el número de ensayos) con valores enteros mayores a 3 y calculando el resultado, conseguimos los siguientes valores:
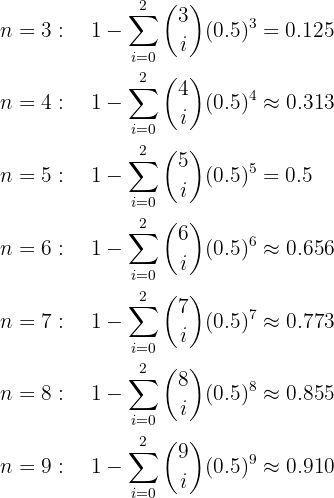
Entonces, necesitamos al menos 9 ensayos para que nuestro experimento tenga un mínimo de 3 caras.
b
Calculado de la misma manera que en inciso anterior, tenemos que la probabilidad de obtener 3 caras en 9 ensayos tiene una probabilidad de
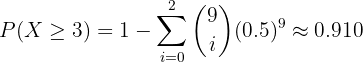
En un concurso de preguntas de opción múltiple, cada pregunta tiene 5 opciones de respuesta y solo una es correcta. Un estudiante decide responder al azar a todas las preguntas del concurso, que consta de 20 preguntas.
a ¿Cuál es la probabilidad de que el estudiante responda correctamente exactamente 9 preguntas?
b Calcula la media y la varianza.
a
Teniendo 5 opciones en cada pregunta, tenemos una probabilidad de 0.2 de acertar si elegimos al azar. Entonces, la probabilidad de obtener exactamente 9 aciertos es dada por
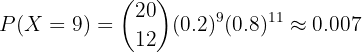
b
Recordemos que la media es dada por
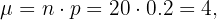
donde 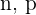 son el número de ensayos y la probabilidad del evento, respectivamente. La varianza es dada por
son el número de ensayos y la probabilidad del evento, respectivamente. La varianza es dada por
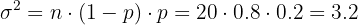
Es decir, en promedio, un estudiante que conteste 20 preguntas al azar, obtendrá 4 aciertos.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el cálculo de la varianza, en el ejemplo, es incorrecto: al sumatorio de Xi2xPi falta restarle el cuadrado de la esperanza.
Será error de imprenta, porque el resultado 2,92 sí que es correcto
Hola, lo que pasa es que se aplica otra fórmula para resolver el ejercicio, por eso incluso si da el resultado correcto, eso sucede muy a menudo en fórmulas de estadística.
Hola profe una pregunta me puedes ayydar con este ejerccicio no lo he entendido bien
Una moneda equulibrada se lanza 5 veces calcula la probabilidad de obtener
A) exactamente 3 caras
B) como maximo 2 caras
Se realizó una investigación sobre el desempeño docente de la EIB en los colegios privados
del distrito de San Juan de Lurigancho, se ha tomado una muestra de 54 docente. Se ha
escogido las edades de los docentes para el análisis, otras variables indican que los docentes
jóvenes (X<29 años) presenta mayor desempeño en las aulas, como resultado los logros de
los estudiantes han mejorado con relación al año pasado. De la información de la tabla, esta
conformada por la frecuencia de las edades, porcentaje, porcentaje validos (se refiere a los
datos perdido) y el porcentaje acumulado. hallar la esperanza matemática y la varianza para
la población joven y distintos a ellos. ¿Qué puede inferir con esos datos hallados? ¿Qué
acciones tomaría para mejorar el desempeño y el logro de los estudiantes? y finalmente
¿Cuál es la probabilidad de docentes entre 29 a 31 años?
En un estudio sobre comportamiento de compras, se observa que el 40% de los clientes, prefieren realizar compras en línea, si se seleccionan 10 clientes al azar, determina el porcentaje de que al menos seis prefieran comprar en línea:
buenos dias me puede decir que tipo de problema de probabilidad es el siguiente: en un grupo de matematicas el 80.5% de los alumnos acreditan la materia. si se toma una muestra de 100 alumnos calcular la probabilidad de que: a) mas del 88% acrediten la materia b) entre el 85 y el 90% acrediten la materia c)mas del 72% acrediten la materia d) menos del 80.5 acrediten la materia e) entre 71 y el 76% acrediten la materia f) menos del 75% acrediten la materia g) entre el 78 y el 84 % acrediten la materia h) menos del 90% acrediten la materia. Me puede orientar por favor
Dos jóvenes hacen una apuesta, el primero apuesta al segundo que en 5 intentos de valado al ambos obtienen 2 soles.
A) ¿Quien tiene la mayor probabilidad de ganar?
(p)=0,7
¿Y si te preguntan la probabilidad de que ocurra algo?