Un jugador lanza dos monedas. Gana  ó
ó  € si aparecen una o dos caras. Por otra parte pierde
€ si aparecen una o dos caras. Por otra parte pierde  € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable
€ si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable
Primero consideremos el espacio muestral, este corresponde al conjunto de posibles resultados al lanzar las monedas.
Si denotamos  al hecho de obtener cara y por
al hecho de obtener cara y por  al hecho de no obtener cara. Podemos decir que nuestro espacio muestral es
al hecho de no obtener cara. Podemos decir que nuestro espacio muestral es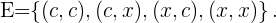
Estos vectores representan lo que obtuve en cada una de las monedas, por ejemplo 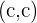 nos dice que obtuve dos caras al lanzar las monedas.
nos dice que obtuve dos caras al lanzar las monedas.
Ahora calculamos las probabilidades de ganar o perder.
La probabilidad de ganar un euro es igual al numero de posibles casos favorables sobre el numero de todos los casos posibles que en este caso siempre es  .
.
Los casos donde obtengo una cara son  y
y  , es decir, hay dos casos posibles, entonces la probabilidad es
, es decir, hay dos casos posibles, entonces la probabilidad es 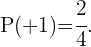
Similarmente, dado que solo hay un caso donde obtengo dos cara, 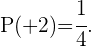
De igual forma, solo hay un caso donde no obtengo caras, es decir, pierdo  euros, entonces
euros, entonces 
Finalmente, recordemos que la esperanza no es mas que la suma de los productos de las probabilidades de un suceso por el valor del suceso, así 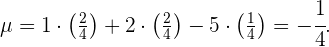 Por lo tanto concluimos que la esperanza es desfavorable.
Por lo tanto concluimos que la esperanza es desfavorable.
Dada la función:
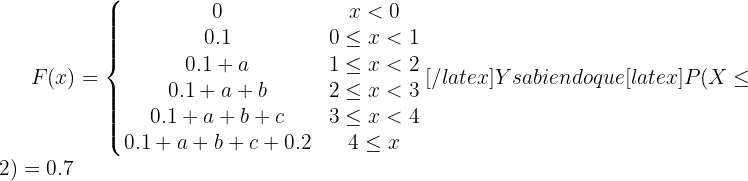 y
y 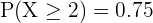 , hallar:
, hallar:
A La esperanza matemática
B La varianza
C La desviación típica
Primero debemos encontrar el valor de las incógnitas  ,
,  y
y  . Para esto, primero utilizamos:
. Para esto, primero utilizamos:
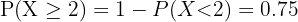
Notamos que esto es equivalente a calcular

Luego, sustituyendo el valor de  en
en

Tenemos que 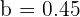 . Por último, tenemos que:
. Por último, tenemos que:
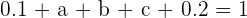
de donde se sigue que 
Observemos que  es la función de distribución (probabilidad acumulada). A partir de aquí podemos obtener la función de probabilidad, la cual es
es la función de distribución (probabilidad acumulada). A partir de aquí podemos obtener la función de probabilidad, la cual es
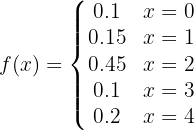
Con esto ya podemos encontrar lo que se nos pide:
 | 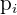 | 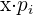 |  |
|---|---|---|---|
| 0 | 0.1 | 0 | 0 |
| 1 | 0.15 | 0.15 | 0.15 |
| 2 | 0.45 | 0.9 | 1.8 |
| 3 | 0.1 | 0.3 | 0.9 |
| 4 | 0.2 | 0.8 | 3.2 |
| 2.15 | 6.05 |
ALa esperanza matemática 
BLa varianza 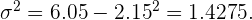
CLa desviación típica 
Se venden 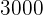 boletos para una rifa a
boletos para una rifa a  euro cada uno. Si el único premio del sorteo es de
euro cada uno. Si el único premio del sorteo es de 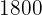 euros, calcular el resultado que debe esperar una persona que compra
euros, calcular el resultado que debe esperar una persona que compra  billetes.
billetes.
Consideramos la variable discreta
Los posibles valores para  son:
son: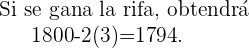
Y tendremos que la probabilidad es 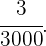
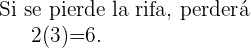 Y tendremos que la probabilidad es
Y tendremos que la probabilidad es 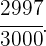
De esta forma el resultado que una persona debe si compra  billetes es
billetes es 
Una variable discreta tiene la siguiente función de densidad entre  y
y  :
: 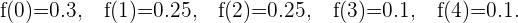
Calcular su esperanza y varianza.
La esperanza matemática de la variable viene dada por

La varianza viene dada por  .
.
Calculamos la esperanza de la variable 
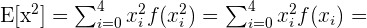
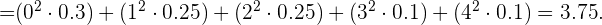
Por lo tanto 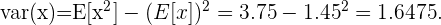
Se lanza un dado equilibrado produciendo el espacio 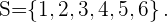 la variable aleatoria
la variable aleatoria  representa el doble del número que aparece. Encuentra la esperanza y la varianza.
representa el doble del número que aparece. Encuentra la esperanza y la varianza.
Dada la descripción para  tenemos que
tenemos que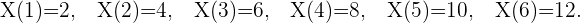
Por lo tanto  tiene la siguiente función distribución
tiene la siguiente función distribución 
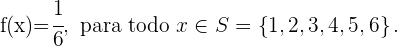
Concluimos que la esperanza esta dada por 
Ademas, 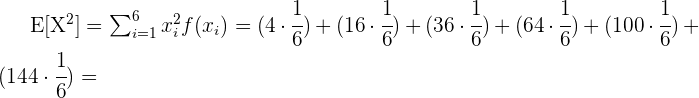

Finalmente la varianza  esta dada por
esta dada por 
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el cálculo de la varianza, en el ejemplo, es incorrecto: al sumatorio de Xi2xPi falta restarle el cuadrado de la esperanza.
Será error de imprenta, porque el resultado 2,92 sí que es correcto
Hola, lo que pasa es que se aplica otra fórmula para resolver el ejercicio, por eso incluso si da el resultado correcto, eso sucede muy a menudo en fórmulas de estadística.
Hola profe una pregunta me puedes ayydar con este ejerccicio no lo he entendido bien
Una moneda equulibrada se lanza 5 veces calcula la probabilidad de obtener
A) exactamente 3 caras
B) como maximo 2 caras
Se realizó una investigación sobre el desempeño docente de la EIB en los colegios privados
del distrito de San Juan de Lurigancho, se ha tomado una muestra de 54 docente. Se ha
escogido las edades de los docentes para el análisis, otras variables indican que los docentes
jóvenes (X<29 años) presenta mayor desempeño en las aulas, como resultado los logros de
los estudiantes han mejorado con relación al año pasado. De la información de la tabla, esta
conformada por la frecuencia de las edades, porcentaje, porcentaje validos (se refiere a los
datos perdido) y el porcentaje acumulado. hallar la esperanza matemática y la varianza para
la población joven y distintos a ellos. ¿Qué puede inferir con esos datos hallados? ¿Qué
acciones tomaría para mejorar el desempeño y el logro de los estudiantes? y finalmente
¿Cuál es la probabilidad de docentes entre 29 a 31 años?
En un estudio sobre comportamiento de compras, se observa que el 40% de los clientes, prefieren realizar compras en línea, si se seleccionan 10 clientes al azar, determina el porcentaje de que al menos seis prefieran comprar en línea:
buenos dias me puede decir que tipo de problema de probabilidad es el siguiente: en un grupo de matematicas el 80.5% de los alumnos acreditan la materia. si se toma una muestra de 100 alumnos calcular la probabilidad de que: a) mas del 88% acrediten la materia b) entre el 85 y el 90% acrediten la materia c)mas del 72% acrediten la materia d) menos del 80.5 acrediten la materia e) entre 71 y el 76% acrediten la materia f) menos del 75% acrediten la materia g) entre el 78 y el 84 % acrediten la materia h) menos del 90% acrediten la materia. Me puede orientar por favor
Dos jóvenes hacen una apuesta, el primero apuesta al segundo que en 5 intentos de valado al ambos obtienen 2 soles.
A) ¿Quien tiene la mayor probabilidad de ganar?
(p)=0,7
¿Y si te preguntan la probabilidad de que ocurra algo?