Una variable aleatoria discreta es aquella que toma unicamente valores discretos o aislados, mientras que una variable aleatoria continua es aquella que toma valores de un intervalo.
Ejemplo:
La variable que asigna el número de autos vendidos en una agencia automotriz es una variable discreta que puede tomar los valores 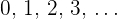 .
.
Ejemplo:
La variable que asigna la temperatura en una ciudad es una variable continua que puede tomar los valores  , donde
, donde  y
y  representan la temperatura mínima y máxima respectivamente que se alcanza en un día.
representan la temperatura mínima y máxima respectivamente que se alcanza en un día.

Esperanza matemática o media
Es una medida de tendencia central que se emplea para designar mediante un solo valor a una colección de elementos y se representa por 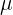

Varianza
Es una medida de dispersión que se emplea para indicar que tan cercanos de la media se encuentran los elementos de la colección y se representa por 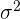 . Si la varianza es cero, entonces los elementos coinciden con la media; mientras mayor sea la varianza, mayor dipersión.
. Si la varianza es cero, entonces los elementos coinciden con la media; mientras mayor sea la varianza, mayor dipersión.
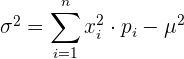
Desviación típica
Es una medida de dispersión que se emplea para indicar que tan cercanos de la media se encuentran los elementos de la colección y se representa por  . Si la desviación estándar es cero, entonces los elementos coinciden con la media; mientras mayor sea la desviación estándar, mayor dipersión.
. Si la desviación estándar es cero, entonces los elementos coinciden con la media; mientras mayor sea la desviación estándar, mayor dipersión.

Distribución binomial
Es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de  ensayos independientes entre sí, con una probabilidad de éxito
ensayos independientes entre sí, con una probabilidad de éxito 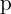
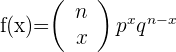
 es el número de pruebas.
es el número de pruebas.
 es el número de éxitos.
es el número de éxitos.
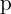 es la probabilidad de éxito.
es la probabilidad de éxito.
 es la probabilidad de fracaso.
es la probabilidad de fracaso.
 es el número combinatorio.
es el número combinatorio.
Ejemplo:
Calcular la esperanza matemática, la varianza, y la desviación típica, de la distribución de probabilidad de las puntuaciones obtenidas al lanzar un dado.
 | 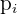 |  | 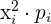 |
|---|---|---|---|
| 1 |  |  |  |
| 2 |  |  |  |
| 3 |  |  |  |
| 4 |  |  | 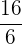 |
| 5 |  |  |  |
| 6 |  | 1 | 6 |
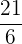 | 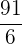 |
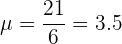
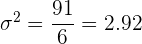

Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el cálculo de la varianza, en el ejemplo, es incorrecto: al sumatorio de Xi2xPi falta restarle el cuadrado de la esperanza.
Será error de imprenta, porque el resultado 2,92 sí que es correcto
Hola, lo que pasa es que se aplica otra fórmula para resolver el ejercicio, por eso incluso si da el resultado correcto, eso sucede muy a menudo en fórmulas de estadística.
Hola profe una pregunta me puedes ayydar con este ejerccicio no lo he entendido bien
Una moneda equulibrada se lanza 5 veces calcula la probabilidad de obtener
A) exactamente 3 caras
B) como maximo 2 caras
Se realizó una investigación sobre el desempeño docente de la EIB en los colegios privados
del distrito de San Juan de Lurigancho, se ha tomado una muestra de 54 docente. Se ha
escogido las edades de los docentes para el análisis, otras variables indican que los docentes
jóvenes (X<29 años) presenta mayor desempeño en las aulas, como resultado los logros de
los estudiantes han mejorado con relación al año pasado. De la información de la tabla, esta
conformada por la frecuencia de las edades, porcentaje, porcentaje validos (se refiere a los
datos perdido) y el porcentaje acumulado. hallar la esperanza matemática y la varianza para
la población joven y distintos a ellos. ¿Qué puede inferir con esos datos hallados? ¿Qué
acciones tomaría para mejorar el desempeño y el logro de los estudiantes? y finalmente
¿Cuál es la probabilidad de docentes entre 29 a 31 años?
En un estudio sobre comportamiento de compras, se observa que el 40% de los clientes, prefieren realizar compras en línea, si se seleccionan 10 clientes al azar, determina el porcentaje de que al menos seis prefieran comprar en línea:
buenos dias me puede decir que tipo de problema de probabilidad es el siguiente: en un grupo de matematicas el 80.5% de los alumnos acreditan la materia. si se toma una muestra de 100 alumnos calcular la probabilidad de que: a) mas del 88% acrediten la materia b) entre el 85 y el 90% acrediten la materia c)mas del 72% acrediten la materia d) menos del 80.5 acrediten la materia e) entre 71 y el 76% acrediten la materia f) menos del 75% acrediten la materia g) entre el 78 y el 84 % acrediten la materia h) menos del 90% acrediten la materia. Me puede orientar por favor
Dos jóvenes hacen una apuesta, el primero apuesta al segundo que en 5 intentos de valado al ambos obtienen 2 soles.
A) ¿Quien tiene la mayor probabilidad de ganar?
(p)=0,7
¿Y si te preguntan la probabilidad de que ocurra algo?