La distribución binomial es uno de los modelos más importantes en la estadística y se utiliza para describir fenómenos en los que hay dos posibles resultados en cada ensayo, como éxito o fracaso. Esta distribución es especialmente útil en situaciones donde se repiten experimentos independientes, como el lanzamiento de una moneda o el examen de la efectividad de un tratamiento médico. En este contexto, los ejercicios resueltos de distribución binomial permiten ilustrar cómo calcular probabilidades y otros parámetros clave, como la media y la varianza, en situaciones prácticas. A través de estos ejemplos, se busca facilitar la comprensión de los principios fundamentales de la distribución binomial y su aplicación en la resolución de problemas estadísticos.
Un distribuidor de berries observa que de cada diez fresas una no se encuentra en excelente estado. ¿Cuál es la probabilidad de que de 15 fresas, ninguna se encuentre en mal estado?
Un distribuidor de berries observa que de cada diez fresas una no se encuentra en excelente estado.
La probabilidad de que de 15 fresas, ninguna se encuentre en mal estado es:
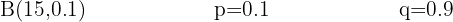
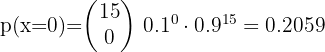
Una persona tiene 0.7 de probabilidad de responder correctamente una pregunta. ¿Cuál es la probabilidad de que de 10 preguntas, responda todas correctamente?
Una persona tiene 0.7 de probabilidad de responder correctamente una pregunta..
La probabilidad de que de 10 preguntas, responda correctamente todas es:
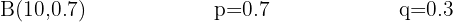
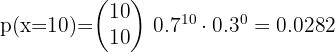
Se lanza un dado dos veces. ¿Cuál es la probabilidad de obtener dos números pares?
Se lanza un dado dos veces.
La probabilidad de obtener dos números pares es:
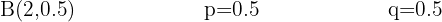
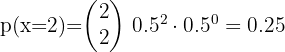
Un jugador de futbol un gol de cada 9 tiros a la portería contraria. Si realiza 15 disparos a la portería del equipo rival, ¿cuál es la probabilidad de que anote dos goles?
Un jugador de futbol un gol de cada 9 tiros a la portería contraria.
La probabilidad de que anote dos goles es:
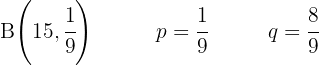
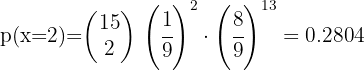
Un jugador de baloncesto acierta 5 de cada 8 tiros a la canasta. Si en un partido lanza 10 veces al aro, ¿cuál es la probabilidad de encestar en 6 ocasiones?
Un jugador de baloncesto acierta 5 de cada 8 tiros a la canasta.
La probabilidad de que de enceste seis veces es:
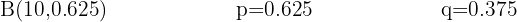
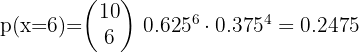
Un agricultor observa que de cada 10 plantas una se enferma. ¿Cuál es la probabilidad de que de 12 plantas, se enfermen 2?
Un agricultor observa que de cada 10 plantas una se enferma.
La probabilidad de que de 12 plantas, se enfermen 2 es:
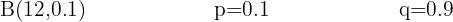
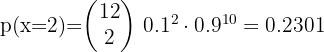
La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leído. Un grupo de 4 amigos son aficionados a la lectura:
1 ¿Cuál es la probabilidad de que en el grupo hayan leído la novela 2 personas?
2 ¿Y cómo máximo 2?
La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leído. Un grupo de 4 amigos son aficionados a la lectura:
1¿Cuál es la probabilidad de que en el grupo hayan leído la novela 2 personas?
2¿Y cómo máximo 2?
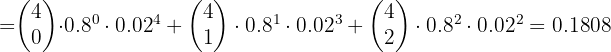
Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en estas condiciones viva 30 años o más es 2/3. Hállese la probabilidad de que, transcurridos 30 años, vivan:
1 Las cinco personas
2 Al menos tres personas
3 Exactamente dos personas
Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en estas
condiciones viva 30 años o más es 
. Hállese la probabilidad de que, transcurridos 30 años, vivan:
1 Las cinco personas
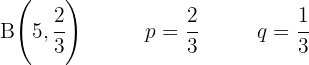
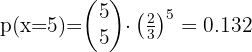
2 Al menos tres personas
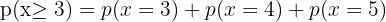
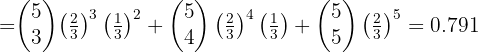
3 Exactamente dos personas
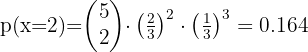
Se lanza una moneda cuatro veces. Calcular la probabilidad de que salgan más caras que cruces.
Se lanza una moneda cuatro veces. Calcular la probabilidad de que salgan más caras que cruces.
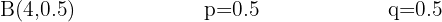
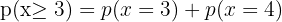
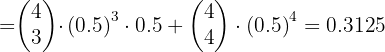
Si de seis a siete de la tarde se admite que un número de teléfono de cada cinco está comunicando. ¿Cuál es la probabilidad de que, cuando se marquen 10 números de
teléfono elegidos al azar, sólo comuniquen dos?
Si de seis a siete de la tarde se admite que un número de teléfono de cada cinco está comunicando. ¿Cuál es la probabilidad de que, cuando se marquen 10 números de teléfono elegidos al azar, sólo comuniquen dos?
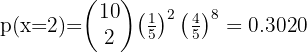
La probabilidad de que un hombre acierte en el blanco es 1/4. Si dispara 10 veces
1 ¿Cuál es la probabilidad de que acierte exactamente en tres ocasiones?
2 ¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
La probabilidad de que un hombre acierte en el blanco es 
. Si dispara 10 veces
1 ¿Cuál es la probabilidad de que acierte exactamente en tres ocasiones?
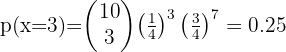
2 ¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
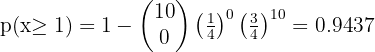
En unas pruebas de alcoholemia se ha observado que el 5% de los conductores controlados dan positivo en la prueba y que el 10% de los conductores controlados no llevan puesto el cinturón de seguridad. También se ha observado que las dos infracciones son independientes.
Un guardia de tráfico para cinco conductores al azar. Si tenemos en cuenta que el número de conductores es suficientemente importante como para estimar que la proporción de infractores no varía al hacer la selección.
1 Determinar la probabilidad de que exactamente tres conductores hayan cometido alguna de las dos infracciones.
2 Determine la probabilidad de que al menos uno de los conductores controlados haya cometido alguna de las dos infracciones.
En unas pruebas de alcoholemia se ha observado que el 5% de los conductores controlados dan positivo en la prueba y que el 10% de los conductores controlados no llevan puesto el cinturón de seguridad. También se ha observado que las dos infracciones son independientes.
Un guardia de tráfico para cinco conductores al azar. Si tenemos en cuenta que el número de conductores es suficientemente importante como para estimar que la proporción de infractores no varía al hacer la selección.
1 Determinar la probabilidad de que exactamente tres conductores hayan cometido alguna de las dos infracciones.
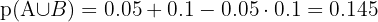
2 Determine la probabilidad de que al menos uno de los conductores controlados haya cometido alguna de las dos infracciones.
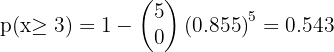
La probabilidad de que un artículo producido por una fabrica sea defectuoso es p = 0.02. Se envió un cargamento de 10.000 artículos a unos almacenes. Hallar el número esperado de artículos defectuosos, la varianza y la desviación típica.
La probabilidad de que un artículo producido por una fabrica sea defectuoso es p = 0.02. Se envió un cargamento de 10.000 artículos a unos almacenes. Hallar el número esperado de artículos defectuosos, la varianza y la desviación típica.
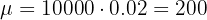
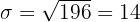
En una urna hay 30 bolas, 10 rojas y el resto blancas. Se elige una bola al azar y se anota si es roja; el proceso se repite, devolviendo la bola, 10 veces. Calcular la media y la desviación típica.
En una urna hay 30 bolas, 10 rojas y el resto blancas. Se elige una bola al azar y se anota si es roja; el proceso se repite, devolviendo la bola, 10 veces. Calcular la media y la desviación típica.
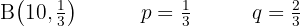
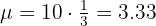
Un laboratorio afirma que una droga causa efectos secundarios en una proporción de 3 de cada 100 pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a 5 pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?
1 Ningún paciente tenga efectos secundarios
2 Al menos dos tengan efectos secundarios
3 ¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige 100 pacientes al azar?
Un laboratorio afirma que una droga causa efectos secundarios en una proporción de 3 de cada 100 pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a 5 pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?
1 Ningún paciente tenga efectos secundarios
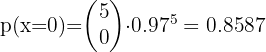
2 Al menos dos tengan efectos secundarios
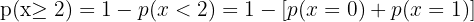
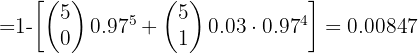
3 ¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige 100 pacientes al azar?
Si eres de los que prefieres un profesor de mates, no dudes en echar un vistazo a todos los que están deseando darte clases a través de Superprof. ¿Que prefieres un profesor de matematicas online? ¡También tenemos profes que ofrecen clases a distancia!
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola profe una pregunta me puedes ayydar con este ejerccicio no lo he entendido bien
Una moneda equulibrada se lanza 5 veces calcula la probabilidad de obtener
A) exactamente 3 caras
B) como maximo 2 caras
Se realizó una investigación sobre el desempeño docente de la EIB en los colegios privados
del distrito de San Juan de Lurigancho, se ha tomado una muestra de 54 docente. Se ha
escogido las edades de los docentes para el análisis, otras variables indican que los docentes
jóvenes (X<29 años) presenta mayor desempeño en las aulas, como resultado los logros de
los estudiantes han mejorado con relación al año pasado. De la información de la tabla, esta
conformada por la frecuencia de las edades, porcentaje, porcentaje validos (se refiere a los
datos perdido) y el porcentaje acumulado. hallar la esperanza matemática y la varianza para
la población joven y distintos a ellos. ¿Qué puede inferir con esos datos hallados? ¿Qué
acciones tomaría para mejorar el desempeño y el logro de los estudiantes? y finalmente
¿Cuál es la probabilidad de docentes entre 29 a 31 años?
En un estudio sobre comportamiento de compras, se observa que el 40% de los clientes, prefieren realizar compras en línea, si se seleccionan 10 clientes al azar, determina el porcentaje de que al menos seis prefieran comprar en línea:
buenos dias me puede decir que tipo de problema de probabilidad es el siguiente: en un grupo de matematicas el 80.5% de los alumnos acreditan la materia. si se toma una muestra de 100 alumnos calcular la probabilidad de que: a) mas del 88% acrediten la materia b) entre el 85 y el 90% acrediten la materia c)mas del 72% acrediten la materia d) menos del 80.5 acrediten la materia e) entre 71 y el 76% acrediten la materia f) menos del 75% acrediten la materia g) entre el 78 y el 84 % acrediten la materia h) menos del 90% acrediten la materia. Me puede orientar por favor
Dos jóvenes hacen una apuesta, el primero apuesta al segundo que en 5 intentos de valado al ambos obtienen 2 soles.
A) ¿Quien tiene la mayor probabilidad de ganar?
(p)=0,7
¿Y si te preguntan la probabilidad de que ocurra algo?
Necesito la demostración de que la varianza de una distribucion binomial es n.p.q
Distribución Binomial. (n! (x! (n-x)!)) (px)(q^(n-x))
La probabilidad de que un hombre acierte en el bianco es de. Si dispara 10 veces.
a) ¿Cuál es la probabilidad de que acierte exactamente en tres ocasiones?
b) ¿Cuál es la probabilidad de que acierte siete o más ocasiones?
c) ¿Cuál es la probabilidad de que acerté por lo menos 8 ocasiones?