Capítulos

Los/las mejores profesores/as de Matemáticas que están disponibles
Multiplicación de complejos en forma polar
La multiplicación de dos números complejos es otro número complejo tal que:
1 Su módulo es el producto de los módulos.
2 Su argumento es la suma de los argumentos.

Ejemplo:
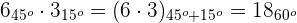
Producto por un complejo de módulo 1
Al multiplicar un número complejo  por
por 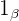 se gira
se gira 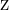 un ángulo
un ángulo  alrededor del origen.
alrededor del origen.


División de complejos en forma polar
La división de dos números complejos es otro número complejo tal que:
1Su módulo es el cociente de los módulos.
2Su argumento es la diferencia de los argumentos.
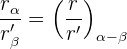
Ejemplo:
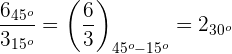
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Muchas gracias por las paginas fantásticas que publicáis y nos ayudan tanto .
En el número 2 e de este apartado ¿puede ser que el eje de abscisas los valores necesiten un 3 multiplicando al 1/2? porque así el módulo sería 3
Muchas gracias de antemano
Hola te felicitamos por tu buena observación, vamos a trabajar para rectificar ese error.
Me interesa poder descargar esos materiales sobre números complejos que aparecen en este sitio
Hola, lo sentimos pero esa función(descargar) no la tenemos en funcionamiento, pero puedes ver el material en la pagina las veces que desees.
El resultado para el seno de un angulo tripe que ustesdes muestran es incorrecto, quiza error de transcripcion al momento de escribir. El resultado correcto es: sen(3a) = 3cos^2(a).sen(a) – sen^3(a). O su forma equivalente: sen(3a) = 3sen(a) – 4sen^3(a)
Hola te agradecemos tus observaciones, una disculpa ya se corrigió.
Me podrías ayudar con (Interpretación de un número complejo)
3. Calcular las siguientes operaciones
a) ((3 + i)(3 – 2i) – (2i – 3) ^ 2)/(2i ^ 20 – i ^ 13)
b) (1 – (2 + 3i) ^ 2 * (1 – 2i))/(2i ^ 77 – i ^ 726)
c) (2 – 3i) ^ 3
Me pueden ayudar con este ejercicio por favor