Calcula  para que el número complejo que obtenemos de la siguiente división esté representado en la bisectriz del primer cuadrante
para que el número complejo que obtenemos de la siguiente división esté representado en la bisectriz del primer cuadrante
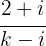
1 Para que el afijo  , del complejo esté en la bisectriz del primer cuadrante tiene que cumplirse:
, del complejo esté en la bisectriz del primer cuadrante tiene que cumplirse:  . Multiplicamos numerador y denominador por el conjugado del denominador para realizar el cociente
. Multiplicamos numerador y denominador por el conjugado del denominador para realizar el cociente
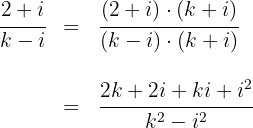
2 Escribimos la componente real e imaginaria recordando que 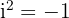
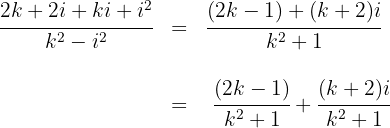
3 Igualamos ambas componentes, como ambas tienen el mismo denominador, entonces los numeradores también son iguales
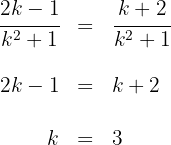
Así el valor buscado es 
Halla el valor de  para que el cociente sea: un número imaginario puro; un número real
para que el cociente sea: un número imaginario puro; un número real

1 Multiplicamos numerador y denominador por el conjugado del denominador para realizar el cociente

2 Escribimos la componente real e imaginaria recordando que 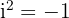
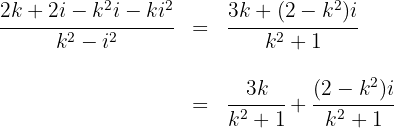
3 Para obtener un número imaginario puro se requiere que la parte real sea cero
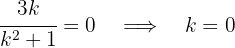
Así para que el número sea imaginario puro se requiere 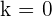
4 Para obtener un número real se requiere que la parte imaginaria sea cero

Así para que el número sea real se requiere 
Se considera el complejo 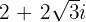 , se gira
, se gira  alrededor del origen de coordenadas en sentido contrario a las agujas del reloj. Hallar el complejo obtenido después del giro.
alrededor del origen de coordenadas en sentido contrario a las agujas del reloj. Hallar el complejo obtenido después del giro.
1 Escribimos el número en forma polar
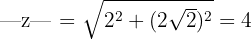
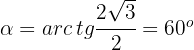
entonces 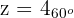
2 Multiplicamos por un complejo de módulo 1 y argumento 
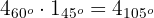
El número buscado es 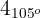
Hallar las coordenadas de los vértices de un hexágono regular de centro el origen de coordenadas, sabiendo que uno de los vértices es el afijo del complejo 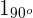
1 Los vértices son los afijos de las raíces sextas de otro complejo 

2 Calculamos las raíces sextas

3 Calculamos los valores para 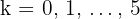
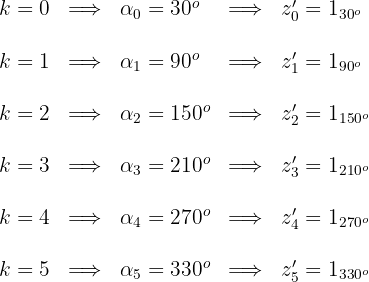
4 Las coordenadas buscadas son
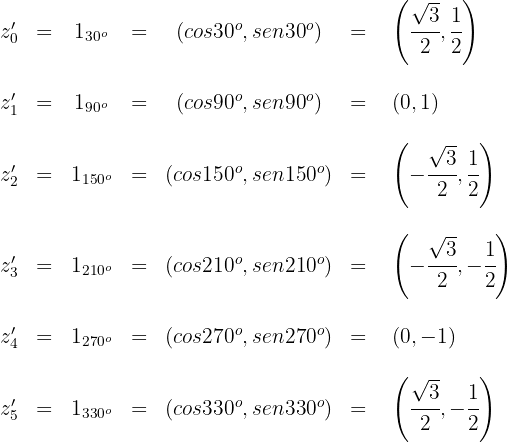
Determina el valor de  y
y  para que el cociente
para que el cociente 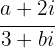 sea igual a
sea igual a 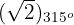
1 Expresamos 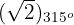 como número complejo
como número complejo

2 Igualamos el cociente con la expresión anterior, multiplicamos ambos lados por  y resolvemos
y resolvemos
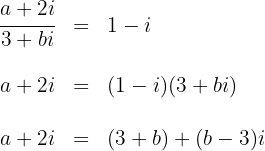
3 Igualamos la parte imaginaria de ambos lados y obtenemos

4 Igualamos la parte real de ambos lados y obtenemos

¿Cuáles son las coordenadas del punto que se obtiene al girar  , en sentido antihorario alrededor del origen, el afijo del complejo
, en sentido antihorario alrededor del origen, el afijo del complejo 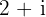 ?
?
1 Sabemos que

2 Multiplicamos por el complejo de módulo 1 y argumento 
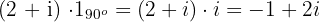
Las coordenadas buscadas son 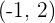
 .
.1 Escribimos  en forma polar
en forma polar
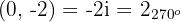
2 Los vértices son los afijos de las raíces cuartas de otro complejo 
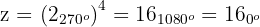
3 Calculamos las raíces cuartas
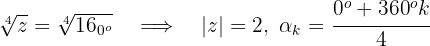
4 Calculamos los valores para 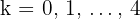
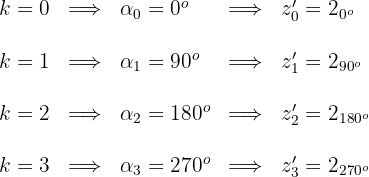
5 Las coordenadas buscadas son
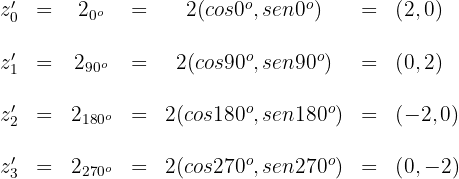
1 Escribimos el número complejo  en forma polar
en forma polar
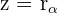
2 Escribimos su conjugado  en forma polar
en forma polar
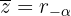
3 La suma de las componentes reales es seis, de lo que se obtiene
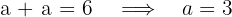
4 La suma de sus módulos es 10, de lo que se obtiene

5 De la expresión del módulo  se obtiene
se obtiene

5 Calculamos el argumento
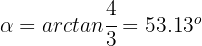
Así, los números complejos son
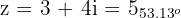

Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Muchas gracias por las paginas fantásticas que publicáis y nos ayudan tanto .
En el número 2 e de este apartado ¿puede ser que el eje de abscisas los valores necesiten un 3 multiplicando al 1/2? porque así el módulo sería 3
Muchas gracias de antemano
Hola te felicitamos por tu buena observación, vamos a trabajar para rectificar ese error.
Me interesa poder descargar esos materiales sobre números complejos que aparecen en este sitio
Hola, lo sentimos pero esa función(descargar) no la tenemos en funcionamiento, pero puedes ver el material en la pagina las veces que desees.
El resultado para el seno de un angulo tripe que ustesdes muestran es incorrecto, quiza error de transcripcion al momento de escribir. El resultado correcto es: sen(3a) = 3cos^2(a).sen(a) – sen^3(a). O su forma equivalente: sen(3a) = 3sen(a) – 4sen^3(a)
Hola te agradecemos tus observaciones, una disculpa ya se corrigió.
Me podrías ayudar con (Interpretación de un número complejo)
3. Calcular las siguientes operaciones
a) ((3 + i)(3 – 2i) – (2i – 3) ^ 2)/(2i ^ 20 – i ^ 13)
b) (1 – (2 + 3i) ^ 2 * (1 – 2i))/(2i ^ 77 – i ^ 726)
c) (2 – 3i) ^ 3
Me pueden ayudar con este ejercicio por favor