En ocasiones, cuando realizamos una prueba de hipótesis, nuestra hipótesis nula pueden ser de la forma
para la media, o
si se trata de una proporción.
En este caso, la hipótesis alternativa es del tipo
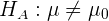
cuando se trata de la media, o
para la proporción.
Procedimiento y fórmulas del contraste bilateral
A partir de aquí consideramos sólo la prueba de hipótesis para la media. El procedimiento es muy similar para las proporciones y se indicará cuando sea diferente.
Observemos que la hipótesis nula es una igualdad. Por lo tanto, rechazaremos la hipótesis nula cuando la media muestral sea mucho mayor o mucho menor a la hipotética.
En otras palabras, la región de rechazo se divide en dos regiones alejadas de la media. Estas regiones (o colas) de la región de rechazo son simétricas respecto a la media hipotética. Además, la probabilidad 
de estas regiones se conoce como el nivel de significación.
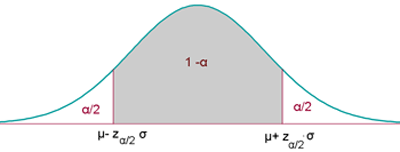
Por tanto, en este caso la región de aceptación es el intervalo de probabilidad 
para 
. Este intervalo se obtiene al descargar las colas de la región de rechazo y está dado por
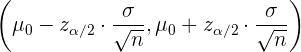
en el caso de la prueba de hipótesis para la media hipotética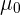 
.
Por otro lado, si hacemos una prueba de hipótesis para la proporción 
, entonces la región de aceptación está dada por
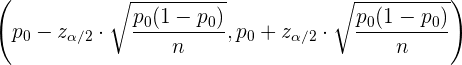
En estas regiones, 
es el tamaño de muestra,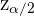 
es el valor crítico, 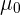es la media hipotética y 
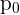es la proporción hipotética.
Los valores críticos 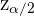para la significancia se resumen en la siguiente tabla:
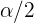|  |  | Intervalos característicos |
|---|---|---|---|
| 0.90 | 0.05 | 1.645 |  |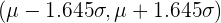
| 0.95 | 0.025 | 1.96 |  |
| 0.99 | 0.005 | 2.575 |  |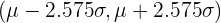
Observemos que esta prueba de conoce como bilateral ya que la hipótesis se rechaza si la media (o proporción) muestral es mucho mayor o menor que la hipotética, es decir, la hipótesis se puede rechazar en ambos lados de 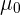(o ).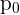
Ejemplo resuelto del contraste bilateral
1 Se sabe que la desviación típica de las notas de cierto examen de Matemáticas es 2,4. Para una muestra de 36 estudiantes se obtuvo una nota media de 5,6. ¿Sirven estos datos para confirmar la hipótesis de que la nota media del examen fue de 6, con un nivel de confianza del 95%?
Realizamos los pasos para hacer una prueba de hipótesis:
a Primero enunciamos las hipótesis nula y alternativa. La hipótesis nula es
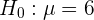
es decir, que la nota promedio es 6. Por otro lado, la hipótesis alternativa es
que significa que la nota promedio es diferente a 6. Observemos que como la hipótesis nula es una igualdad, entonces haremos un constraste bilateral.
b Luego construimos la zona de aceptación. Como tenemos que el nivel de confianza es 95%, entonces el nivel de significancia es 
. A este valor de significancia le corresponde el valor crítico
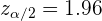
De este modo, el intervalo de aceptación para la media es
es decir,
c Después realizamos la verificación: la media obtenida en la muestra es de 5.6.
d Por tanto, decidimos que la hipótesis nula 
se acepta debido a que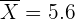 
se encuentra dentro del intervalo de aceptación. Es decir, concluimos que no hay evidencia suficiente para decir que la media es diferente a 6.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El servicio de emergencia para ciertas áreas rurales de Ohio con frecuencia es un problema, especialmente durante los meses de invierno. El jefe del Departamento de Bomberos de Danville, Township está preocupado por el tiempo de respuesta a las llamadas de emergencia. Ordena una investigación para determinar si la distancia del lugar de la llamada, medida en millas, puede explicar el tiempo de respuesta, medido en minutos.Con base en 37 emergencias, se recolectaron los siguientes datos: ∑X = 234 EY = 831 ∑XY = 5,890
2X*=1.796 2r² =20,037
a. ¿Cuál es el tiempo de respuesta a una llamada que proviene de ocho millas de la estación de bomberos?. ¿Qué tan dependiente es dicha estimación, con base en el grado de dispersión de los puntos de datos alrededor de la recta de regresión?
De una población de 2,500 estudiantes de la universidad Unibe 60% Ingeniería industrial, con un nivel de confianza de 95% y un margen de error de 5%, determine la muestra?
Nota: cuando no conocemos el valor de p y q se les asigna 50% a cada uno y las cantidades que aparecen en porcentaje debe dividirse en 100.
La alcaldía de la ciudad está preocupada por el retiro masivo de las industrias hacía la capital del país, por lo usted como un importante analista en términos económicos lo debe asesorar, se seleccionó una muestra de 500 empresas de las cuales la 300 aún permanecen en la ciudad, la proporción de empresas que han salido de la ciudad se encuentra entre:
Pregunta 5Seleccione una:
a.
40 y 60%
b.
46 y 56%
c.
36 y 44 %
d.
30 y 40 %
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra