La inferencia estadística es el conjunto de métodos y técnicas que permiten inducir, a partir de la información empírica proporcionada por una muestra, cuál es el comportamiento de una determinada población con un riesgo de error medible en términos de probabilidad. Es decir, estudia los métodos para sacar conclusiones generales de toda una población a partir del análisis de una muestra.
Algunos ejemplos donde encontramos el uso de la estadística inferencial es en
- Sondeos de tendencia de voto
- Análisis de mercado
- Epidemiología médica
- Climatología

Muestreo
En cierta cadena de centros comerciales trabajan 150 personas en el departamento de personal, 450 en el departamento de ventas, 200 en el departamento de contabilidad y 100 en el departamento de atención al cliente. Con objeto de realizar una encuesta laboral, se quiere seleccionar una muestra de 180 trabajadores.
¿Qué tipo de muestreo deberíamos utilizar para la selección de la muestra si queremos que incluya a trabajadores de los cuatro departamentos mencionados?
¿Qué número de trabajadores tendríamos que seleccionar en cada departamento atendiendo a un criterio de proporcionalidad?
1¿Qué tipo de muestreo deberíamos utilizar para la selección de la muestra si queremos que incluya a trabajadores de los cuatro departamentos mencionados?
Utilizaremos un muestreo aleatorio estratificado, ya que queremos que haya representantes de cada uno de los departamentos, tomaremos una muestra significativa que represente la proporción de empleados que hay en cada departamento.
2¿Qué número de trabajadores tendríamos que seleccionar en cada departamento atendiendo a un criterio de proporcionalidad?
Para poder elegir una cantidad proporcional de cada departamento, primero debemos conocer la proporción que tendrá el tamaño de la muestra respecto a la totalidad de trabajadores, esto es:
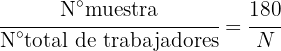
donde
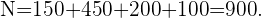
Ahora, la cantidad de trabajadores a seleccionar de cada departamento, debe conservar la proporción que hemos calculado, es decir, el número  de trabajadores en cada departamento debe cumplir:
de trabajadores en cada departamento debe cumplir:
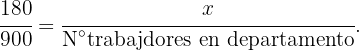
Entonces tenemos
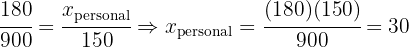

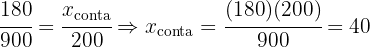
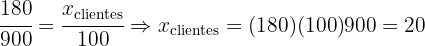
Y además podemos corroborar que
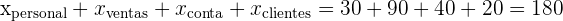
que es justamente el tamaño de la muestra.
En cierto barrio se quiere hacer un estudio para conocer mejor el tipo de actividades de ocio que gustan más a sus habitantes. Para ello van a ser encuestados 100 individuos elegidos al azar.
Explicar qué procedimiento de selección sería más adecuado utilizar: muestreo con o sin reposición. ¿Por qué?
Como los gustos cambian con la edad y se sabe que en el barrio viven 2,500 niños, 7,000 adultos y 500 ancianos, posteriormente se decide elegir la muestra anterior utilizando un muestreo estratificado con asignación proporcional. Determinar el tamaño muestral correspondiente a cada estrato.
1 Explicar qué procedimiento de selección sería más adecuado utilizar: muestreo con o sin reposición. ¿Por qué?
Como la población es finita, entonces hacer muestreo con reemplazo nos permitirá utilizar las fórmulas que hemos estudiado.
Sin embargo, es posible hacer muestreo sin reemplazo, con el único inconveniente que los cálculos serán un poco más complicados.
2 Como los gustos cambian con la edad y se sabe que en el barrio viven 2,500 niños, 7,000 adultos y 500 ancianos, posteriormente se decide elegir la muestra anterior utilizando un muestreo estratificado con asignación proporcional. Determinar el tamaño muestral correspondiente a cada estrato.
Sea  el tamaño de la población y
el tamaño de la población y 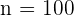 el tamaño de la muestra. Denotaremos como
el tamaño de la muestra. Denotaremos como 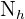 al tamaño del estrato
al tamaño del estrato  y
y  al tamaño de muestra que tomamos de
al tamaño de muestra que tomamos de  . En el muestreo estratificado con asignación proporcional se cumple que
. En el muestreo estratificado con asignación proporcional se cumple que
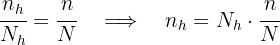
Por lo que debemos encontrar los valores  para cada estrato. Notemos que los tamaños de cada estrato
para cada estrato. Notemos que los tamaños de cada estrato  (niños),
(niños), 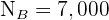 (adultos) y
(adultos) y 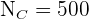 (ancianos).
(ancianos).
Así, el tamaño de muestra de niños es:
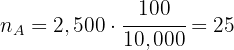
El tamaño de muestra de adultos es:
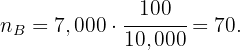
Por último, el tamaño de muestra de ancianos es:
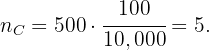
Observamos que los tamaños de muestra suman 100:
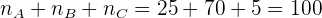
Una empresa de fabricación de componentes electrónicos cuenta con tres plantas en las cuales se producen 10 000, 8000 y 5000 componentes del mismo tipo, respectivamente. Se requiere obtener una muestra de 1150 componentes para un estudio de durabilidad. Si se realiza un muestreo estratificado con asignación proporcional por planta, ¿qué cantidad de elementos se consideran?
Para poder elegir una cantidad proporcional de cada planta, primero debemos conocer la proporción que tendrá el tamaño de la muestra respecto a la totalidad de componentes, esto es:
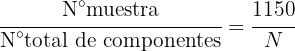
donde
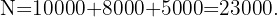
Ahora, la cantidad de componentes a seleccionar de cada planta, debe conservar la proporción que hemos calculado, es decir, el número  de componentes en cada planta debe cumplir:
de componentes en cada planta debe cumplir:
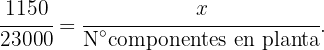
Entonces tenemos
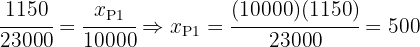
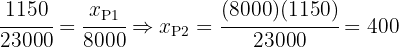
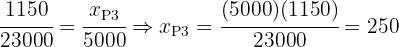
Y además podemos corroborar que
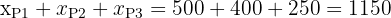
que es justamente el tamaño de la muestra.
Una empresa decide encuestar a sus clientes, para ello sabe que dispone de 500 clientes en España y 450 en Francia. Se requiere obtener una muestra de 100 clientes utilizando muestreo estratificado con asignación proporcional por cada país, ¿qué cantidad de elementos se consideran?
Para poder elegir una cantidad proporcional de cada país, primero debemos conocer la proporción que tendrá el tamaño de la muestra respecto a la totalidad de clientes, esto es:
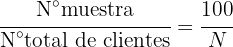
donde
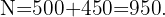
Ahora, la cantidad de clientes a seleccionar de cada país, debe conservar la proporción que hemos calculado, es decir, el número  de clientes en cada país debe cumplir:
de clientes en cada país debe cumplir:
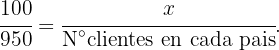
Entonces tenemos
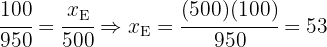
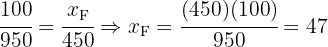
Y además podemos corroborar que
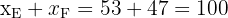
que es justamente el tamaño de la muestra.
Se aplica un nuevo fertilizante a tres tipos distintos de plantas, 350 del tipo 1, 250 del tipo 2 y 200 del tipo 3. Se requiere obtener una muestra de 80 plantas utilizando muestreo estratificado con asignación proporcional por cada tipo, ¿qué cantidad de elementos se consideran?
Para poder elegir una cantidad proporcional de cada tipo de planta, primero debemos conocer la proporción que tendrá el tamaño de la muestra respecto a la totalidad de plantas, esto es:
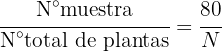
donde
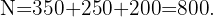
Ahora, la cantidad de plants a seleccionar de cada tipo, debe conservar la proporción que hemos calculado, es decir, el número  de plantas de cada tipo debe cumplir:
de plantas de cada tipo debe cumplir:
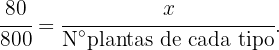
Entonces tenemos
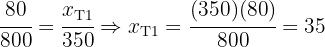
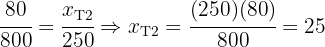
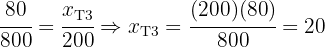
Y además podemos corroborar que
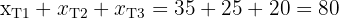
que es justamente el tamaño de la muestra.
Nivel de confianza
La cantidad de hemoglobina en sangre del hombre sigue una ley normal con una desviación típica de 2g/dl. Calcule el nivel de confianza de una muestra de 12 extracciones de sangre que indique que la media poblacional de hemoglobina en sangre está entre 13 y 15 g/dl.
Necesitamos encontrar el nivel de confianza para que la media del nivel de hemoglobina en sangre esté entre 13 y 15 g/dl. Para establecer esto necesitamos conocer el nivel de significancia y esto lo podemos saber a través de la fórmula del error estándar, este es
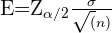
donde  es la desviación típica,
es la desviación típica,  es el tamaño de la muestra y
es el tamaño de la muestra y  es el valor Z de una distribución Normal estándar tal que
es el valor Z de una distribución Normal estándar tal que

Como queremos conocer la confiabilidad de que la media esté entre 13 y 15 g/dl, tomemos este intervalo como estimador para el error estándar, sustituyendo los valores en la fórmula tenemos
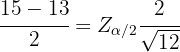
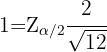
despejando
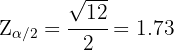
Conociendo ya el valor de  podemos calcular la probabilidad correspondiente. Esto se solía hacer mediante tablas, hoy en día tenemos herramientas más sencillas de utilizar, como lo es Wolfram. Entonces tenemos que la probabilidad es
podemos calcular la probabilidad correspondiente. Esto se solía hacer mediante tablas, hoy en día tenemos herramientas más sencillas de utilizar, como lo es Wolfram. Entonces tenemos que la probabilidad es
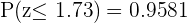
Dado que hemos calculado  , es necesario restar la probabilidad del extremo izquierdo de la distribución normal, para esto consideremos
, es necesario restar la probabilidad del extremo izquierdo de la distribución normal, para esto consideremos
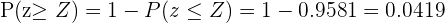
entonces
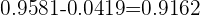
Por lo tanto, el nivel de confianza de que la media de hemoglobina en sangre se encuentre entre 15 y 13 g/dl es del 91.62% para una muestra de 12 extracciones de sangre.
Las ventas mensuales de una tienda de electrodomésticos siguen una distribución normal, con desviación típica 900 €. En un estudio estadístico de las ventas realizadas en los últimos nueve meses, se ha encontrado un intervalo de confianza para la media mensual de las ventas, cuyos extremos son 4 663 € y 5 839 €. ¿Cuál ha sido la media de las ventas en estos nueve meses? ¿Cuál es el nivel de confianza para este intervalo?
1 ¿Cuál ha sido la media de las ventas en estos nueve meses?
Cuando calculamos el intervalo de confianza de la media de una distribución normal, la media siempre se encontrará a la mitad del intervalo. Por lo tanto, la media es
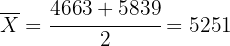
Esto es, la media fue de 5 251 €.
2 ¿Cuál es el nivel de confianza para este intervalo?
Tenemos que  ,
,  y
y 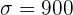 . De aquí se sigue que el límite inferior se calculó utilizando
. De aquí se sigue que el límite inferior se calculó utilizando
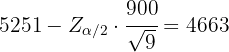
Es decir,
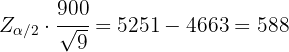
Por lo que
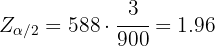
De aquí se sigue que 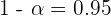 , por lo que el nivel de confianza fue de 95%.
, por lo que el nivel de confianza fue de 95%.
El tiempo que tardan las cajeras de un supermercado en cobrar a los clientes sigue una distribución normal con media desconocida y desviación típica 0,5 minutos. Para una muestra aleatoria de 25 clientes se obtuvo un tiempo medio de 5,2 minutos. Calcula el intervalo de confianza al nivel del 95% para el tiempo medio que se tarda en cobrar a los clientes e indica el tamaño muestral necesario para estimar dicho tiempo medio con un el error de 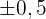 minutos y un nivel de confianza del 95%.
minutos y un nivel de confianza del 95%.
1 Calcula el intervalo de confianza al nivel del 95% para el tiempo medio que se tarda en cobrar a los clientes.
Como la muestra consiste de 25 clientes, entonces para calcular el intervalo de confianza, utilizamos la fórmula:
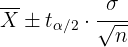
donde 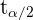 es el valor crítico tal que
es el valor crítico tal que  donde
donde  es una variable aleatoria que sigue una distribución t-Student con 24 grados de libertad.
es una variable aleatoria que sigue una distribución t-Student con 24 grados de libertad.
El valor de 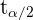 lo podemos obtener de una tabla de distribución t, o utilizando un software. El resultado es
lo podemos obtener de una tabla de distribución t, o utilizando un software. El resultado es 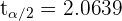
Así, el intervalo de confianza es

2 Indica el tamaño muestral necesario para estimar dicho tiempo medio con un el error de 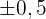 minutos y un nivel de confianza del 95%.
minutos y un nivel de confianza del 95%.
Para encontrar el tamaño muestral reemplazaremos 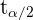 por
por  , el cual proviene de una distribución normal estándar. Como el error debe ser
, el cual proviene de una distribución normal estándar. Como el error debe ser  , entonces se debe tener
, entonces se debe tener
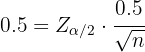
donde 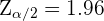 . Así, al despejar
. Así, al despejar  tenemos
tenemos
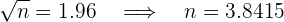
es decir, el tamaño de muestra debe ser al menos de  .
.
Las alturas de una muestra de 16 plantas siguen una distribución normal, con desviación típica 9 cm. Se ha encontrado un intervalo de confianza para la media de las alturas, cuyos extremos son 23 y 35 cm. ¿Cuál es el nivel de confianza para este intervalo?
Cuando calculamos el intervalo de confianza de la media de una distribución normal, la media siempre se encontrará a la mitad del intervalo. Por lo tanto, la media es
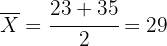
Esto es, la media fue de 29 cm.
¿Calculamos el nivel de confianza para este intervalo
Tenemos que 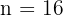 ,
, 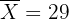 y
y 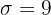 . De aquí se sigue que el límite inferior se calculó utilizando
. De aquí se sigue que el límite inferior se calculó utilizando
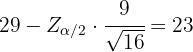
Es decir,
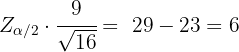
Por lo que
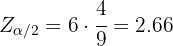
De aquí se sigue que 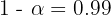 , por lo que el nivel de confianza fue de 99%.
, por lo que el nivel de confianza fue de 99%.
La duración de un nuevo alimento libre de conservadores tiene un intervalo de confianza de 5 a 10 días para una muestra de tamaño 25 que sigue una distribución normal, con desviación típica 8 días. ¿Cuál es el nivel de confianza para este intervalo?
Cuando calculamos el intervalo de confianza de la media de una distribución normal, la media siempre se encontrará a la mitad del intervalo. Por lo tanto, la media es
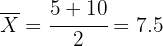
Esto es, la media fue de 7.5 días.
¿Calculamos el nivel de confianza para este intervalo
Tenemos que 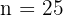 ,
, 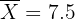 y
y 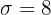 . De aquí se sigue que el límite inferior se calculó utilizando
. De aquí se sigue que el límite inferior se calculó utilizando
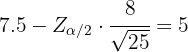
Es decir,
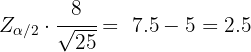
Por lo que
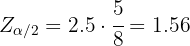
De aquí se sigue que 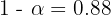 , por lo que el nivel de confianza fue de 88%.
, por lo que el nivel de confianza fue de 88%.
Prueba de hipótesis a dos colas
Un fabricante de lámparas eléctricas está ensayando un nuevo método de producción que se considerará aceptable si las lámparas obtenidas por este método dan lugar a una población normal de duración media 2400 horas, con una desviación típica igual a 300. Se toma una muestra de 100 lámparas producidas por este método y esta muestra tiene una duración media de 2320 horas. ¿Se puede aceptar la hipótesis de validez del nuevo proceso de fabricación con un riesgo igual o menor al 5%?
Este es un ejercicio donde tenemos que hacer una prueba de hipótesis, el objetivo es saber si la muestra tomada es evidencia suficiente para afirmar que el nuevo método de producción dará lugar a lámparas con una duración media de 2400 horas y desviación típica de 300 horas con un 5% de probabilidad (o menos) a equivocarse.
El primer paso es establecer la hipótesis nula ( ) y la hipótesis alternativa (
) y la hipótesis alternativa ( ), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
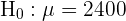
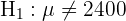
Para realizar la prueba de hipótesis necesitaremos calcular nuestro estadístico; dado que estamos suponiendo que el tiempo de duración se distribuye de acuerdo a una distribución normal y el tamaño de muestra es igual a 100, usaremos el estadístico Z (variable aleatoria de una Normal estándar), este es
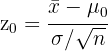
donde  es la media de la muestra,
es la media de la muestra, 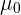 es la media de
es la media de  ,
,  es la desviación típica y
es la desviación típica y  es el tamaño de la muestra. Sustituyendo los valores tenemos
es el tamaño de la muestra. Sustituyendo los valores tenemos
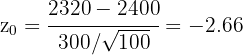
Ahora, calculemos el p-valor para  , dado que la hipótesis alternativa es una negación (
, dado que la hipótesis alternativa es una negación ( ) este es un análisis de dos colas, para este caso el p-valor se calcula como
) este es un análisis de dos colas, para este caso el p-valor se calcula como
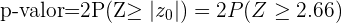
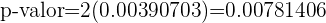
La probabilidad de error es del 5%, lo que quiere decir que el nivel de significancia que se está considerando es del 0.05 y tenemos que p-valor=0.0078; la hipótesis nula se rechaza si p-valor es menor al valor de significancia, que es justamente lo que tenemos
 0.0078 < 0.05[/latex]
0.0078 < 0.05[/latex]
Por lo tanto, hay evidencia suficiente para rechazar la hipótesis de que el nuevo método de producción dará lugar a lámparas con una duración media de 2400 horas y desviación típica de 300 con un 5% de probabilidad de equivocarnos.
El control de calidad una fábrica de pilas y baterías sospecha que hubo defectos en la producción de un modelo de batería para teléfonos móviles, bajando su tiempo de duración. Hasta ahora el tiempo de duración en conversación seguía una distribución normal con media 300 minutos y desviación típica 30 minutos. Sin embargo, en la inspección del último lote producido, antes de enviarlo al mercado, se obtuvo que de una muestra de 60 baterías el tiempo medio de duración en conversación fue de 290 minutos. Suponiendo que ese tiempo sigue siendo Normal con la misma desviación típica: ¿Se puede concluir que las sospechas del control de calidad son ciertas a un nivel de significación del 1%?
Este es un ejercicio donde tenemos que hacer una prueba de hipótesis, el objetivo es saber si la muestra tomada es evidencia suficiente para afirmar, con el 1% de probabilidad a equivocarnos, que la sospecha del equipo de control de calidad es cierta, en referencia a la disminución de la calidad de las baterias.
El primer paso es establecer la hipótesis nula ( ) y la hipótesis alternativa (
) y la hipótesis alternativa ( ), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
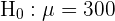
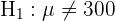
Para realizar la prueba de hipótesis necesitaremos calcular nuestro estadístico; dado que estamos suponiendo que el tiempo de duración se distribuye de acuerdo a una distribución normal y el tamaño de muestra es igual a 60, usaremos el estadístico Z (variable aleatoria de una Normal estándar), este es
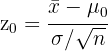
donde  es la media de la muestra,
es la media de la muestra, 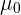 es la media de
es la media de  ,
,  es la desviación típica y
es la desviación típica y  es el tamaño de la muestra. Sustituyendo los valores tenemos
es el tamaño de la muestra. Sustituyendo los valores tenemos
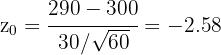
Ahora, calculemos el p-valor para 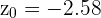 , dado que la hipótesis alternativa es una negación (
, dado que la hipótesis alternativa es una negación ( ) este es un análisis de dos colas, para este caso el p-valor se calcula como
) este es un análisis de dos colas, para este caso el p-valor se calcula como
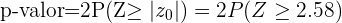

La probabilidad de error es del 1%, lo que quiere decir que el nivel de significancia que se está considerando es del 0.01 y tenemos que p-valor=0.0098; la hipótesis nula se rechaza si p-valor es menor al valor de significancia, que es justamente lo que tenemos
 0.0098 < 0.01[/latex]
0.0098 < 0.01[/latex]
Por lo tanto, hay evidencia suficiente para rechazar la hipótesis de que la duración media de la batería es de 300 minutos con desviación típica de 30 minutos con un 1% de probabilidad a equivocarse con una muestra de tamaño 60, es decir, podemos concluir que las sospechas del equipo de control de calidad sí son ciertas.
Se cree que el nivel medio de protombina en una población normal es de 20 mg/100 ml de plasma con una desviación típica de 4 miligramos/100 ml. Para comprobarlo, se toma una muestra de 40 individuos en los que la media es de 18.5 mg/100 ml. ¿Se puede aceptar la hipótesis, con un nivel de significación del 5%?
Este es un ejercicio donde tenemos que hacer una prueba de hipótesis, el objetivo es saber si la muestra tomada es evidencia suficiente para afirmar, con el 5% de probabilidad a equivocarnos, que el nivel medio de protombina es de 20 mg/100 ml de plasma con una desviación típica de 4 mg/100 ml. El primer paso es establecer la hipótesis nula ( ) y la hipótesis alternativa (
) y la hipótesis alternativa ( ), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
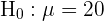
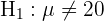
Para realizar la prueba de hipótesis necesitaremos calcular nuestro estadístico; dado que estamos suponiendo que la concentración de protombina se distribuye de acuerdo a una distribución normal y el tamaño de muestra es igual a 40, usaremos el estadístico Z (variable aleatoria de una Normal estándar), este es
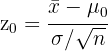
donde  es la media de la muestra,
es la media de la muestra, 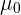 es la media de
es la media de  ,
,  es la desviación típica y
es la desviación típica y  es el tamaño de la muestra. Sustituyendo los valores tenemos
es el tamaño de la muestra. Sustituyendo los valores tenemos
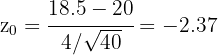
Ahora, calculemos el p-valor para  , dado que la hipótesis alternativa es una negación (
, dado que la hipótesis alternativa es una negación ( ) este es un análisis de dos colas, para este caso el p-valor se calcula como
) este es un análisis de dos colas, para este caso el p-valor se calcula como
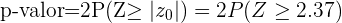
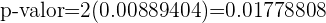
La probabilidad de error es del 5%, lo que quiere decir que el nivel de significancia que se está considerando es del 0.05 y tenemos que p-valor=0.0177; la hipótesis nula se rechaza si p-valor es menor al valor de significancia, que es justamente lo que tenemos
 0.0177 < 0.05[/latex]
0.0177 < 0.05[/latex]
Por lo tanto, hay evidencia suficiente para rechazar la hipótesis de que el el nivel medio de protombina es de 20 mg/100 ml de plasma con una desviación típica de 4 mg/100 ml, con un nivel de significancia del 5% con una muestra de tamaño 40.
Un inspector sospecha que el nivel medio de azúcar en un refresco embotellado es de 40 g/350 ml de contenido. Analiza 30 refrescos en los que la media es 41 g/350 ml de azúcar con una desviación típica de 4 g/350 ml. ¿Se puede aceptar la hipótesis, con un nivel de significación del 5%?
Este es un ejercicio donde tenemos que hacer una prueba de hipótesis, el objetivo es saber si la muestra tomada es evidencia suficiente para afirmar, con el 5% de probabilidad a equivocarnos, que el nivel medio de azúcar es de 40 g/350 ml de refresco con una desviación típica de 4 g/350 ml. El primer paso es establecer la hipótesis nula ( ) y la hipótesis alternativa (
) y la hipótesis alternativa ( ), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
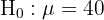
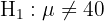
Para realizar la prueba de hipótesis necesitaremos calcular nuestro estadístico; dado que estamos suponiendo que la concentración de azúcar se distribuye de acuerdo a una distribución normal y el tamaño de muestra es igual a 30, usaremos el estadístico Z (variable aleatoria de una Normal estándar), este es
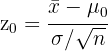
donde  es la media de la muestra,
es la media de la muestra, 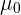 es la media de
es la media de  ,
,  es la desviación típica y
es la desviación típica y  es el tamaño de la muestra. Sustituyendo los valores tenemos
es el tamaño de la muestra. Sustituyendo los valores tenemos
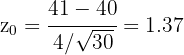
Ahora, calculemos el p-valor para 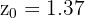 , dado que la hipótesis alternativa es una negación (
, dado que la hipótesis alternativa es una negación ( ) este es un análisis de dos colas, para este caso el p-valor se calcula como
) este es un análisis de dos colas, para este caso el p-valor se calcula como
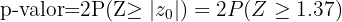
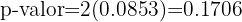
La probabilidad de error es del 5%, lo que quiere decir que el nivel de significancia que se está considerando es del 0.05 y tenemos que p-valor=0.1706; la hipótesis nula se rechaza si p-valor es menor al valor de significancia, pero nosotros tenemos
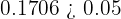
Por lo tanto, hay evidencia suficiente para aceptar la hipótesis de que el el nivel medio de azúcar es de 40 g/350 ml de contenido con una desviación típica de 4 g/350 ml, con un nivel de significancia del 5% con una muestra de tamaño 30.
Una empresa afirma que en promedio su producto tiene un peso de 45 g. Un inspector sospecha que la cantidad de producto es diferente al que dice la empresa, para lo cual toma una muestra de 50 elementos de donde obtiene una media de 43 g con una desviación típica de 4 g. ¿Se puede aceptar la hipótesis, con un nivel de significación del 5%?
Este es un ejercicio donde tenemos que hacer una prueba de hipótesis, el objetivo es saber si la muestra tomada es evidencia suficiente para afirmar, con el 5% de probabilidad a equivocarnos, que el nivel medio de producto es de 45 g con una desviación típica de 4 g. El primer paso es establecer la hipótesis nula ( ) y la hipótesis alternativa (
) y la hipótesis alternativa ( ), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
), donde generalmente el resultado nos lleva a rechazar o no rechazar la hipótesis nula.
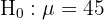
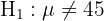
Para realizar la prueba de hipótesis necesitaremos calcular nuestro estadístico; dado que estamos suponiendo que la concentración de azúcar se distribuye de acuerdo a una distribución normal y el tamaño de muestra es igual a 50, usaremos el estadístico Z (variable aleatoria de una Normal estándar), este es
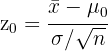
donde  es la media de la muestra,
es la media de la muestra, 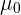 es la media de
es la media de  ,
,  es la desviación típica y
es la desviación típica y  es el tamaño de la muestra. Sustituyendo los valores tenemos
es el tamaño de la muestra. Sustituyendo los valores tenemos
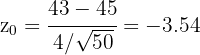
Ahora, calculemos el p-valor para 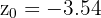 , dado que la hipótesis alternativa es una negación (
, dado que la hipótesis alternativa es una negación ( ) este es un análisis de dos colas, para este caso el p-valor se calcula como
) este es un análisis de dos colas, para este caso el p-valor se calcula como
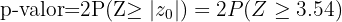
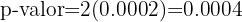
La probabilidad de error es del 5%, lo que quiere decir que el nivel de significancia que se está considerando es del 0.05 y tenemos que p-valor=0.0004; la hipótesis nula se rechaza si p-valor es menor al valor de significancia, pero nosotros tenemos
 0.0004 < 0.05[/latex]
0.0004 < 0.05[/latex]
Por lo tanto, hay evidencia suficiente para rechazar la hipótesis de que el el nivel medio de producto es de 45 g con una desviación típica de 4 g, con un nivel de significancia del 5% con una muestra de tamaño 50.
Si necesitas apoyo adicional con los conceptos de estadística, no dudes en contactar un profesor de matematicas a través de nuestra plataforma.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El servicio de emergencia para ciertas áreas rurales de Ohio con frecuencia es un problema, especialmente durante los meses de invierno. El jefe del Departamento de Bomberos de Danville, Township está preocupado por el tiempo de respuesta a las llamadas de emergencia. Ordena una investigación para determinar si la distancia del lugar de la llamada, medida en millas, puede explicar el tiempo de respuesta, medido en minutos.Con base en 37 emergencias, se recolectaron los siguientes datos: ∑X = 234 EY = 831 ∑XY = 5,890
2X*=1.796 2r² =20,037
a. ¿Cuál es el tiempo de respuesta a una llamada que proviene de ocho millas de la estación de bomberos?. ¿Qué tan dependiente es dicha estimación, con base en el grado de dispersión de los puntos de datos alrededor de la recta de regresión?
De una población de 2,500 estudiantes de la universidad Unibe 60% Ingeniería industrial, con un nivel de confianza de 95% y un margen de error de 5%, determine la muestra?
Nota: cuando no conocemos el valor de p y q se les asigna 50% a cada uno y las cantidades que aparecen en porcentaje debe dividirse en 100.
La alcaldía de la ciudad está preocupada por el retiro masivo de las industrias hacía la capital del país, por lo usted como un importante analista en términos económicos lo debe asesorar, se seleccionó una muestra de 500 empresas de las cuales la 300 aún permanecen en la ciudad, la proporción de empresas que han salido de la ciudad se encuentra entre:
Pregunta 5Seleccione una:
a.
40 y 60%
b.
46 y 56%
c.
36 y 44 %
d.
30 y 40 %
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra