Capítulos
Si deseas repasar la teoría de contraste unilateral y contraste bilateral, da click en el link correspondiente.

Contraste unilateral
¿Necesitas clases particulares de matematicas?
Un sociólogo ha pronosticado, que en una determinada ciudad, el nivel de abstención en las próximas elecciones será del 40% como mínimo. Se elige al azar una muestra aleatoria de 200 individuos, con derecho a voto, 75 de los cuales estarían dispuestos a votar. Determinar con un nivel de significación del 1%, si se puede admitir el pronóstico.
1 Enunciamos las hipótesis nula y alternativa:
H0 : μ ≥ 0.40 La abstención será como mínimo del 40%.
H1 : μ < 0.40 La abstención será como máximo del 40%;
2 Zona de aceptación
Para α = 0.01, le corresponde un valor crítico: zα = 2.33.
Determinamos el intervalo de confianza para la media:

3 Verificación
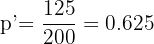
4 Decisión
Aceptamos la hipótesis nula H0. Podemos afirmar, con un nivel de significación del 1%, que la abstención será como mínimo del 40%.
Un informe indica que el precio medio del billete de avión entre Canarias y Madrid es, como máximo, de 120 € con una desviación típica de 40 €. Se toma una muestra de 100 viajeros y se obtiene que la media de los precios de sus billetes es de 128 €.
¿Se puede aceptar, con un nivel de significación igual a 0.1, la afirmación de partida?
1 Enunciamos las hipótesis nula y alternativa:
H0 : μ ≤ 120
H1 : μ > 120
2 Zona de aceptación
Para α = 0.1, le corresponde un valor crítico: zα = 1.28 .
Determinamos el intervalo de confianza:
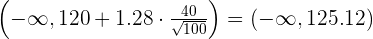
3 Verificación
Valor obtenido de la media de la muestra: 128 €.
4 Decisión
No aceptamos la hipótesis nula H0. Con un nivel de significación del 10%.
Una marca de nueces afirma que, como máximo, el 6% de las nueces están vacías. Se eligieron 300 nueces al azar y se detectaron 21 vacías.
- Con un nivel de significación del 1%, ¿se puede aceptar la afirmación de la marca?
- Si se mantiene el porcentaje muestral de nueces que están vacías y 1-α = 0.95, ¿qué tamaño muestral se necesitaría para estimar la proporción de nueces con un error menor del 1% por ciento?
Inciso 1
1 Enunciamos las hipótesis nula y alternativa:
H0 : p ≤ 0.06
H1 : p >0.06
2 Zona de aceptación
α = 0.01, le corresponde un valor crítico: zα = 2.33.
Determinamos el intervalo de confianza:

3 Verificación
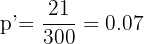
4 Decisión
Aceptamos la hipótesis nula H0. Con un nivel de significación del 1%.
Inciso 2
1 - α = 0.95 z α/2 = 1, 96

Por lo tanto el tamaño muestral mínimo es de n ≥ 2501
La duración de la bombillas de 100 W que fabrica una empresa sigue una distribución normal con una desviación típica de 120 horas de duración. Su vida media está garantizada durante un mínimo de 800 horas. Se escoge al azar una muestra de 50 bombillas de un lote y, después de comprobarlas, se obtiene una vida media de 750 horas. Con un nivel de significación de 0.01, ¿habría que rechazar el lote por no cumplir la garantía?
1 Enunciamos las hipótesis nula y alternativa:
H0 : µ ≥ 800
H1 : µ <800
2 Zona de aceptación
α = 0.01; zα = 2.33
Determinamos el intervalo de confianza:
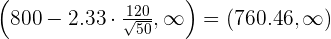
3 Verificación
x = 750
4 Decisión
Rechazamos la hipótesis nula H0. Con un nivel de significación del 1%.
El control de calidad una fábrica de pilas y baterías sospecha que hubo defectos en la producción de un modelo de batería para teléfonos móviles, bajando su tiempo de duración. Hasta ahora el tiempo de duración en conversación seguía una distribución normal con media 300 minutos y desviación típica 30 minutos. Sin embargo, en la inspección del último lote producido, antes de enviarlo al mercado, se obtuvo que de una muestra de 60 baterías el tiempo medio de duración en conversación fue de 290 minutos. Suponiendo que ese tiempo sigue siendo Normal con la misma desviación típica: ¿Se puede concluir que las sospechas del control de calidad son ciertas a un nivel de significación del 2%?
1 Enunciamos las hipótesis nula y alternativa:
H0 : µ ≥ 300
H1 : µ < 300
2 Zona de aceptación
α = 0.02; 1- α = 0. 98; P(1.96)= 0. 98; zα = 1.96 .
Determinamos el intervalo de confianza:

3 Verificación
µ = 290
4 Decisión
Rechazamos la hipótesis nula H0. Con un nivel de significación del 2%.
Contraste bilateral
Un fabricante de lámparas eléctricas está ensayando un nuevo método de producción que se considerará aceptable si las lámparas obtenidas por este método dan lugar a una población normal de duración media 2400 horas, con una desviación típica igual a 300. Se toma una muestra de 100 lámparas producidas por este método y esta muestra tiene una duración media de 2320 horas. ¿Se puede aceptar la hipótesis de validez del nuevo proceso de fabricación con un riesgo igual o menor al 5%?
1 Enunciamos las hipótesis nula y alternativa:
H0 : μ = 2400
H1 : μ ≠2400
2 Zona de aceptación
Para α = 0.05, le corresponde un valor crítico:zα/2 = 1.96.
Determinamos el intervalo de confianza para la media:
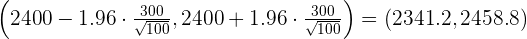
3 Verificación
Valor obtenido de la media de la muestra: 2320 .
4 Decisión
Rechazamos la hipótesis nula H0, con un nivel de significación del 5%.
Se cree que el nivel medio de protombina en una población normal es de 20 mg/100 ml de plasma con una desviación típica de 4 miligramos/100 ml. Para comprobarlo, se toma una muestra de 40 individuos en los que la media es de 18.5 mg/100 ml. ¿Se puede aceptar la hipótesis, con un nivel de significación del 5%?
1 Enunciamos las hipótesis nula y alternativa:
H0 : μ =20 mg/100 ml
H1 : μ ≠ 20 mg/100 ml
2 Zona de aceptación
Para α = 0.05, le corresponde un valor crítico: zα/2 = 1.96.
Determinamos el intervalo de confianza para la media:
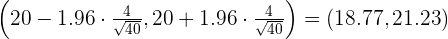
3 Verificación
Valor obtenido de la media de la muestra: 18.5.
4 Decisión
Rechazamos la hipótesis nula H0, con un nivel de significación del 5%.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El servicio de emergencia para ciertas áreas rurales de Ohio con frecuencia es un problema, especialmente durante los meses de invierno. El jefe del Departamento de Bomberos de Danville, Township está preocupado por el tiempo de respuesta a las llamadas de emergencia. Ordena una investigación para determinar si la distancia del lugar de la llamada, medida en millas, puede explicar el tiempo de respuesta, medido en minutos.Con base en 37 emergencias, se recolectaron los siguientes datos: ∑X = 234 EY = 831 ∑XY = 5,890
2X*=1.796 2r² =20,037
a. ¿Cuál es el tiempo de respuesta a una llamada que proviene de ocho millas de la estación de bomberos?. ¿Qué tan dependiente es dicha estimación, con base en el grado de dispersión de los puntos de datos alrededor de la recta de regresión?
De una población de 2,500 estudiantes de la universidad Unibe 60% Ingeniería industrial, con un nivel de confianza de 95% y un margen de error de 5%, determine la muestra?
Nota: cuando no conocemos el valor de p y q se les asigna 50% a cada uno y las cantidades que aparecen en porcentaje debe dividirse en 100.
La alcaldía de la ciudad está preocupada por el retiro masivo de las industrias hacía la capital del país, por lo usted como un importante analista en términos económicos lo debe asesorar, se seleccionó una muestra de 500 empresas de las cuales la 300 aún permanecen en la ciudad, la proporción de empresas que han salido de la ciudad se encuentra entre:
Pregunta 5Seleccione una:
a.
40 y 60%
b.
46 y 56%
c.
36 y 44 %
d.
30 y 40 %
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra