Capítulos

¿Qué es el muestreo?
Supongamos que tenemos una población  de objetos o individuos que queremos estudiar, la cual puede ser finita o infinita. En muchas situaciones, es imposible estudiar a cada uno de los individuos de esta población.
de objetos o individuos que queremos estudiar, la cual puede ser finita o infinita. En muchas situaciones, es imposible estudiar a cada uno de los individuos de esta población.
Para resolver este problema, se suele extraer una muestra de la población. Una muestra es un subconjunto  de la población, es decir,
de la población, es decir, 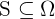 . Existen varios métodos para obtener una muestra de la población. Sin embargo, el objetivo de cualquier método es que la muestra sea representativa de la población, es decir, que las propiedades de la muestra sean muy similares a las propiedades de la población.
. Existen varios métodos para obtener una muestra de la población. Sin embargo, el objetivo de cualquier método es que la muestra sea representativa de la población, es decir, que las propiedades de la muestra sean muy similares a las propiedades de la población.
Una vez que tenemos una muestra, se utiliza la inferencia estadística para obtener conclusiones sobre la población. Así, la inferencia estadística es el conjunto de procedimientos que se utilizan para "inferir" propiedades de la población a partir de una muestra dada.
Además, la inferencia estadística también nos da herramientas que nos sirven para determinar el grado de fiabilidad o confianza de nuestras conclusiones.
En general, las técnicas de muestreo se dividen en dos categorías: muestreo no estadístico y muestreo probabilístico.
Muestreo no estadístico
Los métodos de muestreo no estadístico no utilizan la probabilidad (o el azar) para elegir los elementos de la muestra.
Debido a que no utilizan la probabilidad, estos métodos no garantizan que la muestra sea representativa. Por tanto, deben utilizarse con cuidado para evitar sesgos en las conclusiones. Asimismo, estos métodos son susceptibles a sub-representación y sobre-representación de sub-grupos en la población.
No obstante, estos métodos tienen algunas ventajas. La ventaja más importante es que son más sencillos de utilizar que las técnicas probabilísticas. Además, suele ser más barato obtener una muestra con estas técnicas y, en muchos casos, es la única forma que tenemos para obtener la muestra.
Es por estos motivos que estas técnicas de muestreo suelen utilizarse principalmente en las "pruebas piloto" antes de utilizar técnicas estadísticas más sofisticadas.
Algunos ejemplos de técnicas de muestreo no estadístico son:
1 Muestreo de conveniencia: involucra tomar como muestra a aquellos individuos de la población que tenemos cerca. También se conoce como muestreo de oportunidad.
Por ejemplo, podemos estudiar las preferencias electorales de nuestra ciudad entrevistando a las personas que viven en nuestra colonia. En este caso la población son lo habitantes de la ciudad y la muestra son los habitantes de nuestra colonia.
2 Muestreo experto: en este caso la muestra se selecciona a partir de la opinión de un experto. También se conoce como muestreo a juicio. Es importante notar que este método se puede combinar con un procedimiento aleatorio; sin embargo, es necesario cuidar que el juicio no introduzca sesgos.
Por ejemplo, para estudiar las preferencias electorales de nuestra ciudad, un experto nos sugiere que las colonias  ,
,  y
y  suelen representar mejor la opinión general de la ciudad. Por tanto, sólo entrevistamos a los habitantes de estas colonias.
suelen representar mejor la opinión general de la ciudad. Por tanto, sólo entrevistamos a los habitantes de estas colonias.
Muestreo probabilístico
En el muestreo probalístico se eligen la muestra de forma aleatoria. De esta forma, cada individuo de la población tiene una probabilidad conocida de ser seleccionado. Esto permite que cada individuo tenga la posibilidad de seleccionado y reduce la probabilidad de introducir sesgos en nuestras conclusiones.
Cada método tiene sus propias ventajas y desventajas. Las más comunes se listan a continuación.
Si necesitas ayuda, no dudes en recurrir a nuestras clases particulares de matematicas.
Muestreo aleatorio simple
En el muestreo aleatorio simple, cada individuo de la población tiene la misma probabilidad de ser seleccionado para la muestra.
Una forma de realizar este muestreo es numerar los elementos de la población y luego seleccionar al azar  elementos. Sin embargo, existen dos formas de realizar este muestreo:
elementos. Sin embargo, existen dos formas de realizar este muestreo:
1 Muestreo con reemplazo: una vez que seleccionamos un elemento, el mismo elemento puede volver a ser seleccionado cuando se toma el siguiente elemento. Por lo tanto, es posible que algún individuo pertenezca más de una vez en la muestra.
Aunque es posible que un elemento se repita más de una vez en la muestra, esto no suele ser un inconveniente en las conclusiones que hagamos. Además, tiene la ventaja de que facilita los cálculos de las inferencias.
2 Muestreo sin reemplazo: en este caso, una vez que seleccionamos un elemento, entonces lo descartaremos cuando escojamos el resto de los elementos. Así, cada elemento puede ser seleccionado máximo una vez.
Este método tiene la ligera ventaja de que cada elemento sea seleccionado máximo una vez. Sin embargo, esto hace que algunos cálculos y estimaciones sean ligeramente más complicados.
Ejemplo: en el mismo ejemplo de las preferencias electorales en una ciudad, seleccionamos al azar  números del registro de vivienda. Entonces se entrevistan a las familias de esas viviendas.
números del registro de vivienda. Entonces se entrevistan a las familias de esas viviendas.
Observemos que el costo de este tipo de muestreo es ligeramente más alto, ya que tendríamos que visitar hogares de un número grande de colonias.
Muestreo aleatorio sistemático
Supongamos que tenemos una población  elementos que están numerados del 1 a
elementos que están numerados del 1 a  y queremos elegir una muestra que sea una
y queremos elegir una muestra que sea una  -ésima parte de la población.
-ésima parte de la población.
Entonces seleccionamos un número  al azar entre 1 y
al azar entre 1 y  . El resto de los elementos los elegimos a intervalos constantes (de tamaño
. El resto de los elementos los elegimos a intervalos constantes (de tamaño  ) hasta completar la muestra. Por tanto, nuestra muestra consiste en los elementos
) hasta completar la muestra. Por tanto, nuestra muestra consiste en los elementos

Ejemplo: si tenemos una población de 1000 individuos y deseamos extraer una población de 25 elementos, entonces la razón  es
es

Luego, escogemos un número entre 1 y 40 (supongamos que el número aleatorio es 24). Así, la muestra consiste de los elementos
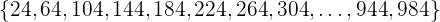
Este método tiene la ventaja de que la muestra se distribuye de una forma más "uniforme" sobre toda la población.
Muestreo aleatorio estratificado
Supongamos que la población se divide naturalmente en  sub-poblaciones, y denotemos el tamaño de cada una mediante
sub-poblaciones, y denotemos el tamaño de cada una mediante  ,
,  , ...,
, ..., 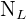 . Estas sub-poblaciones se conocen como estratos.
. Estas sub-poblaciones se conocen como estratos.
En el muestreo estratificado es importante que los estratos no se superpongan. Es decir, que no exista ningún elemento que pertenezca a más de un estrado. Además, es importante todos los elementos pertenezcan a un estrado.
El muestreo estratificado consiste en realizar un muestreo aleatorio simple dentro de cada estrato. Es decir, consideramos a cada estrato como una población para formar nuestra muestra global. El muestreo estratificado puede permitirnos realizar estimaciones más precisas de la población, aunque esto requiere de cálculos un poco más complicados.
El principal problema del muestreo estratificado consiste en determinar el tamaño de muestra dentro de cada estrato. Existen dos estrategias:
1 Asignación proporcional: en este caso, si el tamaño de muestra global es de  , entonces el tamaño de muestra de cada estrato es
, entonces el tamaño de muestra de cada estrato es
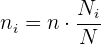
Esta estrategia tiene la ventaja de que cada estrato está representado de forma proporcional.
2 Asignación óptima: en este caso buscamos minimizar la varianza de las estimaciones dentro de cada estrato. Así, aquellos estratos con menos varianza tienen tamaños muestrales más pequeños.
Esta estrategia tiene la ventaja de que podemos hacer estimaciones mucho más precisas.
Ejemplo: En una fábrica que consta de 600 trabajadores queremos tomar una muestra de 20. Sabemos que hay 200 trabajadores en la sección  , 150 en la
, 150 en la  , 150 en la
, 150 en la  y 100 en la
y 100 en la  .
.
Si se decide utilizar un muestreo estratificado con asignación proporcional, ¿qué tamaño tendrá cada estrato?
Denotemos como  al tamaño de la población y
al tamaño de la población y  al tamaño de la muestra general. Similarmente, denotamos como
al tamaño de la muestra general. Similarmente, denotamos como 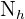 al tamaño del estrato
al tamaño del estrato  y
y  al tamaño de muestra que tomamos de
al tamaño de muestra que tomamos de  . De este modo, como tenemos asignación proporcional, se cumple
. De este modo, como tenemos asignación proporcional, se cumple
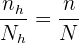
El problema se trata únicamente de encontrar los valores n_h para cada estrato. Observemos que ya conocemos el tamaño de la población 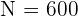 ; los tamaños de cada estrato
; los tamaños de cada estrato 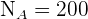 ,
, 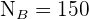 ,
, 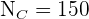 y
y 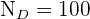 .
.
Además, sabemos que 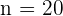 , por lo que ya tenemos todos los datos para calcular el tamaño de muestra para cada estrato. Primero despejamos
, por lo que ya tenemos todos los datos para calcular el tamaño de muestra para cada estrato. Primero despejamos  :
:
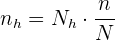
Así, para la sección A debemos tomar:

Para la sección B:
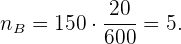
Para la sección C:
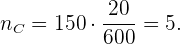
Por último, para la sección D:

Por último, verificamos que

Sin embargo, si deseamos estimar el peso de los trabajadores y en la sección  trabajan solo modelos que sabemos que tienen bajo peso, entonces podríamos elegir sólo 2 individuos de la sección
trabajan solo modelos que sabemos que tienen bajo peso, entonces podríamos elegir sólo 2 individuos de la sección  y el resto de las secciones
y el resto de las secciones  ,
,  y
y  . No obstante, el tamaño muestral se debe escoger con base en alguna información previa que tengamos de la varianza.
. No obstante, el tamaño muestral se debe escoger con base en alguna información previa que tengamos de la varianza.
Muestreo aleatorio por conglomerados
En el muestreo por conglomerados asumimos que la población también se divide en  estratos. En el muestreo por conglomerados, estos estratos se conocen como grupos, clústers o conglomerados.
estratos. En el muestreo por conglomerados, estos estratos se conocen como grupos, clústers o conglomerados.
Si denotamos los grupos como 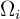 , entonces el muestreo por conglomerados consiste en seleccionar algunos de estos grupos y estos grupos formaran nuestra muestra. En otras palabras, consideramos cada grupo como un elemento y hacemos una muestra aleatoria de grupos.
, entonces el muestreo por conglomerados consiste en seleccionar algunos de estos grupos y estos grupos formaran nuestra muestra. En otras palabras, consideramos cada grupo como un elemento y hacemos una muestra aleatoria de grupos.
Este tipo de muestreo tiene la ventaja de que puede ser más barato y más sencillo que los otros tipos de muestreo, mientras que conserva la aleatoriedad del muestreo probabilístico.
Ejemplo: si deseáramos estudiar las preferencias electorales de una ciudad, en lugar realizar muestreo aleatorio simple podemos elegir de forma aleatoria algunas colonias. Esto nos da la ventaja de que tenemos una muestra más representativa en comparación con un muestreo de conveniencia. Además, el costo es menor comparado con el muestreo aleatorio simple, pues en lugar de visitar todas las colonias, sólo debemos visitar un cantidad pequeña de colonias.
Distribución de los parámetros muestrales
Dada una población  , existe un gran número de muestras de tamaño
, existe un gran número de muestras de tamaño  . Supongamos que deseamos saber el valor de un parámetro
. Supongamos que deseamos saber el valor de un parámetro  de la población, entonces cada una de esas poblaciones dará una estimación
de la población, entonces cada una de esas poblaciones dará una estimación  de ese parámetro.
de ese parámetro.
Si se realiza un muestreo apropiado, entonces la mayoría de esas estimaciones serán cercanas a  . Sin embargo, notemos que
. Sin embargo, notemos que  dependerá de la muestra que se haya tomado.
dependerá de la muestra que se haya tomado.
A la distribución de todos los posibles valores de  se le conoce como distribución muestral de
se le conoce como distribución muestral de  . Si conocemos esta distribución, entonces podemos hacer conclusiones del parámetro poblacional
. Si conocemos esta distribución, entonces podemos hacer conclusiones del parámetro poblacional  .
.
Los parámetros poblacionales que se estudian con más frecuencia son la media  , la varianza
, la varianza 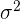 (o desviación estándar
(o desviación estándar  ) y la proporción
) y la proporción  .
.
Teorema central del límite
El teorema central del límite es uno de los teoremas más importantes de la estadística, pues nos permite utilizar la distribución normal para hacer estimaciones de poblaciones que no siguen la distribución normal. Este teorema es uno de los motivos por el cual la distribución normal es muy importante.
Teorema (central del límite). Consideremos la muestra  de tamaño
de tamaño  tomada de la población
tomada de la población  utilizan muestreo aleatorio simple. Sea
utilizan muestreo aleatorio simple. Sea  la media y
la media y  la desviación estándar de
la desviación estándar de  . Si el tamaño de muestra es suficientemente grande, entonces la media muestral
. Si el tamaño de muestra es suficientemente grande, entonces la media muestral  sigue aproximadamente una distribución normal con media
sigue aproximadamente una distribución normal con media  y desviación estándar
y desviación estándar  . Además, entre más grande es el tamaño de la muestra, mejor se aproxima a la distribución normal.
. Además, entre más grande es el tamaño de la muestra, mejor se aproxima a la distribución normal.
Una regla general para que el tamaño de muestra sea "suficientemente grande" es que  . Por tanto, si
. Por tanto, si  entonces podemos utilizar el teorema central del límite con seguridad.
entonces podemos utilizar el teorema central del límite con seguridad.
Las consecuencias más importantes del teorema central del límite son:
1 Si ya conocemos la media  y desviación estándar
y desviación estándar  de la población, entonces podemos conocer la probabilidad de que la media muestral esté en cierto intervalo.
de la población, entonces podemos conocer la probabilidad de que la media muestral esté en cierto intervalo.
2 Si asumimos que la media  de la población es
de la población es 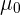 , entonces podemos conocer, a priori, en qué intervalo estará la media muestral. Luego, si la media muestral no está en ese intervalo, tendremos evidencia de que nuestra asunción era incorrecta.
, entonces podemos conocer, a priori, en qué intervalo estará la media muestral. Luego, si la media muestral no está en ese intervalo, tendremos evidencia de que nuestra asunción era incorrecta.
3 De manera similar al caso anterior, podemos saber, a priori, en qué intervalo estará la suma de los elementos de una muestra. La suma de los elementos sigue la distribución dada por
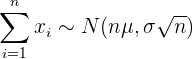
Ejemplo: Las bolsas de sal envasadas por una máquina tienen un peso promedio de  con una desviación estándar de
con una desviación estándar de 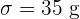 . Las bolsas se empaquetaron en cajas de 100 unidades.
. Las bolsas se empaquetaron en cajas de 100 unidades.
a Calcular la probabilidad de que la media de los pesos de las bolsas de un paquete sea menor que 495 g.
b Calcular la probabilidad de que una caja de 100 bolsas pese más de 51 kg.
a Para responder la primera pregunta, debemos recordar que el promedio de una muestra de tamaño  sigue aproximadamente una distribución normal (debido al teorema central del límite), es decir,
sigue aproximadamente una distribución normal (debido al teorema central del límite), es decir,
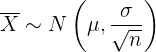
Por tanto, el promedio de las bolsas en cada caja seguirá una distribución
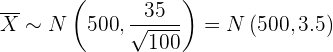
Así, para calcular la probabilidad utilizamos
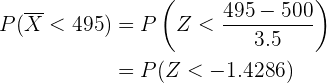
donde  es una variable aleatoria con distribución normal estándar.
es una variable aleatoria con distribución normal estándar.
Esta probabilidad se puede calcular de varias maneras, por ejemplo, utilizar Excel o un lenguaje de programación como R.
Otra forma de calcular esta probabilidad, es utilizando una tabla de probabilidades de la distribución normal, para ello necesitamos escribir la probabilidad de la siguiente manera:

y ya podemos buscar 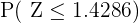 en una tabla distribución normal, donde tenemos que
en una tabla distribución normal, donde tenemos que 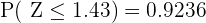 (es el valor más cercano, pues sólo tiene precisión de 2 cifras). Así,
(es el valor más cercano, pues sólo tiene precisión de 2 cifras). Así,
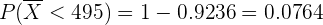
Si utilizamos un lenguaje de programación, el resultado es
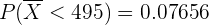
que es bastante similar.
b Este inciso es similar al anterior. La única diferencia es que ahora la variable aleatoria es la suma de los 100 elementos de la muestra. En este caso, por el teorema central del límite, tenemos
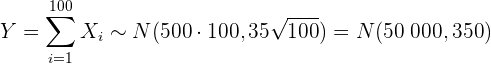
donde  es el peso de la caja en gramos. De este modo, la probabilidad que buscamos es
es el peso de la caja en gramos. De este modo, la probabilidad que buscamos es 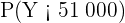 , pues 51 kg es igual a 51 000 g.
, pues 51 kg es igual a 51 000 g.
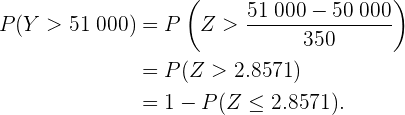
Así, si utilizamos una tabla de distribución normal, el resultado es
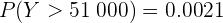
mientras que si utilizamos una Excel o un lenguaje de programación, el resultado da

Recordemos que el resultado obtenido con computadora es más preciso.
Intervalos característicos
Dada una variable aleatoria  , el intervalo característico
, el intervalo característico 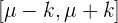 se calcula como aquel intervalo tal que
se calcula como aquel intervalo tal que
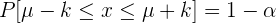
Estos intervalos son importantes para realizar estimaciones e intervalos de confianza. En este contexto, se suelen utilizar los siguientes términos:
1 Nivel de confianza: 
2 Significancia o nivel de significación: 
3 Valor crítico: 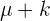 o
o  .
.
Notemos que se denotó  a
a 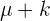 . Esto ocurre cuando calculamos un intervalo característico de una distribución normal estándar
. Esto ocurre cuando calculamos un intervalo característico de una distribución normal estándar  .
.
Ejemplo: Encuentra el intervalo característico de una distribución normal  correspondiente a una confianza de
correspondiente a una confianza de 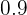 .
.
Observa la siguiente imagen:

Notemos que 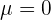 , de modo que el intervalo tendrá la forma
, de modo que el intervalo tendrá la forma 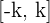 o
o 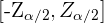 . Por tanto, las colas del lado izquierdo y derecho tienen una probabilidad de 0.05 (es decir,
. Por tanto, las colas del lado izquierdo y derecho tienen una probabilidad de 0.05 (es decir, 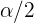 ). Así, basta con encontrar el valor
). Así, basta con encontrar el valor  tal que
tal que
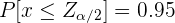
Esto se puede hacer de varias maneras: se puede utilizar una tabla normal o se puede utilizar el comando  del lenguaje de programación R.
del lenguaje de programación R.
Sin importar el método que utilicemos, obtendríamos que  . Así, el intervalo característico a una confianza del 90% es
. Así, el intervalo característico a una confianza del 90% es
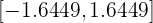
Tabla de valores críticos
En la tabla de abajo de encuentran valores críticos para la distribución normal estándar  para unos niveles comunes de confianza:
para unos niveles comunes de confianza:
 | 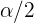 |  |
|---|---|---|
| 0.90 | 0.05 | 1.6448 |
| 0.95 | 0.025 | 1.9600 |
| 0.99 | 0.005 | 2.5758 |
Si trabajamos con una distribución normal 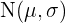 , entonces los intervalos críticos se pueden calcular a partir de los valores críticos de la distribución
, entonces los intervalos críticos se pueden calcular a partir de los valores críticos de la distribución  como se muestra a continuación:
como se muestra a continuación:
 | 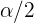 |  | Intervalos característicos |
|---|---|---|---|
| 0.90 | 0.05 | 1.6449 | 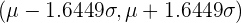 |
| 0.95 | 0.025 | 1.9600 | 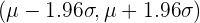 |
| 0.99 | 0.005 | 2.5758 |  |
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El servicio de emergencia para ciertas áreas rurales de Ohio con frecuencia es un problema, especialmente durante los meses de invierno. El jefe del Departamento de Bomberos de Danville, Township está preocupado por el tiempo de respuesta a las llamadas de emergencia. Ordena una investigación para determinar si la distancia del lugar de la llamada, medida en millas, puede explicar el tiempo de respuesta, medido en minutos.Con base en 37 emergencias, se recolectaron los siguientes datos: ∑X = 234 EY = 831 ∑XY = 5,890
2X*=1.796 2r² =20,037
a. ¿Cuál es el tiempo de respuesta a una llamada que proviene de ocho millas de la estación de bomberos?. ¿Qué tan dependiente es dicha estimación, con base en el grado de dispersión de los puntos de datos alrededor de la recta de regresión?
De una población de 2,500 estudiantes de la universidad Unibe 60% Ingeniería industrial, con un nivel de confianza de 95% y un margen de error de 5%, determine la muestra?
Nota: cuando no conocemos el valor de p y q se les asigna 50% a cada uno y las cantidades que aparecen en porcentaje debe dividirse en 100.
La alcaldía de la ciudad está preocupada por el retiro masivo de las industrias hacía la capital del país, por lo usted como un importante analista en términos económicos lo debe asesorar, se seleccionó una muestra de 500 empresas de las cuales la 300 aún permanecen en la ciudad, la proporción de empresas que han salido de la ciudad se encuentra entre:
Pregunta 5Seleccione una:
a.
40 y 60%
b.
46 y 56%
c.
36 y 44 %
d.
30 y 40 %
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra