Capítulos

¿Qué es el rango de una matriz?
Hay varias definiciones equivalentes de lo que es el rango de una matriz. Al rango de una matriz 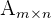 de dimensión
de dimensión 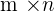 lo denotamos como
lo denotamos como 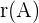 ,
,  o, en inglés,
o, en inglés, 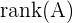 .
.

Dimensión del espacio columna o espacio fila
Quizá lo más común en ingeniería es definir el rango como el número de filas (o columnas) linealmente independientes, esto debido a que es fácil obtener las filas linealmente independientes de una matriz utilizando el método de Gauss o el método de Gauss-Jordan.
Ejemplo:
Consideremos la matriz  dada por
dada por
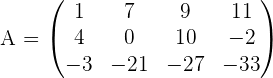
Notemos que la primer fila,  , y la segunda,
, y la segunda,  , son linealmente independientes, ya que
, son linealmente independientes, ya que
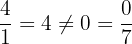
sin embargo, la primer fila y la tercer fila,  , son linealmente independientes, esto ta que
, son linealmente independientes, esto ta que  . Por lo tanto, tenemos dos filas linealmenteindependiente de las tres que constituyen la matriz. Dicho lo anterior, el rango de
. Por lo tanto, tenemos dos filas linealmenteindependiente de las tres que constituyen la matriz. Dicho lo anterior, el rango de  es
es 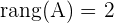 .
.
Nota. Puedes visitar este artículo para aprender el método de Gauss.
Ejemplo:
Ahora aplicaremos el método de Gauss para obtener el rango de la matriz del ejemplo anterior.
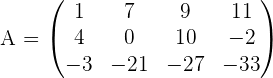
Aplicando el método de Gauss tenemos que
Al finalizar nuestro proceso tenemos que nuestra matriz resultante es
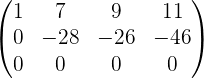
Como terminamos con dos filas no nulas, tenemos que el rango es 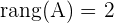 .
.
Rango por determinantes
Podemos definir el rango de una matriz como el orden de la mayor submatriz cuadrada no nula de nuestra matriz  . Utilizando esta definición se puede calcular el rango usando determinantes, sin embargo, no es un método muy recomendable dado que puede llegar a ser demasiado tardado y, dependiendo la dimensión de la matriz, incluso complicado el cálculo de algunos determinantes.
. Utilizando esta definición se puede calcular el rango usando determinantes, sin embargo, no es un método muy recomendable dado que puede llegar a ser demasiado tardado y, dependiendo la dimensión de la matriz, incluso complicado el cálculo de algunos determinantes.
Nota. Puedes visitar este artículo para aprender el método por determinantes.
Ejemplo:
Consideremos la siguiente matriz
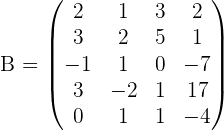
Procedamos con los pasos:
1 Suprimimos la tercera columna porque es combinación lineal de las dos primeras, 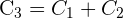
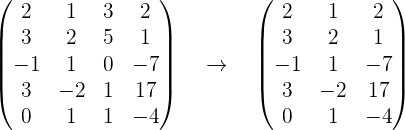
2 Comprobamos si tiene rango mayor o igual que uno, para ello se tiene que cumplir que al menos un elemento de la matriz no sea cero y por tanto su determinante no será nulo. Notemos que, al ser la matriz no nula, tenemos que
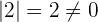 .
.
Por lo tanto su rango es igual o mayor que uno.
3 Tendrá rango mayor o igual que dos si existe alguna submatriz cuadrada de orden 2, tal que su determinante no sea nulo. Notemos que
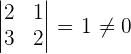
4 Tendrá rango mayor o igual que tres si existe alguna submatriz cuadrada de orden 3, tal que su determinante no sea nulo. En este caso, calculando los determinantes de todas las submatrices de dimensión 3, tenemos que
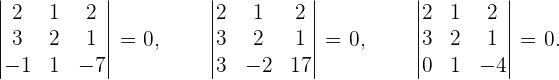
Como todos los determinantes de las submatrices son nulos, tienen rango menor que tres, por tanto  .
.
Dimensión del espacio imagen
Esta definición de rango de una matriz es un poco más matemática y complicada de comprender, sin embargo, no está mal tenerla como dato. Aquí necesitamos tener noción del concepto de aplicaciones lineales. Esto ya que, por teoría de álgebra lineal, dada una matriz  , existe una única aplicación lineal asociada,
, existe una única aplicación lineal asociada,
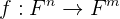 ,
,
definida como
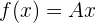 ,
,
entonces, el rango de 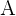 es la dimensión de la imagen de
es la dimensión de la imagen de 
(como espacio vectorial).
No es necesario dominar esta definición ya que solo suele utilizarse en matemáticas puras o física, sin embargo, podemos tenerla como dato general.
Resumir con IA:










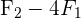
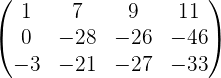




Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio 4 de ecuaciones matriciales se confunden y ponen la matriz C en el lugar de la B y viceversa, pensaba que era error mio de calculo pero creo que esta mal la solucion de ustedes, por el resto me ayudo mucho
Hola revise lo que mencionaste, si había un error pero ya se corrigió, lo que mencionas no lo encontré, podrías revisar y mencionarlo por favor.
Hola, una disculpa por el error, ya se corrigió.
Un número real por una matriz creo que no es el número real por cada elemento de una matriz, sino por los elementos de una sola fila o columna, esto en lo cierto?
Hola el algebra matricial es muy amplia en conceptos, pero lo principal es que una matriz representa arreglos que superan a un solo número real, es como un universo mas amplio que la idea de un solo número real, si no fui claro por favor indícamelo para mejorar.
Muchas gracias , me ayudan mucho con mi examen, solo tenia una duda, en el ejercicio 2 de Sistemas de ecuaciones con matrices, me sale que Y= 8/5, no se en que estoy fallando o creo que se confundieron de símbolo en el elemento de la fila 2 columna 1 de la matriz inversa , debería ser 2/5 y no -2/5.
Hola tienes toda la razón, una disculpa ya se corrigió el error.
Hola, gracias por esto, bien explicado. Por favor, me gustaría también ―pues vengo de las Humanidades― una historia de las matrices. Cómo se inventaron, por quién ; qué necesidad resolvían y no estaba bien cubierta antes. He leído que fueron importantes en aeronáutica. Enhorabuena. ¡Gracias!
Lo tendremos en consideración para nuestro blog 😊 Gracias por tu aporte. Un saludo.
Como resolver 1/2 AB EN MATRICES