Capítulos
Una matriz 
es la inversa de una matriz 
si cumple que
.
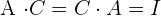Para denotar la inversa de escribimos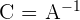 
.
Propiedades de la matriz inversa
1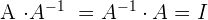 
2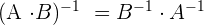 
3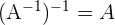 
4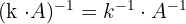 
5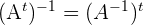 
Cálculo de la matriz inversa por determinantes
Se realiza aplicando la siguiente fórmula
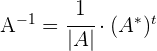
donde:
es el determinante de la matriz
es la matriz adjunta
es la matriz traspuesta de la adjunta
Ejemplo: Hallar por determinantes la matriz inversa de:
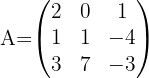
1 Obtenemos la determinante
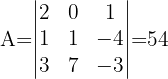
2 Obtenemos la matriz adjunta
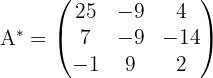
3 Obtenemos la matriz traspuesta de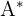 
4 Aplicamos la fórmula para hallar la inversa con determinantes y obtenemos
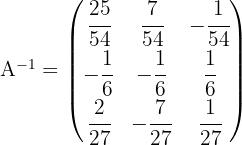
Cálculo por el método de Gauss
Sea una matriz cuadrada de orden 
. Para calcular la matriz inversa de , que denotaremos como 
, seguiremos los siguientes pasos:
1 Construir una matriz del tipo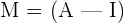 
, es decir, está en la mitad izquierda de 
y la matriz identidad 
en la derecha.
2 Utilizando el método Gauss vamos a transformar la mitad izquierda , en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa .
Ejemplo: Hallar por el método de Gauss la matriz inversa de:
1 Construir una matriz del tipo 
2 Utilizamos el método Gauss
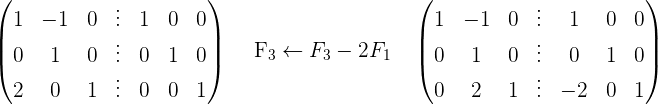
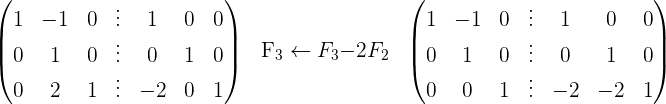
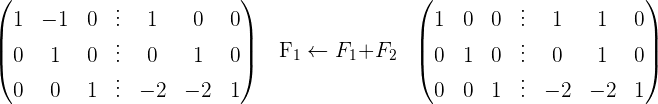
3 La matriz inversa es
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio 4 de ecuaciones matriciales se confunden y ponen la matriz C en el lugar de la B y viceversa, pensaba que era error mio de calculo pero creo que esta mal la solucion de ustedes, por el resto me ayudo mucho
Hola revise lo que mencionaste, si había un error pero ya se corrigió, lo que mencionas no lo encontré, podrías revisar y mencionarlo por favor.
Hola, una disculpa por el error, ya se corrigió.
Un número real por una matriz creo que no es el número real por cada elemento de una matriz, sino por los elementos de una sola fila o columna, esto en lo cierto?
Hola el algebra matricial es muy amplia en conceptos, pero lo principal es que una matriz representa arreglos que superan a un solo número real, es como un universo mas amplio que la idea de un solo número real, si no fui claro por favor indícamelo para mejorar.
Muchas gracias , me ayudan mucho con mi examen, solo tenia una duda, en el ejercicio 2 de Sistemas de ecuaciones con matrices, me sale que Y= 8/5, no se en que estoy fallando o creo que se confundieron de símbolo en el elemento de la fila 2 columna 1 de la matriz inversa , debería ser 2/5 y no -2/5.
Hola tienes toda la razón, una disculpa ya se corrigió el error.
Hola, gracias por esto, bien explicado. Por favor, me gustaría también ―pues vengo de las Humanidades― una historia de las matrices. Cómo se inventaron, por quién ; qué necesidad resolvían y no estaba bien cubierta antes. He leído que fueron importantes en aeronáutica. Enhorabuena. ¡Gracias!
Lo tendremos en consideración para nuestro blog 😊 Gracias por tu aporte. Un saludo.
Como resolver 1/2 AB EN MATRICES