Capítulos
¿Que es el algoritmo de Euclides?
El algoritmo de Euclides es un procedimiento para calcular el máximo común divisor (m.c.d.) de dos números.
Euclides fue un matemático griego que recopiló varios datos en una obra llamada Elementos. Esta obra es considerada como uno de los pillares de las matemáticas, y Euclides el "padre de la geometría".
En Elementos, Euclides explica que el máximo común divisor de dos números se puede encontrar dividiendo el número mayor por el número menor. Si la división es exacta, el m.c.d. es el número menor. Si la división no es exacta, entonces se toma el residuo, y se divide tantas veces como haga falta para llegar a una división sin residuo. El m.c.d. es el último número por cuál se puede dividir.
Aunque la palabra algoritmo nos hace pensar en cálculos complejos resueltos por ordenadores, en nuestro caso el cálculo es mucho más sencillo. Solo hace falta seguir los siguientes pasos.
Pasos del algoritmo de Euclides
1 Se divide el número mayor entre el menor.
2 Si la división es exacta, el divisor es el m.c.d.
3Si la división no es exacta, dividimos el divisor entre el resto obtenido y continuamos de esta forma hasta obtener una división exacta. El m.c.d. es el último divisor.
Ejemplos de aplicación del algoritmo de Euclides
Encontrar el m.c.d de 
y 
Encontrar el m.c.d de y El primer paso es dividir por :
Multiplicamos el número por la parte entera del resultado 
, es decir por 
:
Sustrayemos el número 
del y obtenemos:
Repetimos los pasos, tomando el divisor, el número y dividiéndolo por el resto obtenido 
:
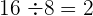
El m.c.d. de y es el último divisor cual nos da un resultado exacto, el .
Encontrar el m.c.d de 
y 
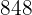
Encontrar el m.c.d de y 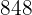Aplicamos los mismos pasos que en el ejemplo anterior.
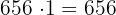
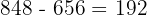
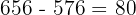
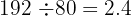
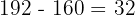
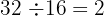
El m.c.d. siendo el último divisor, este es
Encontrar el m.c.d. de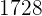 
y 
Encontrar el m.c.d. de 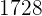y Siguiendo los mismos pasos empezamos los cálculos:
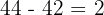
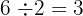
El m.c.d. de 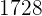y es 
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)