Capítulos

Los números primos son aquellos números naturales que solamente se pueden dividir por sí mismos y por 1, es decir, que si intentamos dividirlos por cualquier otro número, el resultado no es entero.

Algunos números primos son

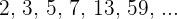
El número 1 sólo tiene un divisor, que es él mismo, por eso no es considerado como un número primo.

Para demostrar que un número es primo, se divide ordenadamente por todos los números primos menores que él. Cuando, sin resultar divisiones exactas, llega a obtenerse un cociente menor o igual al divisor, podremos afirmar que el número en cuestión es primo.

Ejemplo: determinar si el número 179 es primo.

Para determinar si      es número primo, deberemos dividirlo entre todos los primos menores a él (ordenados de forma ascendente) hasta obtener un cociente menor o igual al respectivo divisor.

Comencemos con la división por     Para este caso, analicemos la expresión siguiente,

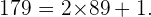
De la igualdad anterior se sigue que, al dividir    por 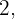    obtenemos como cociente al número  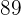  y como residuo a  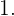    Esto significa que la división de      por      no da como resultado un número entero, pues el residuo es distinto de cero.

Ahora procedemos a hacer lo mismo pero con los números primos siguientes: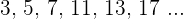

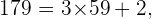
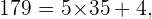
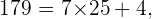
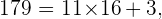
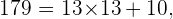
En este último caso hemos encontrado que el cociente de dividir      por      es      que es menor a 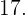     Como además esta división tiene residuo distinto de cero, es equivalente a decir que no tiene como resultado a un número entero. Además, es necesario notar que ninguna de las divisiones entre los demás números primos ha dado como resultado un número entero.

Con estos argumentos, podemos afirmar que es nun número primo.

La criba de Eratóstenes es un algoritmo que permite hallar números primos menores a un número natural dado.

Los pasos de tal algoritmo son los siguientes:

1Partimos de una lista de números que van de    hasta un determinado número.

2 Eliminamos de la lista los múltiplos de  

3 Tomamos el primer número después del nbsp;  que no fue eliminado (el   )  y eliminamos de la lista sus múltiplos, y continuamos de manera iterativa.

4 El proceso termina cuando el cuadrado del mayor número confirmado como primo es menor que el número final de la lista.

Como resultado, los números que permanecen en la lista son los primos.

Ejemplo: encontrar todos los números primos menores a 40.

1 - Como primer paso, escribimos todos los números comprendidos entre      y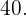   

2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40

2 - Ahora, eliminemos los múltiplos de  

2 3 5 7 9
11 13 15 17 19
21 23 25 27 29
31 33 35 37 39

3 - El siguiente número es    y como 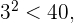    eliminamos también los múltiplos de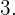  

2 3 5 7
11 13 15 17 19
23 25 29
31 35 37

4 - El siguiente número es      y dado que      eliminamos los múltiplos de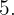   

2 3 5 7
11 13 17 19
23 29
31 37

5 - Por último, tenemos que el siguiente número es 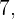     sin embargo  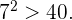    Por tanto, podemos terminar el algoritmo y concluir que los números que quedan han de ser primos.

2 3 5 7
11 13 17 19
23 29
31 37

Tabla de números primos hasta 1000

2357111317192329
31374143475359616771
7379838997101103107109113
127131137139149151157163167173
179181191193197199211223227229
233239241251257263269271277281
283293307311313317331337347349
353359367373379383389397401409
419421431433439443449457461463
467479487491499503509521523541
547557563569571577587593599601
607613617619631641643647653659
661673677683691701709719727733
739743751757761769773787797809
811821823827829839853857859863
877881883887907911919929937941
947953967971977983991997//

¿Te ha gustado este artículo? ¡Califícalo!

4,23 (90 nota(s))
Cargando...

Marta

➗ Licenciada en Químicas da clase de Matemáticas, Física y Química -> Comparto aquí mi pasión por las matemáticas ➗