El mínimo común múltiplo (MCM) y el máximo común divisor (MCD) son conceptos fundamentales en la teoría de números, utilizados para resolver una amplia variedad de problemas en matemáticas, desde fracciones hasta problemas de optimización en diversas áreas. Estos dos conceptos nos permiten comparar y relacionar números de manera efectiva, lo que facilita el trabajo con expresiones algebraicas y problemas numéricos.
- El Mínimo Común Múltiplo (MCM) de dos o más números es el menor número positivo que es múltiplo común de todos ellos. En otras palabras, es el número más pequeño que se puede dividir por cada uno de los números dados.
- El Máximo Común Divisor (MCD), por su parte, es el mayor número que divide exactamente a todos los números dados. Es útil para simplificar fracciones, resolver ecuaciones y encontrar factores comunes entre números.
En este conjunto de ejercicios resueltos, exploraremos cómo calcular el MCM y el MCD de diferentes conjuntos de números, utilizando distintos métodos. Cada ejercicio será desglosado paso a paso, para que puedas entender claramente las técnicas y estrategias necesarias para resolver problemas relacionados con estos conceptos.
Dos corredores salen al mismo tiempo de la línea de salida de una pista circular. El primer corredor tarda 3 minutos en volver a pasar por la línea de salida y el segundo corredor tarda 4 minutos. ¿Después de cuántos minutos después de haber salido, vuelven a coincidir en la línea de salida?
Tenemos que calcular el 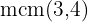
En primer lugar descomponemos los números en factores primos
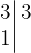
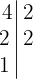
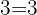
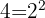
Tomamos los comunes y no comunes de mayor exponente
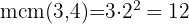
Coinciden nuevamente en la línea de salida 12 minutos después de haber iniciado
Juan trabaja cada 6 días de vigilante en una empresa. Pedro también trabaja de vigilante en la misma empresa cada 8 días. Si ambos coinciden el 1 de febrero, ¿cuándo vuelven a coincidir en la empresa?
Tenemos que calcular el 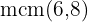
En primer lugar descomponemos los números en factores primos
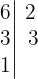
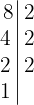
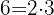
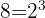
Tomamos los comunes y no comunes de mayor exponente
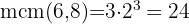
Juan y Pedro coinciden nuevamente en la empresa 24 días después, es decir, el 25 de febrero
María es profesora de un grupo niños. Si compra una bolsa con 36 paletas y otra con 54 caramelos para repartir a sus alumnos de manera que todos tengan la misma cantidad y esta sea la máxima sin sobrar dulces. ¿Cuántos alumnos tiene María?
Tenemos que calcular el 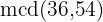
En primer lugar descomponemos los números en factores primos

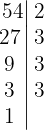
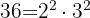
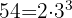
Tomamos los comunes y de menor exponente
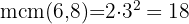
María tiene 18 alumnos
Un faro se enciende cada  segundos, otro cada 18 segundos y un tercero cada minuto. A las
segundos, otro cada 18 segundos y un tercero cada minuto. A las 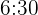 de la tarde los tres coinciden. Averigua las veces que volverán a coincidir en los cinco minutos siguientes.
de la tarde los tres coinciden. Averigua las veces que volverán a coincidir en los cinco minutos siguientes.
Debemos tener todos los tiempos en la misma unidad, por ejemplo en segundos.
El primer faro se enciende en el segundo  , en el
, en el  , en el
, en el  , en el
, en el  , en el
, en el  ... Son los múltiplos de
... Son los múltiplos de 
El segundo faro se enciende en el segundo  , en el
, en el  , en el
, en el  , en el
, en el  , en el
, en el  ... Son los múltiplos de
... Son los múltiplos de 
El tercer faro se enciende en el segundo  , en el
, en el  , en el
, en el 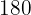 , en el
, en el  , en el
, en el  ... Son los múltiplos de
... Son los múltiplos de 
El segundo en el que los tres faros se encienden es el menor número que puede ser dividido por 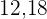 y
y  .
.
Por tanto tenemos que calcular el 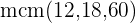
En primer lugar descomponemos los números en factores primos






Tomamos los comunes y no comunes de mayor exponente
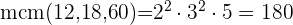
Coinciden por primera vez a los 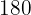 segundos
segundos
 , coinciden cada
, coinciden cada  minutos, por tanto en los
minutos, por tanto en los  minutos siguientes sólo coinciden una vez.
minutos siguientes sólo coinciden una vez.
Solo coinciden a las 6:33 hrs
Un viajero va a Barcelona cada  días y otro cada
días y otro cada  días. Hoy han estado los dos en Barcelona. ¿Dentro de cuantos días volverán a estar los dos a la vez en Barcelona?
días. Hoy han estado los dos en Barcelona. ¿Dentro de cuantos días volverán a estar los dos a la vez en Barcelona?
El primer viajero viaja el día  , el día
, el día  , el día
, el día  , el día
, el día  , el día
, el día  ... Son los múltiplos de
... Son los múltiplos de 
El segundor viajero viaja el día  , el día
, el día  , el día
, el día  , el día
, el día  , el día
, el día  ... Son los múltiplos de
... Son los múltiplos de 
Los dos coinciden cuando viajan el mismo día, es decir, cuando viajan un día que es múltiplo de  y de
y de  . El primer día que coinciden es el menor número que puede ser dividido por
. El primer día que coinciden es el menor número que puede ser dividido por  y
y 
Por tanto tenemos que calcular el 
En primer lugar descomponemos los números en factores primos




Tomamos los comunes y no comunes de mayor exponente
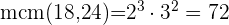
Dentro de 72 días
¿Cuál es el menor número que al dividirlo separadamente por  y
y  , en cada caso, da de resto
, en cada caso, da de resto  ?
?
El menor numero que divide a  y
y  es su m.c.m al que sumaremos
es su m.c.m al que sumaremos  para que al dividir el m.c.m. por cualquiera de los cuatro números dé de resto
para que al dividir el m.c.m. por cualquiera de los cuatro números dé de resto 
En primer lugar descomponemos los números en factores primos








Tomamos los comunes y no comunes de mayor exponente
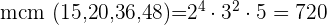
 729
729
En una bodega hay  toneles de vino, cuyas capacidades son:
toneles de vino, cuyas capacidades son: 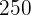 L,
L,  L, y
L, y 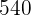 L. Su contenido se quiere envasar en cierto número de garrafas iguales. Calcular las capacidades máximas de estas garrafas para que en ellas se pueden envasar el vino contenido en cada uno de los toneles, y el número de garrafas que se necesitan.
L. Su contenido se quiere envasar en cierto número de garrafas iguales. Calcular las capacidades máximas de estas garrafas para que en ellas se pueden envasar el vino contenido en cada uno de los toneles, y el número de garrafas que se necesitan.
Para poder envasar los 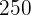 L en garrafas más pequeñas tenemos que elegir un número que sea divisor de
L en garrafas más pequeñas tenemos que elegir un número que sea divisor de 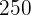
Para poder envasar los  L en garrafas más pequeñas tenemos que elegir un número que sea divisor de
L en garrafas más pequeñas tenemos que elegir un número que sea divisor de 
Para poder envasar los 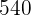 L en garrafas más pequeñas tenemos que elegir un número que sea divisor de
L en garrafas más pequeñas tenemos que elegir un número que sea divisor de 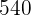
Como el contenido de las garrafas ha de ser el máximo posible, debemos hallar el 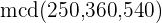
En primer lugar descomponemos los números en factores primos






Tomamos los comunes de menor exponente
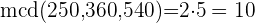
Capacidad de las garrafas  L
L
Número de garrafas de 
Número de garrafas de 
Número de garrafas de 
Número de garrafas  115 garrafas.
115 garrafas.
El suelo de una habitación, que se quiere embaldosar, tiene  m de largo y
m de largo y  m de ancho. Calcula el lado de la baldosa y el número de las baldosas, tal que el número de baldosas que se coloque sea mínimo y que no sea necesario cortar ninguna de ellas.
m de ancho. Calcula el lado de la baldosa y el número de las baldosas, tal que el número de baldosas que se coloque sea mínimo y que no sea necesario cortar ninguna de ellas.
Para que el número de baldosas sea mínimo, las baldosas tiene que tener la máxima superficie
Por tanto tenemos que hallar el máximo común divisor
Como las baldosas se suelen medir en centímetros, pasamos todo a centímetros.



Descomponemos los números en factores primos




Tomamos los comunes de menor exponente
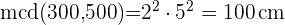 de lado
de lado
Calculamos el área de una baldosa

Calculamos el número de baldosas, dividiendo el área total entre el área de una baldosa
 15 baldosas
15 baldosas
Un comerciante desea poner en cajas  manzanas y
manzanas y  naranjas, de modo que cada caja contenga el mismo número de manzanas o de naranjas y, además, el mayor número posible. Hallar el número de naranjas de cada caja y el número de cajas necesarias.
naranjas, de modo que cada caja contenga el mismo número de manzanas o de naranjas y, además, el mayor número posible. Hallar el número de naranjas de cada caja y el número de cajas necesarias.
Para poner  manzanas en en cajas más pequeñas con el mismo número de manzanas, tenemos que elegir un número que sea divisor de
manzanas en en cajas más pequeñas con el mismo número de manzanas, tenemos que elegir un número que sea divisor de  .
.
Igualmente debemos tener un divisor de  para las naranjas
para las naranjas
Como cada caja debe contener el mayor número de piezas tenemos que hallar el 
Descomponemos los números en factores primos




Tomamos los comunes de menor exponente

 piezas en cada caja.
piezas en cada caja.
Cajas de naranjas 
Cajas de manzanas 
Cajas necesarias  200
200
¿Cuánto mide la mayor baldosa cuadrada que cabe en un número exacto de veces en una sala de  m de longitud y
m de longitud y  de anchura? ¿Y cuántas baldosas se necesitan?
de anchura? ¿Y cuántas baldosas se necesitan?
Por tanto tenemos que hallar el máximo común divisor
Como las baldosas se suelen medir en centímetros, pasamos todo a centímetros.


Área 
Descomponemos los números en factores primos




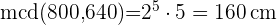 de lado
de lado
Calculamos el área de una baldosa

Calculamos el número de baldosas, dividiendo el área total entre el área de una baldosa
 20 baldosas
20 baldosas
¿Buscas un profe mates?
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)