
Máximo común divisor
El máximo común divisor, 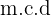 . de dos o más números es el mayor número que divide a todos de manera exacta.
. de dos o más números es el mayor número que divide a todos de manera exacta.
Cálculo del máximo común divisor
1Se descomponen todos los números en factores primos.
2Se toman los factores comunes con menor exponente.
3Se multiplican los factores comunes con menor exponente.
Ejemplo: Hallar el  de:
de: 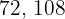 y
y 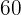 .
.
1Descomponemos los números en factores primos

Así, los números se escriben de la forma

2Los factores comunes con menor exponente son 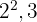
3Para calcular el 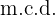 multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente

Hay que notar que si un número es divisor de otro, entonces éste es el 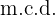 de ambos
de ambos
Ejemplo: El número  es divisor de
es divisor de  , por lo que
, por lo que 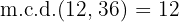
Mínimo común múltiplo
El mínimo común múltiplo  es el menor de todos múltiplos comunes a varios números, excluido el cero.
es el menor de todos múltiplos comunes a varios números, excluido el cero.
Cálculo del mínimo común múltiplo
1Se descomponen los números en factores primos.
2Se toman los factores comunes y no comunes con mayor exponente.
3Se multiplican los factores comunes y no comunes con mayor exponente.
Ejemplo: Hallar el  de:
de: 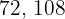 y
y 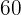 .
.
1Descomponemos los números en factores primos

Así, los números se escriben de la forma

2Los factores comunes y no comunes con mayor exponente son 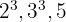
3Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente
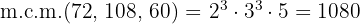
Así,  es el menor número que puede ser dividido por
es el menor número que puede ser dividido por 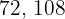 y
y 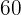 .
.
Hay que notar que si un número es múltiplo de otro, entonces éste es el  de ambos
de ambos
Ejemplo: El número  es múltplo de
es múltplo de  , por lo que
, por lo que 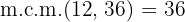
Relación entre el máximo común divisor y el mínimo común múltiplo
Dado que el máximo común divisor y el mínimo común múltiplo están formados por el producto de los factores comunes con menor exponente y el producto de los factores comunes y no comunes con mayor exponente, respectivamente, entonces
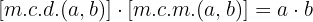
Ejercicios propuestos
Calcular el 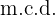 y
y  de
de  y
y 
1Descomponemos los números en factores primos

Así, los números se escriben de la forma

2Los factores comunes con menor exponente son 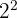
3Para calcular el 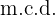 multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente

4Los factores comunes y no comunes con mayor exponente son 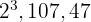
5Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente
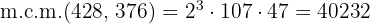
Calcular el 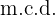 y
y  de
de  y
y 
1Descomponemos los números en factores primos

Así, los números se escriben de la forma

2Los factores comunes con menor exponente son 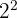
3Para calcular el 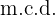 multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente
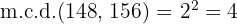
4Los factores comunes y no comunes con mayor exponente son 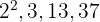
5Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente
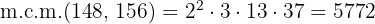
Calcular el 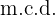 y
y  de
de  y
y 
1Descomponemos los números en factores primos
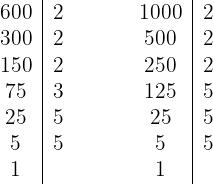
Así, los números se escriben de la forma
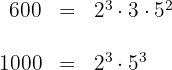
2Los factores comunes con menor exponente son 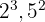
3Para calcular el 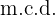 multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente
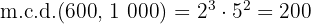
4Los factores comunes y no comunes con mayor exponente son 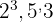
5Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente
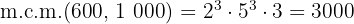
Calcular el 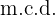 y
y  de
de  y
y 
1Descomponemos los números en factores primos
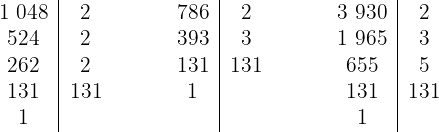
Así, los números se escriben de la forma

2Los factores comunes con menor exponente son 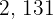
3Para calcular el 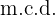 multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente

4Los factores comunes y no comunes con mayor exponente son 
5Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente

Calcular el 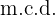 y
y  de
de 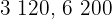 y
y 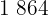
1Descomponemos los números en factores primos
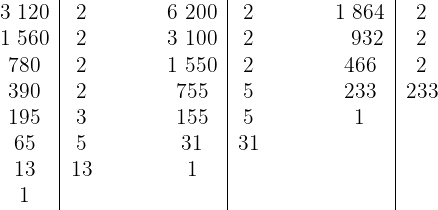
Así, los números se escriben de la forma

2Los factores comunes con menor exponente son 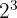
3Para calcular el 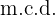 multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente
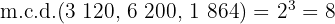
4Los factores comunes y no comunes con mayor exponente son 
5Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente
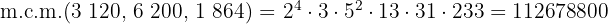
Un faro se enciende cada  segundos, otro cada
segundos, otro cada  segundos y un tercero cada minuto. A las
segundos y un tercero cada minuto. A las 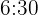 de la tarde los tres coinciden. ¿A qué hora volveran a coincidir nuevamente?
de la tarde los tres coinciden. ¿A qué hora volveran a coincidir nuevamente?
1Descomponemos los números en factores primos
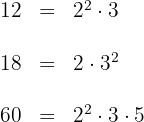
2Calculamos el  de los tres números
de los tres números
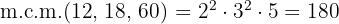
3Los faron coinciden cada 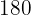 segundos que es lo mismo que
segundos que es lo mismo que  minutos; por lo tanto vuelven a coincidir a las
minutos; por lo tanto vuelven a coincidir a las 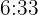 de la tarde
de la tarde
Un viajero va a Barcelona cada  días y otro cada
días y otro cada  días. Hoy han estado los dos en Barcelona. ¿Dentro de cuantos días volverán a estar los dos a la vez en Barcelona?
días. Hoy han estado los dos en Barcelona. ¿Dentro de cuantos días volverán a estar los dos a la vez en Barcelona?
1Descomponemos los números en factores primos
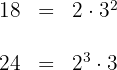
2Calculamos el  de los dos números
de los dos números
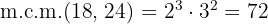
3Los dos viajeros volverán a coincidir dentro de  días.
días.
¿Cuál es el menor número que al dividirlo separadamente por  y
y 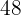 en cada caso da de resto
en cada caso da de resto  ?
?
1Descomponemos los números en factores primos

2Calculamos el  de los cuatro números
de los cuatro números

3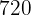 es el menor número que divisible por los cuatro números, así que si deseamos que al dividir por los cuatro números se tenga resto
es el menor número que divisible por los cuatro números, así que si deseamos que al dividir por los cuatro números se tenga resto  , entonces el número debe ser
, entonces el número debe ser 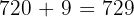 .
.
En una bodega hay  toneles de vino, cuyas capacidades son
toneles de vino, cuyas capacidades son 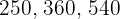 litros respectivamente. Su contenido se quiere envasar en cierto número de garrafas iguales. Calcular las capacidades máximas de estas garrafas para que en ellas se pueden envasar el vino contenido en cada uno de los toneles, y el número de garrafas que se necesitan.
litros respectivamente. Su contenido se quiere envasar en cierto número de garrafas iguales. Calcular las capacidades máximas de estas garrafas para que en ellas se pueden envasar el vino contenido en cada uno de los toneles, y el número de garrafas que se necesitan.
1Descomponemos los números en factores primos
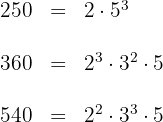
2Calculamos el 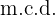 de los tres números
de los tres números
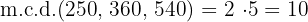
3La capacidad de cada garrafa es de  litros y el número de garrafas es de
litros y el número de garrafas es de  .
.
El suelo de una habitación, que se quiere embaldosar, tiene 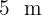 de largo y
de largo y 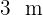 de ancho. Calcula el lado en decímetros y el número de baldosas, tal que el número de baldosas que se coloque sea mínimo y que no sea necesario cortar ninguna de ellas.
de ancho. Calcula el lado en decímetros y el número de baldosas, tal que el número de baldosas que se coloque sea mínimo y que no sea necesario cortar ninguna de ellas.
1El suelo de la habitación a embaldosar tiene medidas  de largo y
de largo y 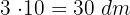 de ancho
de ancho
2Calculamos el 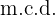 de los dos números
de los dos números
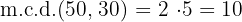
3El lado de cada baldosa es de 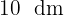 y se requieren
y se requieren  baldosas de largo y
baldosas de largo y  de ancho, por lo que en total se requieren
de ancho, por lo que en total se requieren 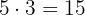 baldosas.
baldosas.
Un comerciante desea poner en cajas 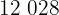 manzanas y
manzanas y 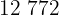 naranjas, de modo que cada caja contenga el mismo número de manzanas o de naranjas y, además, el mayor número posible. Hallar el número de naranjas de cada caja y el número de cajas necesarias.
naranjas, de modo que cada caja contenga el mismo número de manzanas o de naranjas y, además, el mayor número posible. Hallar el número de naranjas de cada caja y el número de cajas necesarias.
1Calculamos el 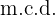

2Calculamos el número de cajas requeridas

Así, el número de cajas requeridas es 
¿Cuánto mide la mayor baldosa cuadrada que cabe en un número exacto de veces en una sala de  de longitud y
de longitud y  de anchura? ¿Y cuántas baldosas se necesitan?
de anchura? ¿Y cuántas baldosas se necesitan?
1El suelo de la habitación a embaldosar tiene medidas  de longitud y
de longitud y  de ancho
de ancho
2Calculamos el 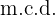 de los dos números
de los dos números
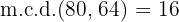
3El lado de cada baldosa es de 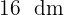 y se requieren
y se requieren 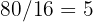 baldosas de largo y
baldosas de largo y 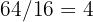 de ancho, por lo que en total se requieren
de ancho, por lo que en total se requieren  baldosas.
baldosas.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)