Elige la opción correcta:
es divisor de 
y de 
, entonces...
Selecciona una respuesta.
Esto debido a que tenemos una propiedad del máximo común divisor que nos dice : Los divisores comunes de varios números coinciden con los divisores del máximo común divisor.
Notemos que
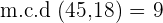
y es divisor de 
.
Sabemos que m.c.d.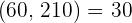 
. Como 
y 
son divisores de 
y de 
, entonces...
Selecciona una respuesta.
Sabemos que si dos números son divisores de otros, su multiplicación también será divisor de los números. Por tanto, y son divisores de y de , entonces 
es divisor de y de .
Por lo tanto, como veíamos en la pregunta anterior, es divisor de 
Sea m.c.d. 
. Observando que 
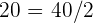y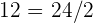 
, podemos afirmar que...
Selecciona una respuesta.
Esto debido a que existe una propiedad que dice lo siguiente: Dados varios números, si se multiplican o dividen por otro número entonces su mcd también queda multiplicado o dividido por el mismo número.
Sabemos que m.c.d.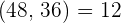 
. Entonces...
Selecciona una respuesta.
Esto se sigue directamente de la propiedad que se menciono en la pregunta anterior.
y 
...
Selecciona una respuesta.
Puesto que para ser primos entre si su único divisor común debe ser 
.
m.c.d.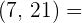 
...
Selecciona una respuesta.
Tenemos que es divisible entre si mismo y además es divisible por también.
m.c.d.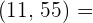 
...
Selecciona una respuesta.
Igual que el ejercicio anterior.
Resuelve los siguientes problemas:
A Eva le encantan las manualidades y esta tarde ha decidido hacer pulseras con su madre. Quiere adornarlas con perlas. Si tiene 
perlas blancas y 
azules, y quiere hacer el máximo número de pulseras posibles de manera que haya la misma cantidad de cada color de perla en cada una de ellas ¿Cuántas pulseras podrá hacer como máximo?
pulseras
Este campo es obligatorio.
El número de pulseras debe ser divisor de y y además debe ser el mayor divisor de ambos, por lo que usamos el mcd.
Descomponemos y en factores primos
Por tanto
Eva podrá hacer 12 pulseras como máximo.
Ampliación: Observemos que cada pulsera estará adornada con 
perlas blancas y 
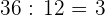perlas azules.
En un laboratorio se están mezclando tres compuestos. Del primero se tienen mg, del segundo 
mg y del tercero 
mg. Se necesita hacer el máximo número de muestras posibles de manera que haya la misma cantidad de cada compuesto en cada una de ellas. ¿Cuántas muestras podremos hacer?
muestras. Indica la cantidad del compuesto del que teníamos 90 mg en cada una de las mezclas.
mg.
Este campo es obligatorio.
Calculamos el máximo común divisor y para esto, descomponemos en factores primos :
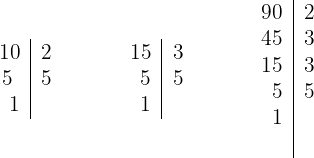
obteniendo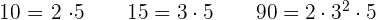 
Es decir, m.c.d
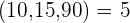y por tanto, se podrán hacer como máximo 5 muestras.
Cada muestra contendrá: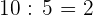 
mg del primer compuesto.
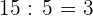mg del segundo compuesto.
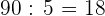mg del último compuesto
En cada una de las mezclas habrá 18 mg del compuesto del que teníamos 90 mg.
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)