Capítulos
- Divisibilidad
- Criterio de divisibilidad por 2
- Criterio de divisibilidad por 3
- Criterio de divisibilidad por 4
- Criterio de divisibilidad por 5
- Criterio de divisibilidad por 6
- Criterio de divisibilidad por 7
- Criterio de divisibilidad por 8
- Criterio de divisibilidad por 9
- Criterio de divisibilidad por 10
- Criterio de divisibilidad por 11
- Criterio de divisibilidad por 25
- Criterio de divisibilidad por 125
Divisibilidad
Un número 
es divisible por otro 
cuándo la división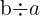 
es exacta, es decir, resulta un número entero.
Ejemplos:
- El número
es divisible por 
porque la división es exacta: 
. - El número también es divisible por
porque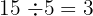 
.
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división. Son muy útiles para
1 Descomponer números en factores
2 Simplificar fracciones
Criterio de divisibilidad por 2
Un número es divisible por 
, si termina en cero o cifra par.
Ejemplos:
Criterio de divisibilidad por 3
Un número es divisible por , si la suma de sus dígitos es múltiplo de .
Ejemplos:
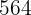
es múltiplo de 
es múltiplo de
Criterio de divisibilidad por 4
Un número es divisible por 
, si sus dos últimas cifras son ceros o múltiplo de .
Ejemplos:
es múltiplo de 
los dos dígitos son ceros
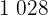
es múltiplo de
Criterio de divisibilidad por 5
Un número es divisible por , si termina en cero o cinco.
Ejemplos:
Criterio de divisibilidad por 6
Un número es divisible por , si es divisible por y por .
Ejemplos:
es múltiplo de , además 
es múltiplo de
Así que es múltiplo de 
es múltiplo de , además 
es múltiplo de
Así que es múltiplo de 
es múltiplo de , además 
es múltiplo de
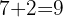
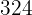
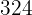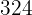
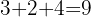
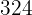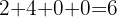
Así que es múltiplo de
Criterio de divisibilidad por 7
Un número es divisible por 
cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 
ó un múltiplo de .
Ejemplos:
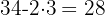
es múltiplo de 
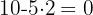
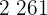
Se repite el proceso con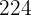 
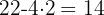
es múltiplo de
Criterio de divisibilidad por 8
Un número es divisible por 
, si sus tres últimas cifras son ceros o múltiplo de .
Ejemp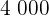los:
los últimos dígitos son ceros
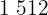
es múltiplo de 
es múltiplo de
Criterio de divisibilidad por 9
Un número es divisible por , si la suma de sus dígitos es múltiplo de .
Ejemplos:
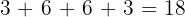
es múltiplo de 
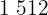
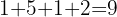
es múltiplo de 
es múltiplo de
Criterio de divisibilidad por 10
Un número es divisible por 
, si la cifra de las unidades es .
Ejemplos:
Criterio de divisibilidad por 11
Un número es divisible por 
, si la diferencia entre la suma de las cifras que ocupan los lugares impares y la de los pares es o un múltiplo de .
Ejemplos:
Criterio de divisibilidad por 25
Un número es divisible por 
, si sus dos últimas cifras son ceros o múltiplo de .
Ejemplos:
Criterio de divisibilidad por 125
Un número es divisible por 
, si sus tres últimas cifras son ceros o múltiplo de .
Ejemplos:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
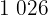
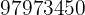
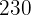
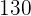
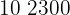
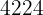
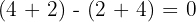
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)