Capítulos
La divisibilidad es un concepto fundamental en matemáticas que nos permite comprender cómo los números se relacionan entre sí. Nos permite determinar si un número es divisible por otro sin necesidad de realizar divisiones exactas.
El Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) son conceptos fundamentales en teoría de números que tienen múltiples aplicaciones en diversos campos de las matemáticas y la resolución de problemas cotidianos. El MCM nos permite encontrar el menor múltiplo común entre dos o más números, mientras que el MCD nos ayuda a identificar el mayor divisor común.
A través de la práctica y la comprensión de las reglas de divisibilidad, podrás desarrollar habilidades para simplificar cálculos, factorizar números y resolver una amplia gama de problemas matemáticos.

Números primos y compuestos
Calcula todos los múltiplos de 17 comprendidos entre 800 y 860.
Primero dividimos 800 entre 17, lo que nos da 47 con 1 de residuo. Esto significa  es menor a 800, pero
es menor a 800, pero  es mayor a 800. Si realizamos la multiplicación nos da
es mayor a 800. Si realizamos la multiplicación nos da
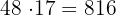
Luego, considerando los enteros siguientes al 48, tenemos
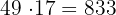

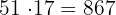
Observemos que 867 ya es mayor a 860. Por lo tanto, el resultado es: 816, 833, 850
Calcula todos los múltiplos de 23 comprendidos entre 500 y 570.
Primero dividimos 500 entre 23, lo que nos da 21 con 17 de residuo. Esto significa 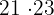 es menor a 500, pero
es menor a 500, pero 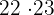 es mayor a 500. Si realizamos la multiplicación nos da
es mayor a 500. Si realizamos la multiplicación nos da
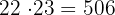
Luego, considerando los enteros siguientes al 22, tenemos
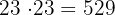
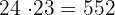
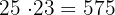
Observemos que 575 ya es mayor a 570. Por lo tanto, el resultado es: 506, 529, 552, 575
Calcula todos los múltiplos de 29 comprendidos entre 700 y 790.
Primero dividimos 700 entre 29, lo que nos da 24 con 4 de residuo. Esto significa  es menor a 700, pero
es menor a 700, pero 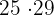 es mayor a 700. Si realizamos la multiplicación nos da
es mayor a 700. Si realizamos la multiplicación nos da
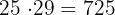
Luego, considerando los enteros siguientes al 25, tenemos
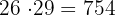
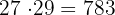
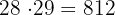
Observemos que 812 ya es mayor a 790. Por lo tanto, el resultado es: 725, 754, 783
De los siguientes números: 179, 311, 848, 3566, 7287, indica cuales son primos y cuales compuestos.
Tenemos que:
Los números 848 y 3566 son compuestos porque, al acabar en cifra par, son divisibles por dos.
El número 7287 también es compuesto porque es divisible entre 3, esto lo sabemos porque la suma de sus digitos es divisible entre 3.
El número 179 es primo porque no es divisible entre 2, 3, 5, 7, 11. Vamos a probar dividiendo por 13:
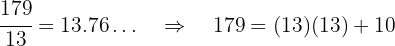
Como la división no es exacta y el cociente es igual al divisor, entonces el número es primo.
El número 311 es primo porque no es divisible entre 2, 3, 5, 7, 11. Probaremos dividiendo por 13:

podemos continuar y vemos que la división no es exacta hasta 311, por lo tanto número primo.
Calcula, mediante una tabla, todos los números primos comprendidos entre 400 y 450.
Debemos construir una tabla como la siguiente. Primero cancelamos todos los números pares, después todos los múltiplos de 3, luego los múltiplos de 5 y así sucesivamente hasta llegar al 19 (el número primo más grande que puede ser factor). Los números que quedan sin tachar son números primo
| 401 | 409 | ||||||||
| 419 | |||||||||
| 421 | |||||||||
| 431 | 433 | 439 | |||||||
| 443 | 449 |
Números primos: 401, 409, 419, 421, 431, 433, 439, 443, 449
Factorización
Factoriza 261 y calcula su número de divisores.
En primer lugar descomponemos en factores:

es decir,
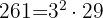
Sumamos la unidad a cada uno de los exponentes de los factores de 261. Luego multiplicamos los resultados obtenidos, entonces,
Número de factores:
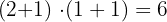
Factoriza 216 y calcula su número de divisores.
En primer lugar descomponemos en factores:

es decir,
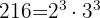
Sumamos la unidad a cada uno de los exponentes de los factores de 216. Luego multiplicamos los resultados obtenidos, entonces,
Número de factores:
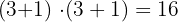
Factoriza 342 y calcula su número de divisores.
En primer lugar descomponemos en factores:

es decir,
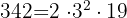
Sumamos la unidad a cada uno de los exponentes de los factores de 342. Luego multiplicamos los resultados obtenidos, entonces,
Número de factores:
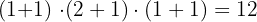
Haz la descomposición en factores de los siguientes números:
-
- 216
-
- 360
-
- 432
216: Hacemos la descomposición en números primos comenzando con el 2, si no se puede 3, luego 5, y así sucesivamente

entonces

2 360:

entonces
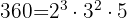
3 432:

entonces
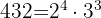
Haz la descomposición de factores de:
-
- 2250
-
- 3500
-
- 2520
2250:Similar a uno de los ejercicios anteriores

por tanto
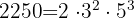
2 3500:

por lo tanto
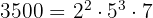
3 2520:

por tanto
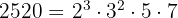
Máximo común divisor, mínimo común múltiplo y algoritmo de Euclides
Calcula el máximo común divisor (m.c.d.) y mínimo común múltiplo (m.c.m.) de:
-
- 30 y 400
-
- 60 y 100
1 30 y 400:
Descomponemos en factores
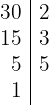
y
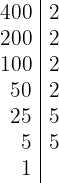
entonces
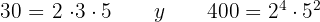
Calculamos m.c.m y m.c.d :
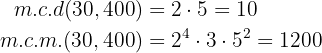
2 60 y 100 : Nuevamente, comenzamos descomponiendo en factores
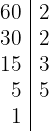
es decir 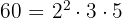 y
y

es decir 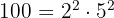 . Ya con los factores obtenemos que el m.c.d es
. Ya con los factores obtenemos que el m.c.d es
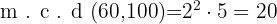
y el m.c.m
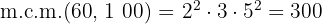
Calcula el máximo común divisor (m.c.d.) y mínimo común múltiplo (m.c.m.) de:
-
- 428 y 376
-
- 148 y 156
1 428 y 376 :En primer lugar descomponemos en factores,

es decir 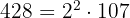 y
y

es decir, 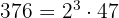 . Para hallar el m.c.d. tomamos los factores comunes de menor exponente
. Para hallar el m.c.d. tomamos los factores comunes de menor exponente
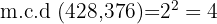
Para hallar el m.c.m. tomamos los factores comunes y no comunes de mayor exponente
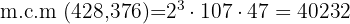
2 148 y 156:
Descomponemos en factores

y
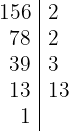
entonces
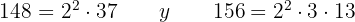
Calculamos m.c.m y m.c.d :
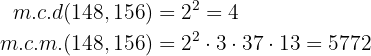
Calcula el máximo común divisor (m.c.d.) y mínimo común múltiplo (m.c.m.) de:
-
- 300 y 500
-
- 600 y 1 000
1 300 y 500:
Descomponemos en factores
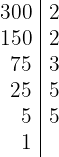
y
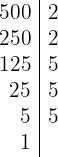
entonces
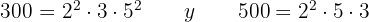
Calculamos m.c.m y m.c.d :
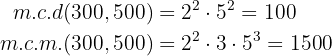
2 600 y 1000 : Nuevamente, comenzamos descomponiendo en factores
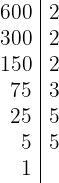
es decir 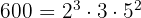 y
y
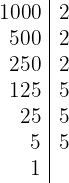
es decir 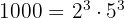 . Ya con los factores obtenemos que el m.c.d es
. Ya con los factores obtenemos que el m.c.d es
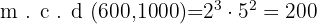
y el m.c.m
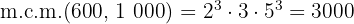
Calcula el m. c. d. y m.c.m. de:
-
- 72, 108 y 60
-
- 1048, 786 y 3930
1 72, 108 y 60:Descomponemos en factores y obtenemos que
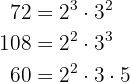
Para hallar el m.c.d. tomamos los factores comunes de menor exponente
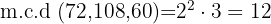
Para hallar el m.c.m. tomamos los factores comunes y no comunes de mayor exponente
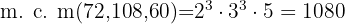
2 1048, 786 y 3930:
Nuevamente descomponemos en factores y obtenemos que
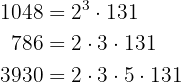
entonces

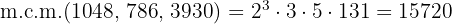
Calcula, utilizando el algoritmo de Euclides, el m.c.d. de:
-
- 72 y 16
-
- 656 y 848
-
- 1278 y 842
1 72 y 16:Primero dividimos el mayor (72) entre el menor (16), si no hay residuo 16 es la maxima medida comun, en este caso obtenemos que

es decir obtenemos un resto de 8, por lo tanto repetimos el proceso y dividimos el divisor(16) entre el residuo(8), y si es exacto, entonces 8 es la maxima medida comun. Notemos que
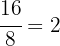
por lo tanto, 8 es el m.c.d.
2 656 y 848:
Repitiendo el proceso anterior, tendremos que la división entre 848 y 656 no es exacta, dividimos el divisor (656) entre el resto obtenido (192).
Puesto que esta división tampoco es exacta tenemos que dividir el divisor (80) entre el resto (32). Pero esta división tampoco es exacta. Ahora dividimos el divisor (32) entre el resto (16)

Como la división es exacta el m.c.d. es el divisor de esta última división: 16.
3 1278 y 842:
Primero dividimos el mayor (1278) entre el menor (842), si no hay residuo 842 es la maxima medida comun, en este caso obtenemos que
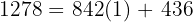
es decir obtenemos un resto de 436, por lo tanto repetimos el proceso y dividimos el divisor(842) entre el residuo(436), obteniendo

es decir obtenemos un resto de 406, por lo tanto repetimos el proceso y dividimos el divisor(436) entre el residuo(406), donde obtenemos un residuo de 30 por lo que es necesario repetir el proceso, esta vez 406 entre el residuo 30 y nuevamente no es exacto, en este caso tenemos que
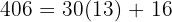
es decir, el residuo es de 16 y hacemos otro vez el proceso con 30 y 16, el cual no es exacto y se obtiene un residuo de 14. Utilizando el divisor 16 y residuo 14 checamos si la division es exacta y comprobamos que obtenemos un residuo de 2, es decir 14 no es el m.c.d, procedemos con el 14 y el 2 de donde
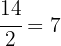
al obtener un resultado exacto se concluye que m.c.d(1278,842) = 2
¿Vives en la capital andaluza? ¡Échales un ojo a nuestras clases particulares matematicas Sevilla!
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)