Las raíces cuadradas son una herramienta fundamental en matemáticas que nos permite encontrar el valor de un número que, al ser multiplicado por sí mismo, produce un resultado igual al número original. Conocer cómo obtener raíces cuadradas paso a paso es crucial para resolver una variedad de problemas en diversas áreas, desde la geometría hasta la física y la ingeniería.
El proceso de obtener una raíz cuadrada puede parecer complejo al principio, pero siguiendo una serie de pasos claros y metodológicos, podemos simplificarlo y hacerlo accesible para todos. A continuación, te guiaré a través de un método paso a paso que te permitirá encontrar raíces cuadradas con confianza y precisión.
Calcula las raíces cuadradas de los siguientes valores:
1264
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra (2) calculamos el número que elevado al cuadrado se aproxime más por defecto
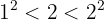
por tanto tomamos 1 y lo colocamos en la casilla, será la 1ª cifra de la raíz
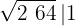
3El cuadrado del número obtenido se resta a la primera cifra
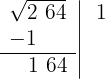
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (64), separamos del número formado, la primera cifra a la derecha (4) y dividimos lo que resta (16) entre el doble del número que tenemos en la casilla, es decir entre 2 · 1=2
Debajo de la casilla colocamos otra con el doble obtenido (2) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
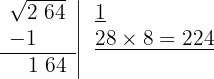
5 Como este número es superior al resto (164), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
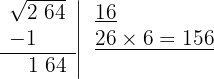
6 Restamos el producto obtenido (156) al resto (164)
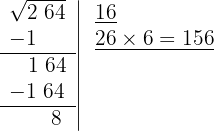
7 Significa que 16 es la raíz y 8 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 264, es decir 16² y determina la cantidad necesaria para llegar a la cifra en cuestión 8.
8 Comprobamos el resultado haciendo la prueba:
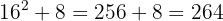
2351
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra calculamos el número que elevado al cuadrado se aproxime más por defecto

por tanto tomamos 1 y lo colocamos en la casilla, será la 1ª cifra de la raíz
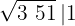
3El cuadrado del número obtenido se resta a la primera cifra
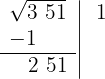
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (51), separamos del número formado, la primera cifra a la derecha (1) y dividimos lo que resta (25) entre el doble del número que tenemos en la casilla, es decir entre 2 · 1=2
El cociente de la división es mayor que 10, por lo que escogemos el 9 y debajo de la casilla colocamos otra con el doble obtenido (2) seguido del cociente de la división que al ser mayor que 10 elegimos (9) y el número formado se multiplica por el cociente obtenido (9)
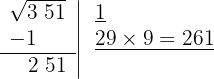
5 Como este número es superior al resto (251), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 8 el resultado obtenido es menor que el resto, por tanto colocamos 8 como segunda cifra de la raíz
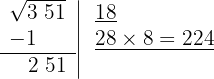
6 Restamos el producto obtenido (224) al resto (251)
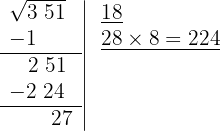
7 Significa que 18 es la raíz y 27 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 351, es decir 18² y determina la cantidad necesaria para llegar a la cifra en cuestión 27.
8 Comprobamos el resultado haciendo la prueba:
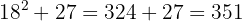
3721
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra (2) calculamos el número que elevado al cuadrado se aproxime más por defecto
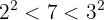
por tanto tomamos 2 y lo colocamos en la casilla, será la 1ª cifra de la raíz
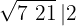
3El cuadrado del número obtenido se resta a la primera cifra
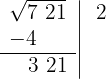
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (21), separamos del número formado, la primera cifra a la derecha (1) y dividimos lo que resta (32) entre el doble del número que tenemos en la casilla, es decir entre 2 · 2=4
Debajo de la casilla colocamos otra con el doble obtenido (4) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
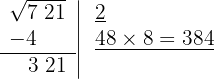
5 Como este número es superior al resto (321), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
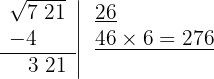
6 Restamos el producto obtenido (276) al resto (321)
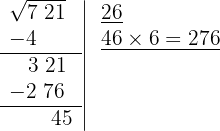
7 Significa que 26 es la raíz y 45 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 721, es decir 26² y determina la cantidad necesaria para llegar a la cifra en cuestión 45.
8 Comprobamos el resultado haciendo la prueba:
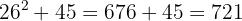
4999
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra (2) calculamos el número que elevado al cuadrado se aproxime más por defecto
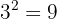
por tanto tomamos 3 y lo colocamos en la casilla, será la 1ª cifra de la raíz
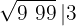
3El cuadrado del número obtenido se resta a la primera cifra
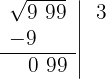
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (99), separamos del número formado, la primera cifra a la derecha (9) y dividimos lo que resta (9) entre el doble del número que tenemos en la casilla, es decir entre 2 · 3=6
Debajo de la casilla colocamos otra con el doble obtenido (6) seguido del cociente de la división (1) y el número formado se multiplica por el cociente obtenido (1)
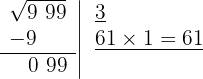
5 Como este número es inferior al resto (99), por tanto colocamos 1 como segunda cifra de la raíz
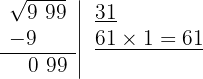
6 Restamos el producto obtenido (61) al resto (99)
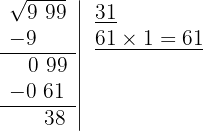
7 Significa que 31 es la raíz y 38 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 999, es decir 31² y determina la cantidad necesaria para llegar a la cifra en cuestión 38.
8 Comprobamos el resultado haciendo la prueba:

56256
1Separamos las cifras en grupos de dos, empezando por la derecha
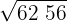
2Con la primera cifra (62) calculamos el número que elevado al cuadrado se aproxime más por defecto
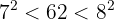
por tanto tomamos 7 y lo colocamos en la casilla, será la 1ª cifra de la raíz
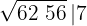
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (56), separamos del número formado, la primera cifra a la derecha (6) y dividimos lo que resta (135) entre el doble del número que tenemos en la casilla, es decir entre 2 · 7=14
El cociente de la división es 9 y debajo de la casilla colocamos otra con el doble obtenido (14) seguido del cociente de la división (9) y el número formado se multiplica por el cociente obtenido (9)
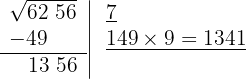
5 Como este número es inferior al resto (1356), colocamos 9 como segunda cifra de la raíz
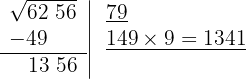
6 Restamos el producto obtenido (1341) al resto (1356)
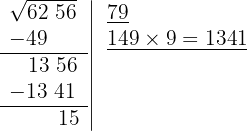
7 Significa que 79 es la raíz y 15 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 6256, es decir 79² y determina la cantidad necesaria para llegar a la cifra en cuestión 15.
8 Comprobamos el resultado haciendo la prueba:

68900
1Separamos las cifras en grupos de dos, empezando por la derecha
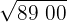
2Con la primera cifra (89) calculamos el número que elevado al cuadrado se aproxime más por defecto

por tanto tomamos 9 y lo colocamos en la casilla, será la 1ª cifra de la raíz
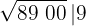
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (00), separamos del número formado, la primera cifra a la derecha (0) y dividimos lo que resta (80) entre el doble del número que tenemos en la casilla, es decir entre 2 · 9=18
El cociente de la división es 4 y debajo de la casilla colocamos otra con el doble obtenido (18) seguido del cociente de la división (4) y el número formado se multiplica por el cociente obtenido (4)
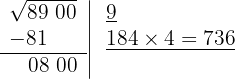
5 Como este número es inferior al resto (800), colocamos 4 como segunda cifra de la raíz
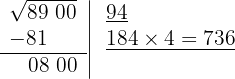
6 Restamos el producto obtenido (736) al resto (800)
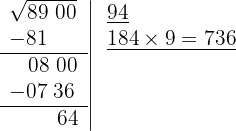
7 Significa que 94 es la raíz y 64 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 8900, es decir 94² y determina la cantidad necesaria para llegar a la cifra en cuestión 64.
8 Comprobamos el resultado haciendo la prueba:

772675
1Separamos las cifras en grupos de dos, empezando por la derecha
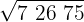
2Con la primera cifra (7) calculamos el número que elevado al cuadrado se aproxime más por defecto
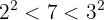
por tanto tomamos 2 y lo colocamos en la casilla, será la 1ª cifra de la raíz

3El cuadrado del número obtenido se resta a la primera cifra
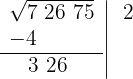
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (26), separamos del número formado, la primera cifra a la derecha (6) y dividimos lo que resta (32) entre el doble del número que tenemos en la casilla, es decir entre 2 · 2=4
El cociente de la división es 8 y debajo de la casilla colocamos otra con el doble obtenido (4) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
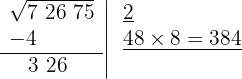
5 Como este número es superior al resto (326), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
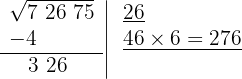
6 Restamos el producto obtenido (276) al resto (326)
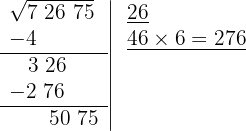
7 >Detrás del resto colocamos el siguiente grupo cifras del radicando (75), separando del número formado la primera cifra a la derecha (5) y dividimos lo que resta (507) entre el doble del número que tenemos en la casilla, es decir entre 2 · 26=52
El cociente de la división es 9 y debajo de la casilla colocamos otra con el doble obtenido (52) seguido del cociente de la división (9) y el número formado se multiplica por el cociente obtenido (9)
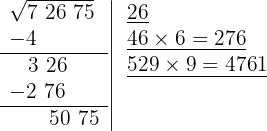
8 Como este número es inferior al resto (5075), colocamos 9 como tercera cifra de la raíz
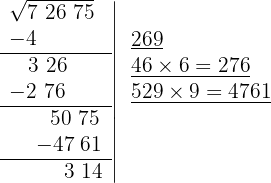
9 Significa que 269 es la raíz y 314 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 72675, es decir 269² y determina la cantidad necesaria para llegar a la cifra en cuestión 314.
10 Comprobamos el resultado haciendo la prueba:
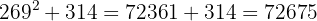
899875
1Separamos las cifras en grupos de dos, empezando por la derecha
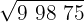
2Con la primera cifra (9) calculamos el número que elevado al cuadrado se aproxime más por defecto
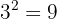
por tanto tomamos 3 y lo colocamos en la casilla, será la 1ª cifra de la raíz
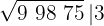
3El cuadrado del número obtenido se resta a la primera cifra
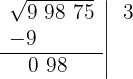
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (98), separamos del número formado, la primera cifra a la derecha (8) y dividimos lo que resta (9) entre el doble del número que tenemos en la casilla, es decir entre 2 · 3=6
El cociente de la división es 1 y debajo de la casilla colocamos otra con el doble obtenido (6) seguido del cociente de la división (1) y el número formado se multiplica por el cociente obtenido (1)
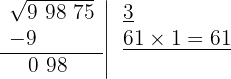
5 Como este número es inferior al resto (98), colocamos 1 como segunda cifra de la raíz
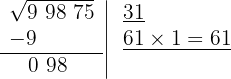
6 Restamos el producto obtenido (61) al resto (98)
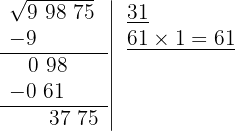
7 >Detrás del resto colocamos el siguiente grupo cifras del radicando (75), separando del número formado la primera cifra a la derecha (5) y dividimos lo que resta (377) entre el doble del número que tenemos en la casilla, es decir entre 2 · 31=62
El cociente de la división es 6 y debajo de la casilla colocamos otra con el doble obtenido (62) seguido del cociente de la división (6) y el número formado se multiplica por el cociente obtenido (6)
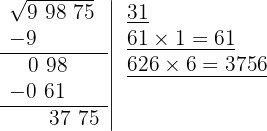
8 Como este número es inferior al resto (3775), colocamos 6 como tercera cifra de la raíz
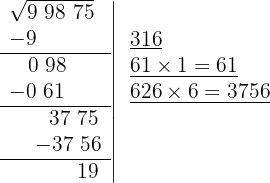
9 Significa que 316 es la raíz y 19 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 99875, es decir 316² y determina la cantidad necesaria para llegar a la cifra en cuestión 19.
10 Comprobamos el resultado haciendo la prueba:
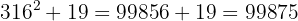
9264.315
1Separamos las cifras en grupos de dos, empezando por la derecha de manera que los decimales queden en grupos de dos
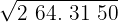
2Con la primera cifra (9) calculamos el número que elevado al cuadrado se aproxime más por defecto

por tanto tomamos 1 y lo colocamos en la casilla, será la 1ª cifra de la raíz

3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (64), separamos del número formado, la primera cifra a la derecha (4) y dividimos lo que resta (16) entre el doble del número que tenemos en la casilla, es decir entre 2 · 1=2
El cociente de la división es 8 y debajo de la casilla colocamos otra con el doble obtenido (2) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
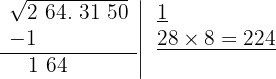
5 Como este número es superior al resto (164), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
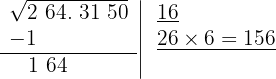
6 Restamos el producto obtenido (156) al resto (164)

7 >Detrás del resto colocamos el siguiente grupo cifras del radicando (31), separando del número formado la primera cifra a la derecha (1) y dividimos lo que resta (83) entre el doble del número que tenemos en la casilla, es decir entre 2 · 16=32
El cociente de la división es 2 y debajo de la casilla colocamos otra con el doble obtenido (32) seguido del cociente de la división (2) y el número formado se multiplica por el cociente obtenido (2)
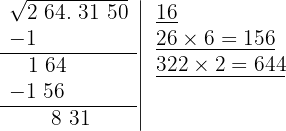
8 Como este número es inferior al resto (831), colocamos 2 como tercera cifra de la raíz anteponiendole un punto, ya que la cifra 31 pertenece a los decimales
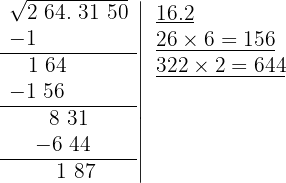
9 >Detrás del resto colocamos el siguiente grupo cifras del radicando (50), separando del número formado la primera cifra a la derecha (0) y dividimos lo que resta (1875) entre el doble del número que tenemos en la casilla sin el punto decimal, es decir entre 2 · 162=324
El cociente de la división es 5 y debajo de la casilla colocamos otra con el doble obtenido (324) seguido del cociente de la división (5) y el número formado se multiplica por el cociente obtenido (5)
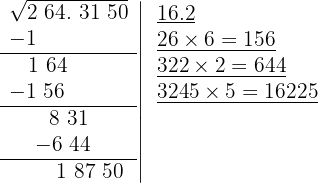
10 Como este número es inferior al resto (18750), colocamos 5 como cuarta cifra de la raíz
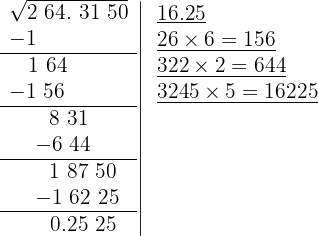
11 Significa que 16.25 es la raíz y 0.2525 es el resto.
1072675.687
Siguiendo los pasos de los ejercicios anteriores se tiene

Significa que 269.58 es la raíz y 2.3106 es el resto.
Calcula las raíces cuadradas de los siguientes valores:
264
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra (2) calculamos el número que elevado al cuadrado se aproxime más por defecto
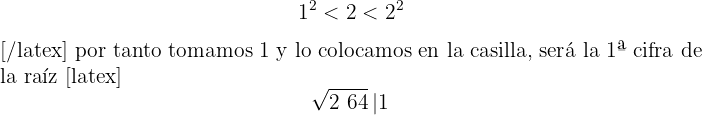
3El cuadrado del número obtenido se resta a la primera cifra
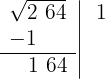
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (64), separamos del número formado, la primera cifra a la derecha (4) y dividimos lo que resta (16) entre el doble del número que tenemos en la casilla, es decir entre 2 · 1=2
Debajo de la casilla colocamos otra con el doble obtenido (2) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
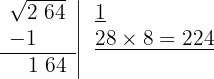
5 Como este número es superior al resto (164), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
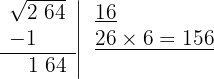
6 Restamos el producto obtenido (156) al resto (164)
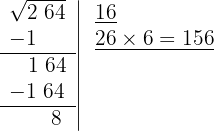
7 Significa que 16 es la raíz y 8 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 264, es decir 16² y determina la cantidad necesaria para llegar a la cifra en cuestión 8.
8 Comprobamos el resultado haciendo la prueba:
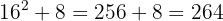
351
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra calculamos el número que elevado al cuadrado se aproxime más por defecto
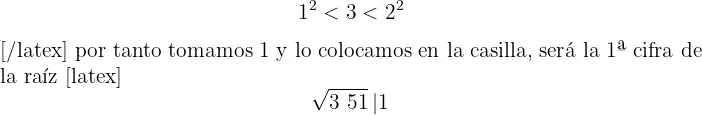
3El cuadrado del número obtenido se resta a la primera cifra
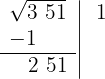
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (51), separamos del número formado, la primera cifra a la derecha (1) y dividimos lo que resta (25) entre el doble del número que tenemos en la casilla, es decir entre 2 · 1=2
El cociente de la división es mayor que 10, por lo que escogemos el 9 y debajo de la casilla colocamos otra con el doble obtenido (2) seguido del cociente de la división que al ser mayor que 10 elegimos (9) y el número formado se multiplica por el cociente obtenido (9)
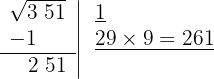
5 Como este número es superior al resto (251), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 8 el resultado obtenido es menor que el resto, por tanto colocamos 8 como segunda cifra de la raíz
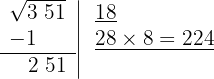
6 Restamos el producto obtenido (224) al resto (251)
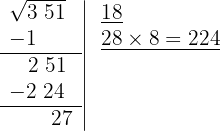
7 Significa que 18 es la raíz y 27 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 351, es decir 18² y determina la cantidad necesaria para llegar a la cifra en cuestión 27.
8 Comprobamos el resultado haciendo la prueba:
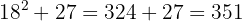
721
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra (2) calculamos el número que elevado al cuadrado se aproxime más por defecto
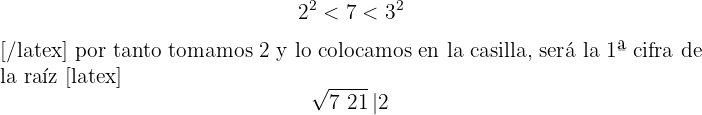
3El cuadrado del número obtenido se resta a la primera cifra
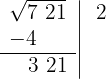
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (21), separamos del número formado, la primera cifra a la derecha (1) y dividimos lo que resta (32) entre el doble del número que tenemos en la casilla, es decir entre 2 · 2=4
Debajo de la casilla colocamos otra con el doble obtenido (4) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
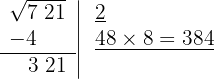
5 Como este número es superior al resto (321), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
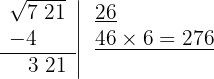
6 Restamos el producto obtenido (276) al resto (321)
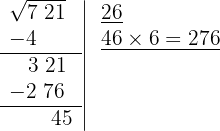
7 Significa que 26 es la raíz y 45 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 721, es decir 26² y determina la cantidad necesaria para llegar a la cifra en cuestión 45.
8 Comprobamos el resultado haciendo la prueba:
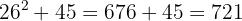
999
1Separamos las cifras en grupos de dos, empezando por la derecha

2Con la primera cifra (2) calculamos el número que elevado al cuadrado se aproxime más por defecto
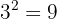
por tanto tomamos 3 y lo colocamos en la casilla, será la 1ª cifra de la raíz
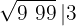
3El cuadrado del número obtenido se resta a la primera cifra
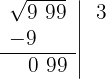
4 Detrás del resto colocamos el siguiente grupo cifras del radicando (99), separamos del número formado, la primera cifra a la derecha (9) y dividimos lo que resta (9) entre el doble del número que tenemos en la casilla, es decir entre 2 · 3=6
Debajo de la casilla colocamos otra con el doble obtenido (6) seguido del cociente de la división (1) y el número formado se multiplica por el cociente obtenido (1)
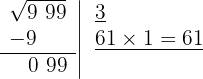
5 Como este número es inferior al resto (99), por tanto colocamos 1 como segunda cifra de la raíz
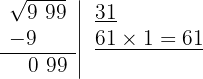
6 Restamos el producto obtenido (61) al resto (99)
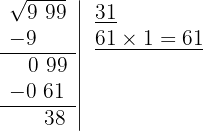
7 Significa que 31 es la raíz y 38 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 999, es decir 31² y determina la cantidad necesaria para llegar a la cifra en cuestión 38.
8 Comprobamos el resultado haciendo la prueba:

6256
1Separamos las cifras en grupos de dos, empezando por la derecha
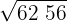
2Con la primera cifra (62) calculamos el número que elevado al cuadrado se aproxime más por defecto
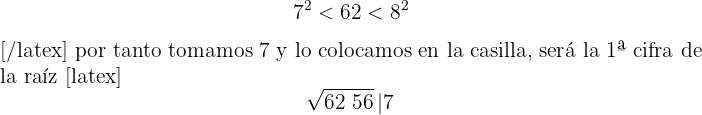
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (56), separamos del número formado, la primera cifra a la derecha (6) y dividimos lo que resta (135) entre el doble del número que tenemos en la casilla, es decir entre 2 · 7=14
El cociente de la división es 9 y debajo de la casilla colocamos otra con el doble obtenido (14) seguido del cociente de la división (9) y el número formado se multiplica por el cociente obtenido (9)
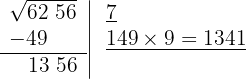
5 Como este número es inferior al resto (1356), colocamos 9 como segunda cifra de la raíz
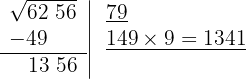
6 Restamos el producto obtenido (1341) al resto (1356)
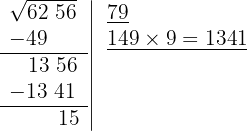
7 Significa que 79 es la raíz y 15 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 6256, es decir 79² y determina la cantidad necesaria para llegar a la cifra en cuestión 15.
8 Comprobamos el resultado haciendo la prueba:

8900
1Separamos las cifras en grupos de dos, empezando por la derecha
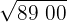
2Con la primera cifra (89) calculamos el número que elevado al cuadrado se aproxime más por defecto
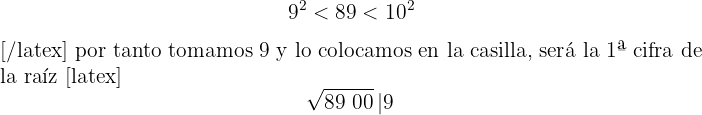
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (00), separamos del número formado, la primera cifra a la derecha (0) y dividimos lo que resta (80) entre el doble del número que tenemos en la casilla, es decir entre 2 · 9=18
El cociente de la división es 4 y debajo de la casilla colocamos otra con el doble obtenido (18) seguido del cociente de la división (4) y el número formado se multiplica por el cociente obtenido (4)
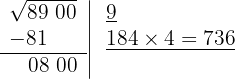
5 Como este número es inferior al resto (800), colocamos 4 como segunda cifra de la raíz
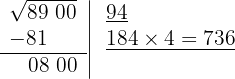
6 Restamos el producto obtenido (736) al resto (800)
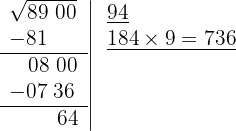
7 Significa que 94 es la raíz y 64 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 8900, es decir 94² y determina la cantidad necesaria para llegar a la cifra en cuestión 64.
8 Comprobamos el resultado haciendo la prueba:

72675
1Separamos las cifras en grupos de dos, empezando por la derecha
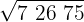
2Con la primera cifra (7) calculamos el número que elevado al cuadrado se aproxime más por defecto
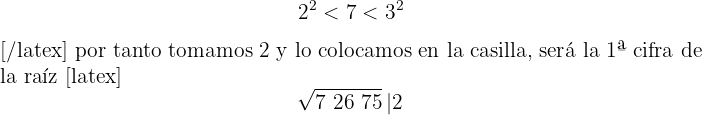
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (26), separamos del número formado, la primera cifra a la derecha (6) y dividimos lo que resta (32) entre el doble del número que tenemos en la casilla, es decir entre 2 · 2=4
El cociente de la división es 8 y debajo de la casilla colocamos otra con el doble obtenido (4) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
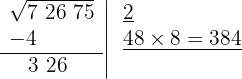
5 Como este número es superior al resto (326), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
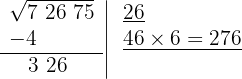
6 Restamos el producto obtenido (276) al resto (326)
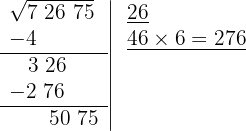
7 >Detrás del resto colocamos el siguiente grupo cifras del radicando (75), separando del número formado la primera cifra a la derecha (5) y dividimos lo que resta (507) entre el doble del número que tenemos en la casilla, es decir entre 2 · 26=52
El cociente de la división es 9 y debajo de la casilla colocamos otra con el doble obtenido (52) seguido del cociente de la división (9) y el número formado se multiplica por el cociente obtenido (9)
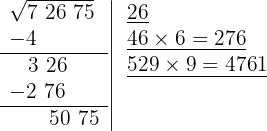
8 Como este número es inferior al resto (5075), colocamos 9 como tercera cifra de la raíz
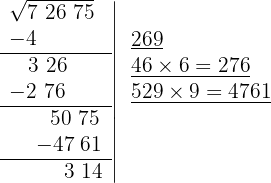
9 Significa que 269 es la raíz y 314 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 72675, es decir 269² y determina la cantidad necesaria para llegar a la cifra en cuestión 314.
10 Comprobamos el resultado haciendo la prueba:
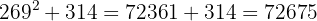
99875
1Separamos las cifras en grupos de dos, empezando por la derecha
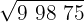
2Con la primera cifra (9) calculamos el número que elevado al cuadrado se aproxime más por defecto
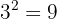
por tanto tomamos 3 y lo colocamos en la casilla, será la 1ª cifra de la raíz
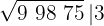
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (98), separamos del número formado, la primera cifra a la derecha (8) y dividimos lo que resta (9) entre el doble del número que tenemos en la casilla, es decir entre 2 · 3=6
El cociente de la división es 1 y debajo de la casilla colocamos otra con el doble obtenido (6) seguido del cociente de la división (1) y el número formado se multiplica por el cociente obtenido (1)
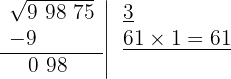
5 Como este número es inferior al resto (98), colocamos 1 como segunda cifra de la raíz
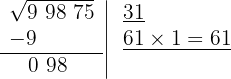
6 Restamos el producto obtenido (61) al resto (98)
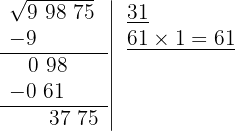
7 >Detrás del resto colocamos el siguiente grupo cifras del radicando (75), separando del número formado la primera cifra a la derecha (5) y dividimos lo que resta (377) entre el doble del número que tenemos en la casilla, es decir entre 2 · 31=62
El cociente de la división es 6 y debajo de la casilla colocamos otra con el doble obtenido (62) seguido del cociente de la división (6) y el número formado se multiplica por el cociente obtenido (6)
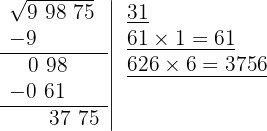
8 Como este número es inferior al resto (3775), colocamos 6 como tercera cifra de la raíz
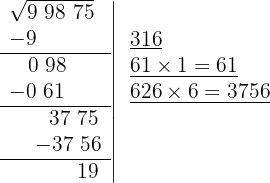
9 Significa que 316 es la raíz y 19 es el resto. El proceso brinda soluciones enteras, significa que encuentra al cuadrado más cercano por la izquierda a la cifra 99875, es decir 316² y determina la cantidad necesaria para llegar a la cifra en cuestión 19.
10 Comprobamos el resultado haciendo la prueba:
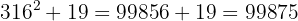
264.315
1Separamos las cifras en grupos de dos, empezando por la derecha de manera que los decimales queden en grupos de dos
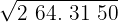
2Con la primera cifra (9) calculamos el número que elevado al cuadrado se aproxime más por defecto
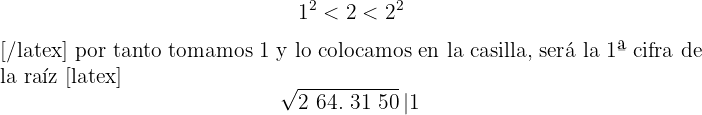
3El cuadrado del número obtenido se resta a la primera cifra

4 Detrás del resto colocamos el siguiente grupo cifras del radicando (64), separamos del número formado, la primera cifra a la derecha (4) y dividimos lo que resta (16) entre el doble del número que tenemos en la casilla, es decir entre 2 · 1=2
El cociente de la división es 8 y debajo de la casilla colocamos otra con el doble obtenido (2) seguido del cociente de la división (8) y el número formado se multiplica por el cociente obtenido (8)
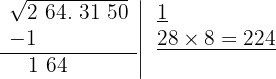
5 Como este número es superior al resto (164), tenemos que ir probando con números menores hasta que el producto sea menor al resto. Con 6 el resultado obtenido es menor que el resto, por tanto colocamos 6 como segunda cifra de la raíz
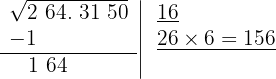
6 Restamos el producto obtenido (156) al resto (164)

7 >Detrás del resto colocamos el siguiente grupo cifras del radicando (31), separando del número formado la primera cifra a la derecha (1) y dividimos lo que resta (83) entre el doble del número que tenemos en la casilla, es decir entre 2 · 16=32
El cociente de la división es 2 y debajo de la casilla colocamos otra con el doble obtenido (32) seguido del cociente de la división (2) y el número formado se multiplica por el cociente obtenido (2)
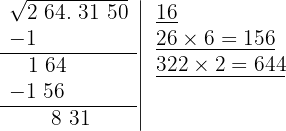
8 Como este número es inferior al resto (831), colocamos 2 como tercera cifra de la raíz anteponiendole un punto, ya que la cifra 31 pertenece a los decimales
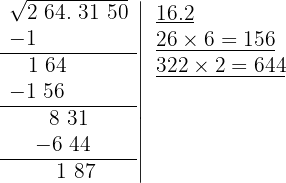
9 >Detrás del resto colocamos el siguiente grupo cifras del radicando (50), separando del número formado la primera cifra a la derecha (0) y dividimos lo que resta (1875) entre el doble del número que tenemos en la casilla sin el punto decimal, es decir entre 2 · 162=324
El cociente de la división es 5 y debajo de la casilla colocamos otra con el doble obtenido (324) seguido del cociente de la división (5) y el número formado se multiplica por el cociente obtenido (5)
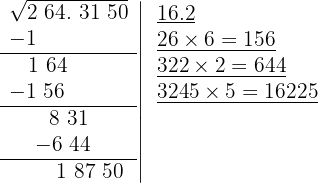
10 Como este número es inferior al resto (18750), colocamos 5 como cuarta cifra de la raíz
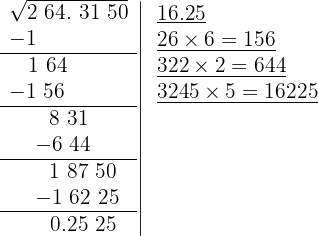
11 Significa que 16.25 es la raíz y 0.2525 es el resto.
72675.687
Siguiendo los pasos de los ejercicios anteriores se tiene

Significa que 269.58 es la raíz y 2.3106 es el resto.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola, revisé mi respuesta y veo que aunque la forma en que escribí la expresión es diferente, el resultado es exactamente el mismo: -138. Ambas expresiones son matemáticamente equivalentes:
Mi respuesta: 19 * -6 + 7 * 6 + 3 * 6 – 14 * 6
Respuesta marcada como correcta: -6 * 19 + 6 * 7 + 6 * 3 – 6 * 14
Ambas siguen las reglas de los signos y la propiedad conmutativa de la multiplicación. Me gustaría saber si hubo algún error en la evaluación automática, ya que el resultado es correcto. Gracias.
Hola el ejercicio que me muestras es correcto y si, tu sigues las reglas entonces el resultado es el mismo, no te equivocaste. ¿Este ejercicio esta en un artículo o es por tu cuenta? Para que si hay un error podamos corregirlo.
He dado a las opciones que habían pero cuando les doy, se quita la opción que he dado anteriormente de forma automática creo que es un fallo o tienen un número límite de respuestas
Es verdad, tiene que ser un fallo por que a mi también me pasa.
se me quitó el resultado en la antepenúltimo ejercicio, pero al momento de corregirlo se me ha puesto como bien.
Hola, podrías decirnos si te pasa con todos los ejercicios o con uno en especifico, para hacer una revisión del artículo y rectificar los errores, te lo agradeceríamos mucho.
Estoy mirando los pasos a resolver una raíz cuadrada y en el paso número 7 está el número 589 que no sé de dónde sale, me podéis decir?
Hola revise los ejercicios y no encontré el ejercicio que mencionas, podrías por favor indicarme el número de ejercicio y con gusto resuelvo tu duda.