Resuelve los siguientes ejercicios de potencias. La casilla de la izquierda representa la base y la casilla de la derecha representa el exponente
1
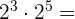
Este campo es obligatorio.
Solución
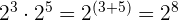
2

Este campo es obligatorio.
Solución
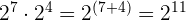
3
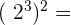
Este campo es obligatorio.
Solución
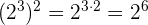
4
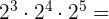
Este campo es obligatorio.
Solución

5
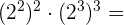
Este campo es obligatorio.
Solución
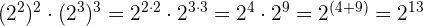
6
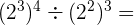
Este campo es obligatorio.
Solución

7
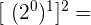
Este campo es obligatorio.
Solución

8

Este campo es obligatorio.
Solución
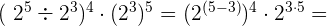

9

Este campo es obligatorio.
Solución

10

Este campo es obligatorio.
Solución
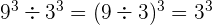
Si tienes dudas puedes consultar las fórmulas de potencias
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me parece interesante cómo los números pueden tener diferentes funciones según el contexto. Los ordinales nos ayudan a entender el orden, mientras que los cardinales indican cantidad. También es curioso que algunos números solo sirvan como identificadores, sin expresar ni posición ni cantidad
Hola, revisé mi respuesta y veo que aunque la forma en que escribí la expresión es diferente, el resultado es exactamente el mismo: -138. Ambas expresiones son matemáticamente equivalentes:
Mi respuesta: 19 * -6 + 7 * 6 + 3 * 6 – 14 * 6
Respuesta marcada como correcta: -6 * 19 + 6 * 7 + 6 * 3 – 6 * 14
Ambas siguen las reglas de los signos y la propiedad conmutativa de la multiplicación. Me gustaría saber si hubo algún error en la evaluación automática, ya que el resultado es correcto. Gracias.
Hola el ejercicio que me muestras es correcto y si, tu sigues las reglas entonces el resultado es el mismo, no te equivocaste. ¿Este ejercicio esta en un artículo o es por tu cuenta? Para que si hay un error podamos corregirlo.
He dado a las opciones que habían pero cuando les doy, se quita la opción que he dado anteriormente de forma automática creo que es un fallo o tienen un número límite de respuestas
Es verdad, tiene que ser un fallo por que a mi también me pasa.
se me quitó el resultado en la antepenúltimo ejercicio, pero al momento de corregirlo se me ha puesto como bien.
Hola, podrías decirnos si te pasa con todos los ejercicios o con uno en especifico, para hacer una revisión del artículo y rectificar los errores, te lo agradeceríamos mucho.
Estoy mirando los pasos a resolver una raíz cuadrada y en el paso número 7 está el número 589 que no sé de dónde sale, me podéis decir?
Hola revise los ejercicios y no encontré el ejercicio que mencionas, podrías por favor indicarme el número de ejercicio y con gusto resuelvo tu duda.