Capítulos

Definición de números naturales
El conjunto de los números naturales está formado por:

Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
Los números naturales están ordenados, lo que nos permite comparar dos números naturales:
 ; 5 es mayor que 3.
; 5 es mayor que 3.
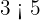 ; 3 es menor que 5.
; 3 es menor que 5.
Los números naturales son ilimitados, si a un número natural le sumamos 1, obtenemos otro número natural.
Suma de números naturales
a + b = c
Los términos de la suma, a y b, se llaman sumandos y el resultado, c, suma.
Propiedades de la suma
1 Interna:

La suma pertenece a los números Naturales
2 Asociativa:
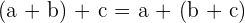
La suma de dos primeros números más un tercero es lo mismo a la suma de un primero más la suma de los dos últimos
Ejemplo
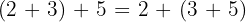
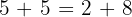
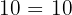
3 Conmutativa:
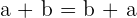
El orden de la suma no altera el resultado
Ejemplo

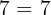
4 Elemento neutro:
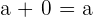
El elemento neutro de la suma te regresa el mismo número en este caso es el cero.
Ejemplo
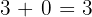
a - b = c
Los términos que intervienen en una resta se llaman: a, minuendo y b, sustraendo. Al resultado, c, lo llamamos diferencia.
Propiedades de la resta
1No es una operación interna
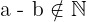
La resta no pertenece a los números Naturales, ya que el resultado podría ser un número negativo.
Ejemplo
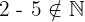
2No es Conmutativa
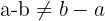
El orden en como realizamos la resta, si altera el resultado
Ejemplo
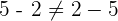
Multiplicación de números naturales
a · b = c
Los términos a y b se llaman factores y el resultado, c, producto.
Propiedades de la multiplicación
1 Interna:

El producto pertenece a los números Naturales
2Asociativa:

Realizar la multiplicación de los dos primero y luego un tercero es igual a realizar la multiplicación de un primero y luego los dos últimos
Ejemplo
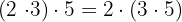
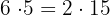
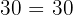
3Conmutativa:
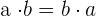
El orden en como realizamos la multiplicación no altera el resultado
Ejemplo

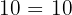
4Elemento neutro:
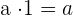
El elemento neutro de la multiplicación es el 1, ya que es quién nos regresa el valor inicial
Ejemplo

5Distributiva:

La multiplicación de un número por una suma se distribuye, es decir, el número lo multiplicamos por cada elemento de la suma
Ejemplo
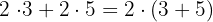
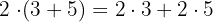
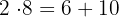

6Sacar factor común:

Si en los elementos de la suma hay término en común, éste se puede factorizar.
Ejemplo
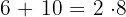

División de números naturales
D : d = c
Los términos que intervienen en un división se llaman, D, dividendo y d divisor. Al resultado, c, lo llamamos cociente.
Propiedades de la división
1División exacta
La división es exacta si al realizar la operación el residuo es cero.
Ejemplo
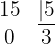

2División entera
La división es entera si al realizar la operación hay un residuo
Ejemplo

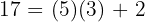
3No es una operación interna

La división no pertenece a los números Naturales, ya que podríamos obtener números decimales.
Ejemplo

4No es Conmutativo:

El orden de la operación sí altera el resultado.
Ejemplo

5Cero dividido entre cualquier número da cero.

Ejemplo
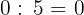
6No se puede dividir por 0.
Propiedades de las potencias
1 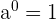
Cualquier número elevado a la cero es uno.
2 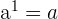
Cualquier número elevado a la 1 es el mismo número.
3 Producto de potencias con la misma base:
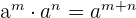
El producto de mismas bases, suma los exponentes.
Ejemplo

4 Cociente de potencias con la misma base:
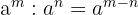
El cociente de mismas bases, resta los exponentes.
Ejemplo

5 Potencia de una potencia:

Potencia de potencia, multiplica los exponentes.
Ejemplo

6 Producto de potencias con el mismo exponente:
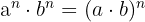
El producto de diferentes bases pero cada uno con el mismo exponente, es igual al producto de las bases elevado al exponente.
Ejemplo
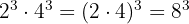
7 Cociente de potencias con el mismo exponente:
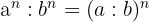
El cociente de diferentes bases pero cada uno con el mismo exponente, es igual al cociente de las bases elevado al exponente.
Ejemplo
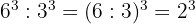
Ejercicios de potencias
1 
2 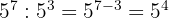
3 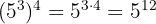
4 
5 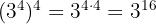
6 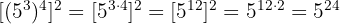
7 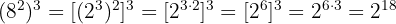
8 
9 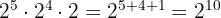
10 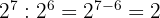
11 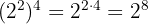
12 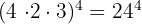
13 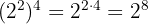
14 
15 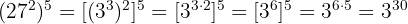
16 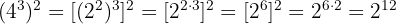
Propiedades de las raíces
1 Raíz exacta: Radicando= 
La raíz exacta es cuando podemos encontrar un número que al multiplicarlo por si mismo nos regrese el radicando.
Ejemplo
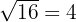

2 Raíz entera: <Radicando= (Raíz)2 + Resto
La raíz entera es cuando podemos encontrar un número que al multiplicarlo por si mismo más un entero nos regrese el radicando.
Ejemplo
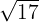

Jerarquía en las operaciones
1 Efectuar las operaciones entre paréntesis, corchetes y llaves.
2 Calcular las potencias y raíces.
3 Efectuar los productos y cocientes.
4 Realizar las sumas y restas.
Operaciones combinadas sin paréntesis
1.1Combinación de sumas y diferencias.
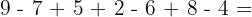
Comenzando por la izquierda, vamos efectuando las operaciones según aparecen.
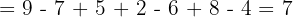
1.2 Combinación de sumas, restas y productos.

Realizamos primero los productos por tener mayor prioridad.

Efectuamos las sumas y restas.
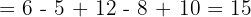
1.3 Combinación de sumas, restas , productos y divisiones.

Realizamos los productos y cocientes en el orden en el que los encontramos porque las dos operaciones tienen la misma prioridad.
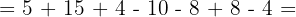
Efectuamos las sumas y restas.
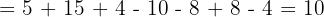
1.4 Combinación de sumas, restas , productos , divisiones y potencias.
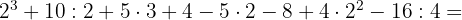
Realizamos en primer lugar las potencias por tener mayor prioridad.
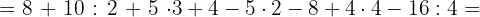
Seguimos con los productos y cocientes.

Efectuamos las sumas y restas.

Operaciones combinadas con paréntesis
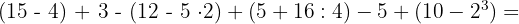
Realizamos en primer lugar las operaciones contenidas en los paréntesis.
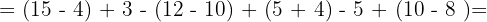
Quitamos paréntesis realizando las operaciones correspondientes.

Operaciones combinadas con paréntesis y corchetes
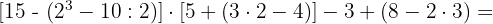
Primero operamos con las potencias, productos y cocientes de los paréntesis.

Realizamos las sumas y restas de los paréntesis.

En vez de poner corchetes pondremos paréntesis directamente:

Operamos en los corchetes.

Multiplicamos.

Restamos y sumamos.
= 83
Ejercicios y problemas resueltos de números naturales
1 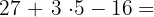
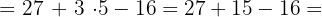 26
26
2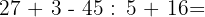
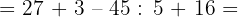 37
37
3 
 40
40
4 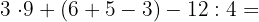
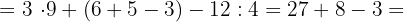 32
32
5 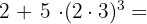
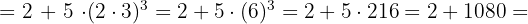 1082
1082
6 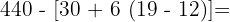
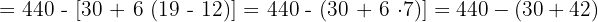
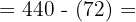 368
368
7 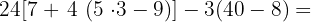
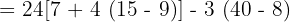
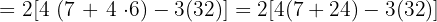
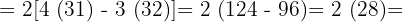 56
56
8 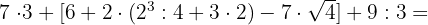
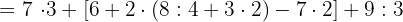
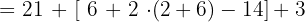
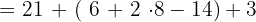

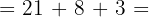 32
32
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola, revisé mi respuesta y veo que aunque la forma en que escribí la expresión es diferente, el resultado es exactamente el mismo: -138. Ambas expresiones son matemáticamente equivalentes:
Mi respuesta: 19 * -6 + 7 * 6 + 3 * 6 – 14 * 6
Respuesta marcada como correcta: -6 * 19 + 6 * 7 + 6 * 3 – 6 * 14
Ambas siguen las reglas de los signos y la propiedad conmutativa de la multiplicación. Me gustaría saber si hubo algún error en la evaluación automática, ya que el resultado es correcto. Gracias.
Hola el ejercicio que me muestras es correcto y si, tu sigues las reglas entonces el resultado es el mismo, no te equivocaste. ¿Este ejercicio esta en un artículo o es por tu cuenta? Para que si hay un error podamos corregirlo.
He dado a las opciones que habían pero cuando les doy, se quita la opción que he dado anteriormente de forma automática creo que es un fallo o tienen un número límite de respuestas
Es verdad, tiene que ser un fallo por que a mi también me pasa.
se me quitó el resultado en la antepenúltimo ejercicio, pero al momento de corregirlo se me ha puesto como bien.
Hola, podrías decirnos si te pasa con todos los ejercicios o con uno en especifico, para hacer una revisión del artículo y rectificar los errores, te lo agradeceríamos mucho.
Estoy mirando los pasos a resolver una raíz cuadrada y en el paso número 7 está el número 589 que no sé de dónde sale, me podéis decir?
Hola revise los ejercicios y no encontré el ejercicio que mencionas, podrías por favor indicarme el número de ejercicio y con gusto resuelvo tu duda.