Capítulos

¿Qué hay que tener en cuenta en la división de los números enteros?
Existen varias cosas que se deben tener presentes cuando se dividen dos números enteros, aquí abordaremos las más importantes, esperando que en adelante sea más familiar su manejo para futuras aplicaciones.
En términos generales debemos saber el signo del resultado y el tipo de número que se tiene al dividirlos, además de otras propiedades.
Veamos lo que pasa con el signo.
El signo que se genera al dividir dos enteros o en general la división de dos números, sigue las mismas propiedades que la multiplicación, ya que una división se puede ver como una multiplicación entre dos valores

1 Si tanto dividendo como divisor tienen el mismo signo, el resultado queda positivo, por ejemplo:
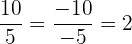
2 Si tanto dividendo como divisor tienen el signo contrario, el resultado queda negativo, por ejemplo:
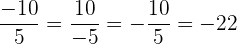
De manera general podemos decir que el signo que se tiene al dividir dos números, es el que se obtiene de la aplicación de la regla de los signos:

Ejemplo:
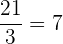
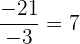
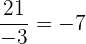

Propiedades de la división de números enteros
1 Una de las propiedades más importantes de la división de números enteros, es que el resultado a veces sale del conjunto de los enteros  , y se generan elementos racionales
, y se generan elementos racionales 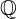 , a esta propuedad se le conoce como no cerradura en
, a esta propuedad se le conoce como no cerradura en  bajo división.
bajo división.
Por ejemplo, si realizamos la siguiente división de enteros, observemos que el resultado ya no es un entero
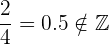
2Una características que tiene la división de enteros es que no es conmutativa, es decir, intercambiar al dividendo y al divisor entre ellos, se genera un nuevo número. Recordemos que la propiedad de conmutatividad se refiere a que no importa el orden en que se pongan los números el resultado es siempre el mismo.
Por ejemplo, si intercambiamos al dividendo con el divisor, no queda el mismo resultado

es decir
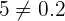
3Cuando uno de los enteros es el cero debemos tener cuidado ya que se puede generar alguna indeterminación, veamos los tres casos
- Si el numerador vale cero y el denominador es distinto de cero, entonces el resultado es cero
- Si el numerador es distinto de cero y el denominador es cero, entonces la fracción no esta definida, no existe
- Si tanto el numerador como el denominador son cero, entonces la fracción está indeterminada
4Cuando la división de dos enteros resulta otro entero, es decir que la división es exacta, significa que el numerador es igual al denominador por el cociente
Si 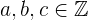 , y la división no es exacta entonces
, y la división no es exacta entonces
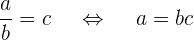
5Cuando la división de dos enteros no es exacta significa que el numerador es igual a el cociente por el denominador mas el residuo
Si 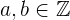 y
y  entonces
entonces
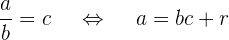
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El ejercicio 15 está mal
Hola revise el ejercicio 15 y habla sobre el recorrido de un barco y no encontré el error, podrías hacernos el favor de mencionar donde está mal, nos ayudaría mucho.
muy buen material de estudio pero se repiten los ejercicios y como ya se las respuestas entonces no estudio nada
Hola te agradecemos tus comentarios, vamos a tomarlos en cuenta para poder mejorar en el contenido y sea de mas provecho.
me gustaría mas ejercicio de operaciones combinadas y así practicar y aprender mas de la matemática que casi un 80 % de los estudiante le huyen
Hola agradecemos tus comentarios, vamos a tomar en cuenta tu recomendación para mejorar en nuestra calidad de artículos y sea mas beneficioso.
Hola , excelente material de estudio, por favor verificar las respuestas de los ejercicios 6 y 7 de los polinomios propuestos , al parecer hay un error en las respuestas. Con todo respeto. gracias
Hola podrías decirme cual es el tema pues el artículo al que me manda es de «Problemas de números enteros con signo» y tu mencionas polinomios, además de que los ejercicios 6 y 7 del tema mencionado están bien.
Hola nuestro deseo es poder contestar todas sus dudas, en este caso para lograrlo necesitamos mas detalles, como por ejemplo si se relaciona con un ejercicio o donde lo viste para si hay un error poder rectificarlo, te lo agradeceríamos mucho.