Realiza los siguientes ejercicios con potencias:
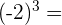
Este campo es obligatorio.
Reescribimos a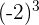 
como
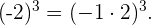
Luego,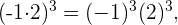 
pero 
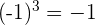y 
.
Así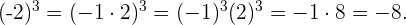 
Este campo es obligatorio.
Reescribimos a 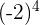como 
Luego,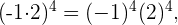 
pero 
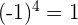y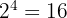 
.
Así
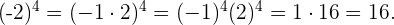
Este campo es obligatorio.
Tenemos un producto de potencias distintas pero con la misma base, entonces se deja la base igual y se suman los exponentes, esto es,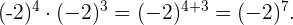 
Ahora reescribimos a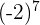 
como 
Luego,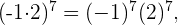
pero 
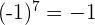y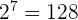 
.
Así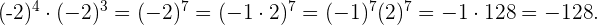 
Este campo es obligatorio.
Tenemos una división de potencias distintas pero con la misma base, entonces se deja la base igual y se restan los exponentes, es decir, 
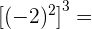
Este campo es obligatorio.
Tenemos una potencia elevada a otra potencia, entonces dejamos la base igual y la elevamos al producto de las potencias:
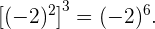
Como en los ejercicios anteriores 
Así, 
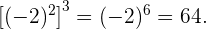
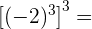
Este campo es obligatorio.
Siguiendo el mismo procedimiento como en el ejercicio anterior tenemos que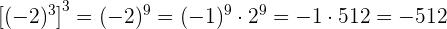 
Este campo es obligatorio.
Sabemos que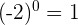 
.
Ahora, dado que tenemos un producto de una misma base elevada a distintas pontencias, dejamos la base y sumamos las potenicas.
Así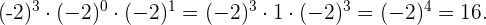 
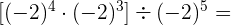
Este campo es obligatorio.
Siguiendo el procedimiento del segundo ejercicio, dejamos la base igual y sumamos las potencias en el corchete:
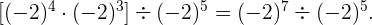
Luego, siguiendo el cuarto ejercicio, dejamos la base y restamos potencias:
Finalmente, 
y así 
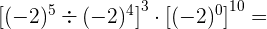
Este campo es obligatorio.
Resolvemos primero la división de potenicas dentro del primer corchete:
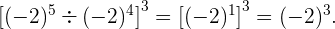
Sabemos que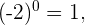 
luego 
Por lo tanto 
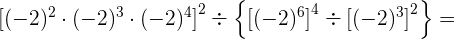
Este campo es obligatorio.
Resolvemos primero las operaciones que están dentro del primer corchete y de la llave:
Así
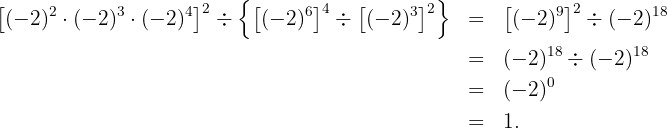
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
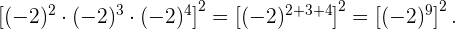
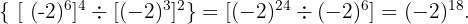
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
muy buen material de estudio pero se repiten los ejercicios y como ya se las respuestas entonces no estudio nada
Hola te agradecemos tus comentarios, vamos a tomarlos en cuenta para poder mejorar en el contenido y sea de mas provecho.
me gustaría mas ejercicio de operaciones combinadas y así practicar y aprender mas de la matemática que casi un 80 % de los estudiante le huyen
Hola agradecemos tus comentarios, vamos a tomar en cuenta tu recomendación para mejorar en nuestra calidad de artículos y sea mas beneficioso.
Hola , excelente material de estudio, por favor verificar las respuestas de los ejercicios 6 y 7 de los polinomios propuestos , al parecer hay un error en las respuestas. Con todo respeto. gracias
Hola podrías decirme cual es el tema pues el artículo al que me manda es de «Problemas de números enteros con signo» y tu mencionas polinomios, además de que los ejercicios 6 y 7 del tema mencionado están bien.
Hola nuestro deseo es poder contestar todas sus dudas, en este caso para lograrlo necesitamos mas detalles, como por ejemplo si se relaciona con un ejercicio o donde lo viste para si hay un error poder rectificarlo, te lo agradeceríamos mucho.