La unidad fundamental para medir el tiempo es el segundo el cual se denota por 
En los ejercicios de medidas de tiempo se utilizan las siguientes equivalencias:
1 
2 
3 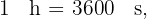

Ejercicios de horas, minutos y segundos
Convertir a horas, minutos y segundos las siguientes expresiones:
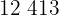 segundos
segundos
1 Al tratarse de segundos, descomponemos el total en término de  para obtener minutos y segundos
para obtener minutos y segundos
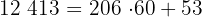
Como 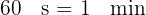 , tenemos
, tenemos
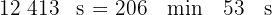
2 Convertimos los 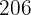 minutos en horas y minutos
minutos en horas y minutos
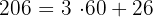
Como  , tenemos
, tenemos
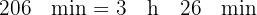
3 De esta forma


1 Al tratarse de segundos, descomponemos el total en término de  para obtener minutos y segundos
para obtener minutos y segundos
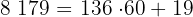
Como  , tenemos
, tenemos
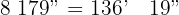
2 Convertimos los  minutos en horas y minutos
minutos en horas y minutos
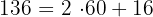
Como 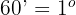 , tenemos
, tenemos

3 De esta forma
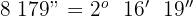
 segundos
segundos
1 Al tratarse de segundos, descomponemos el total en término de  para obtener minutos y segundos
para obtener minutos y segundos
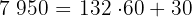
Como 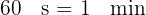 , tenemos
, tenemos
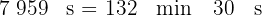
2 Convertimos los  minutos en horas y minutos
minutos en horas y minutos
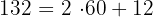
Como  , tenemos
, tenemos
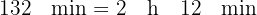
3 De esta forma

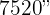
1 Al tratarse de segundos, descomponemos el total en término de  para obtener minutos y segundos
para obtener minutos y segundos

Como  , tenemos
, tenemos

2 Convertimos los  minutos en horas y minutos
minutos en horas y minutos
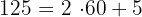
Como 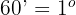 , tenemos
, tenemos
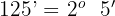
3 De esta forma

 horas
horas
1 Al tratarse de horas, descomponemos el total en término entero y decimal

Como  , tenemos
, tenemos

2 Convertimos los  minutos en minutos y segundos
minutos en minutos y segundos
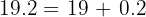
Como  , tenemos
, tenemos

3 De esta forma

Ejercicios de segundos
Expresa en segundos:
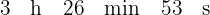
1 Convertimos las horas y minutos en segundos, para esto multiplicamos por  y
y  respectivamente
respectivamente

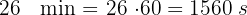
2 Sumamos todos los segundos
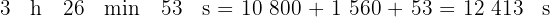
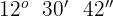
1 Convertimos los grados y minutos en segundos, para esto multiplicamos por  y
y  respectivamente
respectivamente
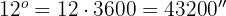
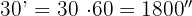
2 Sumamos todos los segundos

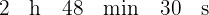
1 Convertimos las horas y minutos en segundos, para esto multiplicamos por  y
y  respectivamente
respectivamente
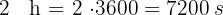

2 Sumamos todos los segundos
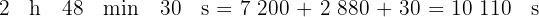

1 Convertimos las horas y minutos en segundos, para esto multiplicamos por  y
y  respectivamente
respectivamente


2 Sumamos todos los segundos
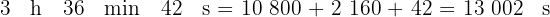
Ejercicio de diferencia
Calcula la siguiente diferencia:
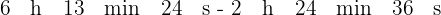
1 Representamos la diferencia

2 Como 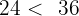 , vamos a tomar un minuto de los
, vamos a tomar un minuto de los  , dejando el total de minutos a
, dejando el total de minutos a  y transformarlo en segundos. Realizamos la resta
y transformarlo en segundos. Realizamos la resta

3 Procedemos de la misma forma con los minutos. Como 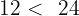 , vamos a tomar una hora de las
, vamos a tomar una hora de las  , dejando el total de horas a
, dejando el total de horas a  y transformarlo en minutos. Realizamos la resta
y transformarlo en minutos. Realizamos la resta

Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Tengo éste problemas como puedo solucionar
Se cambiará el piso de tres habitaciones de una casa los cuales miden 12m2 9m2 u 14m2. Si usan piezas de cerámica de625cm2 ¿ cuántas piezas corresponden a la superficie del piso por cambiar?
Esta mal la imagen.
Hacia abajo se divide y hacia arriba se multiplica
Hola te agradecemos tus comentarios, podrías hacernos el favor de darnos mas detalles, como si la imagen esta en un ejercicio y cual es el número del ejercicio.
muy bueno pero muy largo y cuando te corrige no se alcanza a leer, esta muy chica la letra
Hola agradecemos tus comentarios, en cuanto a lo largo es para ser mas explícitos y en cuanto a la letra pequeña estamos trabajando en ello.
yo quisiera que en la pagina se pudiera resolver los ejercicios
Hola podría ser buena idea la que propones, podrias darnos mas detalles al respecto y posiblemente en un futuro poder cumplir con esta sugerencia tuya.
Hola, cómo se resolvería la resta en el sistema sexagesimal si el minuendo, en grados, es menor que el sustraendo? La profesora dice debe pedir prestado un giro que es igual a 360° y de esa manera resolver.
Hola respondiendo a tu pregunta imagina que a 36 grados y 27 minutos le restas 76 grados y 30 minutos, simplemente harías la resta al revés y al resultado le pones signo negativo en este caso serian menos 40 grados y 3 minutos.
25,56 dam+ 526,9 dm. Lo tengo que llevar todo a metro qué resultado daría?