¡Bienvenidos a nuestra página de ejercicios sobre el sistema métrico decimal! Este sistema de medición es fundamental en el mundo de las matemáticas y la ciencia, y es utilizado universalmente para expresar magnitudes como longitud, masa, volumen, y más.
El sistema métrico decimal, basado en múltiplos de 10, es un método intuitivo y coherente para comprender y convertir unidades de medida. Desde el milímetro hasta el kilómetro, el gramo hasta la tonelada, o el mililitro hasta el litro, este sistema facilita el cálculo y la comparación de medidas, proporcionando una base sólida para la resolución de problemas prácticos en diversas disciplinas.
En esta página, encontrarás una serie de ejercicios diseñados para ayudarte a familiarizarte con el sistema métrico decimal. Aprenderás a convertir entre diferentes unidades de medida, a entender la relación entre ellas y a aplicar estos conceptos a problemas reales. Ya sea que estés comprando comida, construyendo un proyecto o realizando experimentos científicos, el dominio del sistema métrico decimal es una habilidad invaluable.
¡Adelante, empieza a explorar y a dominar el sistema métrico decimal!
Si quieres probar las clases matematicas online, ¡hazlo con Superprof!
Pasa a decímetros cuadrados:
1 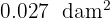
2 
3 
4 
Para pasar a decímetros cuadrados tenemos que:
Multiplicar si es una unidad mayor que el decímetro cuadrado 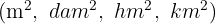 , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el decímetro cuadrado  , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
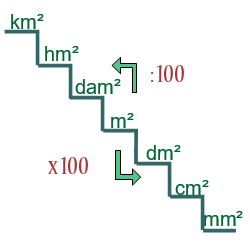
Soluciones:
1 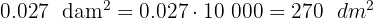
2 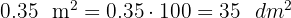
3 
4 
Expresa en metros cuadrados:
1 
2 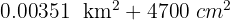
3 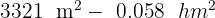
Para pasar a metros cuadrados tenemos que:
Multiplicar si es una unidad mayor que el metro cuadrado  , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el metro cuadrado  , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.

Soluciones:
1 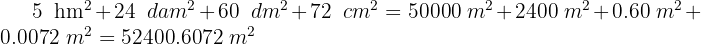
2 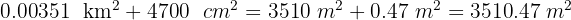
3 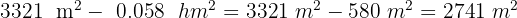
Expresa en hectáreas:
1 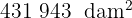
2 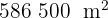
3 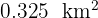
4 
5 
Una hectárea equivale a un hectómetro cuadrado.
Para pasar a hectáreas o a hectómetros cuadrados tenemos que:
Multiplicar si es una unidad mayor que el hectómetro cuadrado 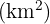 por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el hectómetro cuadrado  por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.

Soluciones:
1 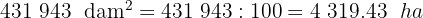
2 
3 
4 
5 
Calcula y expresa el resultado en forma compleja:
1 
2 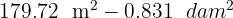
3 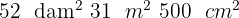
Debemos tener en cuenta que un área equivale a un decámetro cuadrado y una hectárea a un hectómetro cuadrado.

Soluciones:
1 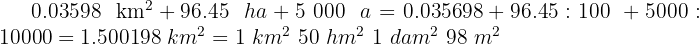
2 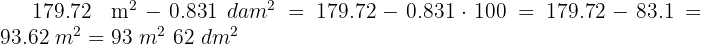
3 
Pasa a centímetros cúbicos:
1 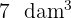
2 
3 
Para pasar a centímetros cúbicos tenemos que:
Multiplicar si es una unidad mayor que el centímetro cúbico 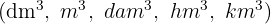 por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el centímetro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.

Soluciones:
1 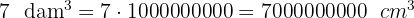
2 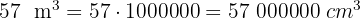
3 
Expresa en metros cúbicos:
1 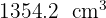
2 
3 
Para pasar a metros cúbicos tenemos que:
Multiplicar si es una unidad mayor que el metro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el metro cúbico 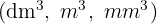 por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.

Soluciones:
1 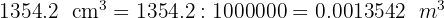
2 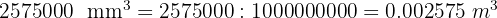
3 
Calcula y expresa el resultado en decímetros cúbicos:

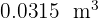
Para pasar a decímetros cúbicos tenemos que:
Multiplicar si es una unidad mayor que el decímetro cúbico 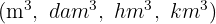 por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el decímetro cúbico 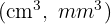 por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.

Soluciones:
1 
2 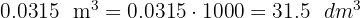
Pasa a decámetros cuadrados:
1 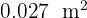
2 
3 
4 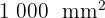
Para pasar a decámetros cuadrados tenemos que:
Multiplicar si es una unidad mayor que el decámetro cuadrado 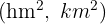 , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el decámetro cuadrado 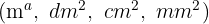 , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.

Soluciones:
1 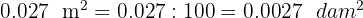
2 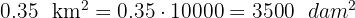
3 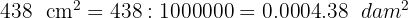
4 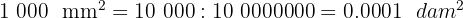
Expresa en hectómetros cuadrados:
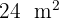

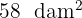
Para pasar a hectómetros cuadrados tenemos que:
Multiplicar si es una unidad mayor que el hectómetro cuadrado  , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el hectómetro cuadrado  , por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
, por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.

Soluciones:
1 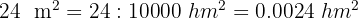
2 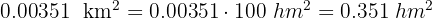
3 
Expresa en kilómetros cuadrados:
1 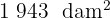
2 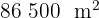
3 
4 
Para pasar a kilómetros cuadrados tenemos que:
Dividir si es una unidad menor que el kilómetro cuadrado 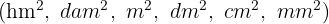 por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.
por la unidad seguida de tantos pares de ceros como lugares haya entre ellas.

Soluciones:
1 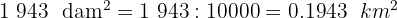
2 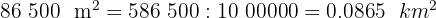
3 
4 
Calcula y expresa el resultado en forma compleja:
1 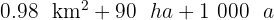
2 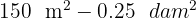
3 
Debemos tener en cuenta que un área equivale a un decámetro cuadrado y una hectárea a un hectómetro cuadrado.

Soluciones:
1 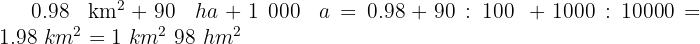
2 
3 
Pasa a metros cúbicos:
1 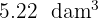
2 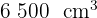
3 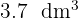
4 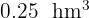
Para pasar a metros cúbicos tenemos que:
Multiplicar si es una unidad mayor que el metro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el metro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.

Soluciones:
1 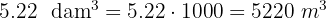
2 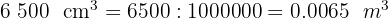
3 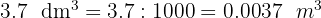
4 
Expresa en centímetros cúbicos:
1 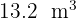
2 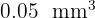
3 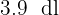
4 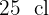
Para pasar a centímetros cúbicos tenemos que:
Multiplicar si es una unidad mayor que el centímetro cúbico 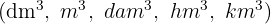 por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el centímetro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.

También tendremos en cuenta que 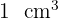 equivale a una capacidad de un
equivale a una capacidad de un  .
.
Soluciones:
1 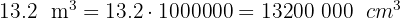
2 
3 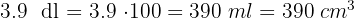
4 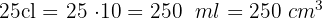
Calcula y expresa el resultado en metros cúbicos:
1 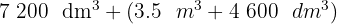
2 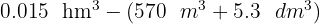
Para pasar a metros cúbicos tenemos que:
Multiplicar si es una unidad mayor que el metro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
Dividir si es una unidad menor que el metro cúbico  por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.

Soluciones:
1 
2 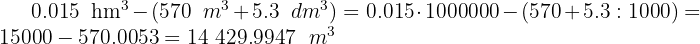
¿Buscas un maestro de matematicas? ¡Encuéntralo en Superprof!
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Tengo éste problemas como puedo solucionar
Se cambiará el piso de tres habitaciones de una casa los cuales miden 12m2 9m2 u 14m2. Si usan piezas de cerámica de625cm2 ¿ cuántas piezas corresponden a la superficie del piso por cambiar?
Esta mal la imagen.
Hacia abajo se divide y hacia arriba se multiplica
Hola te agradecemos tus comentarios, podrías hacernos el favor de darnos mas detalles, como si la imagen esta en un ejercicio y cual es el número del ejercicio.
muy bueno pero muy largo y cuando te corrige no se alcanza a leer, esta muy chica la letra
Hola agradecemos tus comentarios, en cuanto a lo largo es para ser mas explícitos y en cuanto a la letra pequeña estamos trabajando en ello.
yo quisiera que en la pagina se pudiera resolver los ejercicios
Hola podría ser buena idea la que propones, podrias darnos mas detalles al respecto y posiblemente en un futuro poder cumplir con esta sugerencia tuya.
Hola, cómo se resolvería la resta en el sistema sexagesimal si el minuendo, en grados, es menor que el sustraendo? La profesora dice debe pedir prestado un giro que es igual a 360° y de esa manera resolver.
Hola respondiendo a tu pregunta imagina que a 36 grados y 27 minutos le restas 76 grados y 30 minutos, simplemente harías la resta al revés y al resultado le pones signo negativo en este caso serian menos 40 grados y 3 minutos.
25,56 dam+ 526,9 dm. Lo tengo que llevar todo a metro qué resultado daría?