La medida fundamental para medir volúmenes es el metro cúbico.
Otras unidades de volúmenes son:
| Medida | Símbolo | Equivalencia |
|---|---|---|
| kilómetro cúbico |  |  |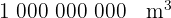
| Hectómetro cúbico |  |  |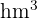
| Decámetro cúbico |  |  |
| Metro cúbico |  |  |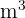
| Decímetro cúbico |  |  |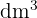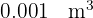
| Centímetro cúbico |  |  |
| Milímetro cúbico |  |  |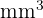
Observamos que desde los submúltiplos, en la parte inferior, hasta los múltiplos, en la parte superior, cada unidad vale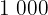 
más que la anterior.
Si queremos pasar de una unidad a otra tenemos que: multiplicar (si es de una unidad mayor a otra menor) o dividir (si es de una unidad menor a otra mayor) por la unidad seguida de tantos tríos de ceros como lugares haya entre ellas.
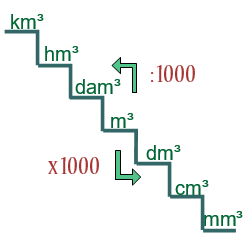
Ejemplos:
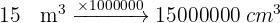
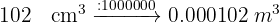
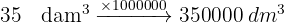
Ejemplos de conversión de medidas
1 Pasar 
a :
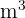Tenemos que multiplicar (porque el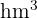 
es mayor que el 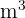) por la unidad seguida de seis ceros, ya que hay dos lugares entre ambos.
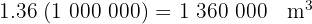
2 Pasar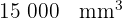 
a :
Tenemos que dividir (porque el 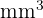es menor que el por la unidad seguida de tres ceros, ya que hay un lugar entre ambos.
Relación entre unidades de capacidad, volumen y masa
Existe una relación muy directa entre el volumen y capacidad.
Ejemplo:
es la capacidad que contiene un recipiente cúbico de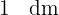 
de arista; es decir, la capacidad contenida en un volumen de 
.
También existe una relación entre el volumen y la masa de agua.
Ejemplo:
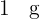equivale a 
de agua pura a 
.
Analicemos las relaciones que existen entre capacidad, volumen y masa (de agua):
| Capacidad | Volumen | Masa (de agua) |
|---|---|---|
 | |  |
| |  |
 | | |
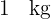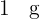Ejemplos de relaciones entre capacidad, volumen y masa
Expresa en litros:
1 
2 
3 
4 
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
muy bueno pero muy largo y cuando te corrige no se alcanza a leer, esta muy chica la letra
Hola agradecemos tus comentarios, en cuanto a lo largo es para ser mas explícitos y en cuanto a la letra pequeña estamos trabajando en ello.
yo quisiera que en la pagina se pudiera resolver los ejercicios
Hola podría ser buena idea la que propones, podrias darnos mas detalles al respecto y posiblemente en un futuro poder cumplir con esta sugerencia tuya.
Hola, cómo se resolvería la resta en el sistema sexagesimal si el minuendo, en grados, es menor que el sustraendo? La profesora dice debe pedir prestado un giro que es igual a 360° y de esa manera resolver.
Hola respondiendo a tu pregunta imagina que a 36 grados y 27 minutos le restas 76 grados y 30 minutos, simplemente harías la resta al revés y al resultado le pones signo negativo en este caso serian menos 40 grados y 3 minutos.
25,56 dam+ 526,9 dm. Lo tengo que llevar todo a metro qué resultado daría?
Ya existen artículos con temas que ya mencionas, en el buscador escribe el tema proporción y saldran los articulos.