A través de la resolución de estos ejercicios interactivos, podremos profundizar en la comprensión de conceptos clave como la energía cinética, la energía potencial, el trabajo realizado por fuerzas conservativas y no conservativas, así como también la aplicación de la ley de la conservación de la energía.
Un objeto de masa m se deja caer desde una altura h. Si no se considera la fricción, los valores de las energía potencial y cinética en la altura h son...
Selecciona una respuesta.
1La energía total de un sistema sin fricción es
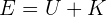
donde
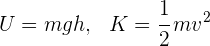
2Como no se imprime velocidad al objeto, su velocidad inicial es cero, de donde se tiene que
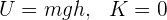
Se deja caer un objeto de masa m desde una altura h, hasta que choca con el piso con velocidad 
. Si se desprecia la fricción, entonces se cumple...
Selecciona una respuesta.
1De la ley de la conservación de la energía se cumple
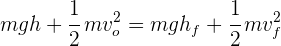
2Como no se imprime velocidad al objeto, su velocidad inicial es cero y como choca con el piso su altura final también es cero, de donde se tiene que
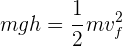
Una bola de demolición de 50 kg se impulsa lateralmente hasta que queda por arriba de su posición más baja. Si la velocidad en su punto más bajo es de 6 m/s y se desprecia la fricción, la altura a la que debe soltarse la bola de demolición es...
Selecciona una respuesta.
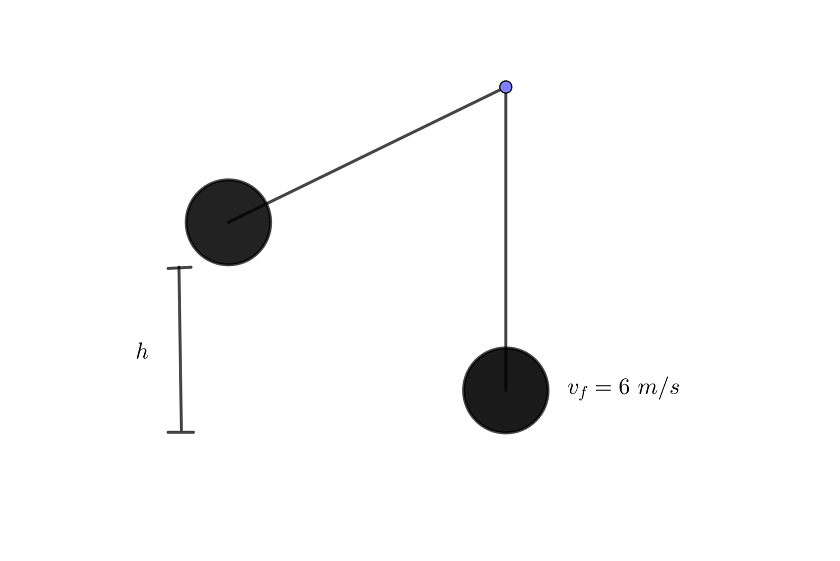
1Por la conservación de la energía, la energía total en los puntos inicial y final es la misma
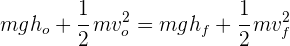
2En el punto inicial, la velocidad es cero y la altura h es deconocida. En el punto final, la altura es cero y la velocidad es de 6 m/s. Sustituimos los datos en la ecuación anterior
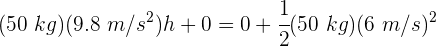
3Despejamos la altura y se obtiene
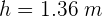
Un objeto de 10 kg se suelta desde una altura de 15 m. Si se desprecia la fricción del aire, la velocidad de choque con el suelo es...
Selecciona una respuesta.
1Por la conservación de la energía, la energía total en los puntos inicial y final es la misma
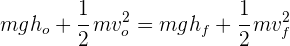
2En el punto inicial, la velocidad es cero y la altura es 15 m. En el punto final, la altura es cero y no conocemos la velocidad. Sustituimos los datos en la ecuación anterior
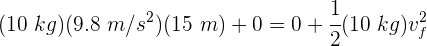
3Despejamos la velocidad final y se obtiene
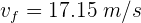
Un objeto de 7 kg se lanza a 2 m/s desde una altura de 10 m. Si se desprecia la fricción del aire, la velocidad de choque con el suelo es...
Selecciona una respuesta.
1Por la conservación de la energía, la energía total en los puntos inicial y final es la misma
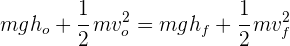
2En el punto inicial, la velocidad no es cero y la altura es 10 m. En el punto final, la altura es cero y no conocemos la velocidad. Sustituimos los datos en la ecuación anterior
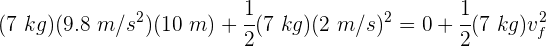
3Despejamos la velocidad final y se obtiene
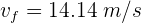
Un objeto de 2 kg se lanza hacia arriba y alcanza una altura de 5 m. La velocidad inicial con la que se lanza el objeto es...
Selecciona una respuesta.
1Por la conservación de la energía, la energía total en los puntos inicial y final es la misma
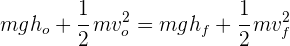
2En el punto final, la velocidad es cero y la altura es 5 m. En el punto inicial, la altura es cero y no conocemos la velocidad. Sustituimos los datos en la ecuación anterior
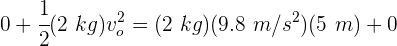
3Despejamos la velocidad inicial y se obtiene
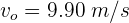
Un objeto esférico de 5 kg se desliza por una pendiente de 7 metros de altura. Si desde el punto más alto inicia su descenso a 1.5 m/s, su velocidad en el punto más bajo es...
Selecciona una respuesta.
1Por la conservación de la energía, la energía total en los puntos inicial y final es la misma
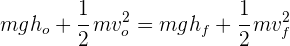
2En el punto final, la masa es 5 kg, la altura es cero y no conocemos la velocidad. En el punto inicial, la altura es 7 m y la velocidad es 1.5 m/s. Sustituimos los datos en la ecuación anterior
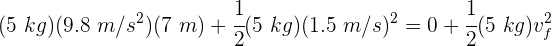
3Despejamos la velocidad final y se obtiene
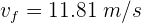
Un bloque de 10 kg descansa sobre un plano inclinado de 9 m de longitud y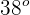 
de inclinación. Si la velocidad al pie del plano inclinado es de 9 m/s, el coeficiente de fricción cinética es...
Selecciona una respuesta.
1 Dibujamos el diagrama de equilibrio
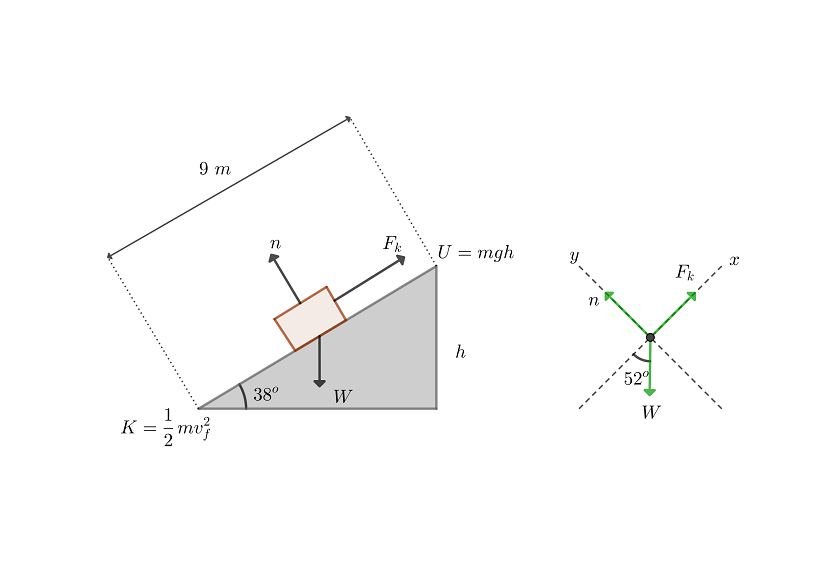
2Escribimos la ecuación de la conservación de la energía en términos generales
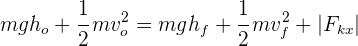
3Como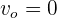 
y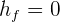 
, la ecuación de la conservación de la energía en términos generales se reduce a
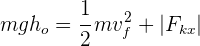
4Calculamos la altura inicial
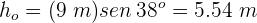
5Calculamos la fuerza normal. Del diagrama de cuerpo libre se tiene
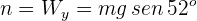
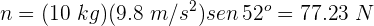
6entonces, la fuerza de fricción se expresa
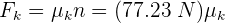
7 Sustituimos en la ecuación de conservación de la energía
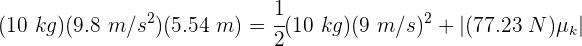
8Despejando el coeficiente de fricción cinética, se obtiene
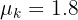
Un trineo de 50 kg descansa sobre un plano inclinado de 150 m de longitud y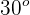 
de inclinación. Si 
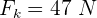, la energía total en el punto más bajo es...
Selecciona una respuesta.
1 Dibujamos el diagrama de equilibrio
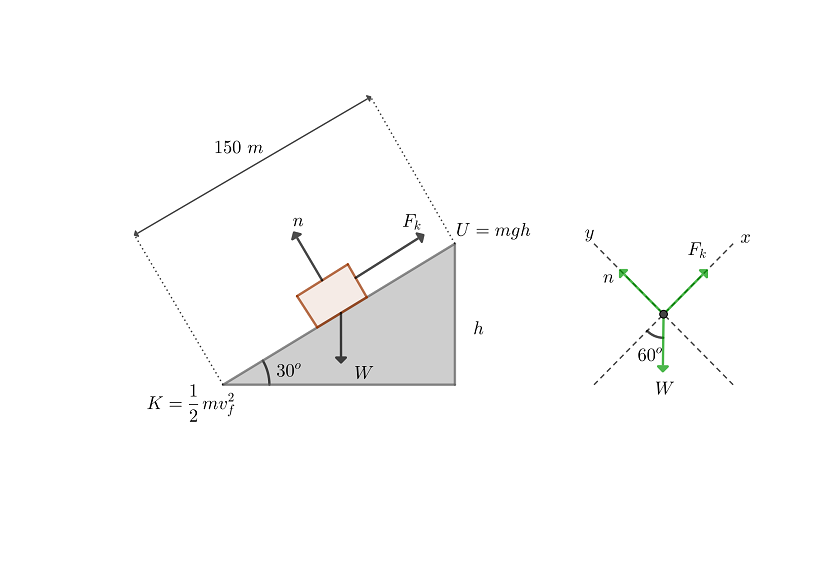
2Escribimos la ecuación de la energía total
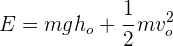
3Como 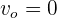, la ecuación de la energía se reduce a
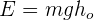
4Calculamos la altura inicial
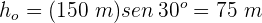
5 Sustituimos en la ecuación de la energía
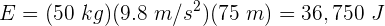
6Por la conservación de la energía, la energía en el púnto más bajo es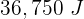 
Un ciclista en su bicicleta tienen juntos una masa de 70 kg y parten del reposo en la cumbre de una pendiente de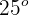 
de inclinación. Si 
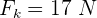, encuentra la distancia que habrá recorrido el carro cuando su velocidad alcance 13 m/s...
Selecciona una respuesta.
1 Dibujamos el diagrama de equilibrio
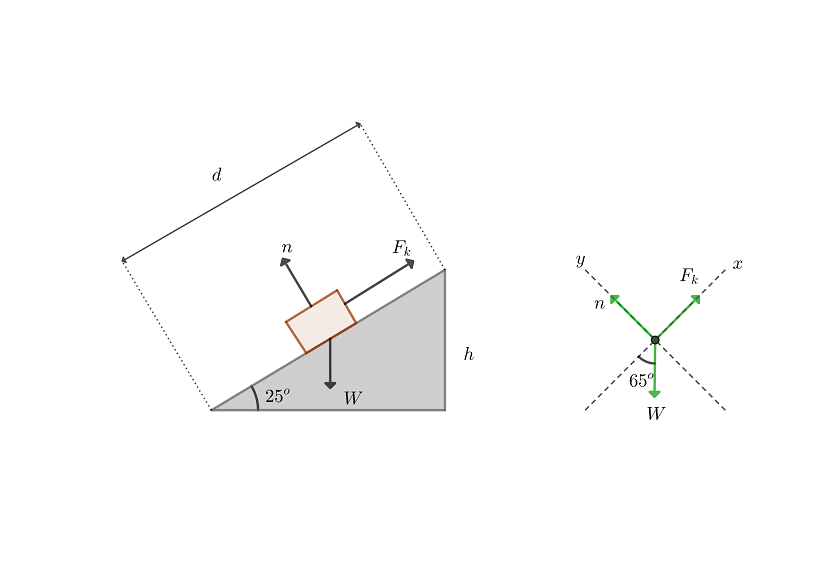
2Escribimos la ecuación de la conservación de la energía en términos generales
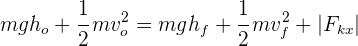
3 Sustituimos en la ecuación de conservación de la energía
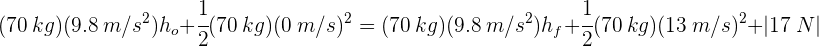
4Despejando las alturas, se obtiene
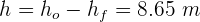
5Calculamos la distancia recorrida
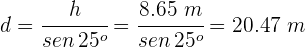
Si tienes dudas puedes consultar ejercicios resueltos del tema.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.