La teoría de la relatividad, propuesta por Albert Einstein a principios del siglo XX, revolucionó nuestra comprensión del espacio, el tiempo y la gravedad. En el ámbito de la cinemática relativista, que se ocupa del movimiento de objetos a velocidades cercanas a la velocidad de la luz, los fenómenos observados difieren significativamente de las predicciones de la mecánica clásica.
Los ejercicios resueltos que presentaremos a continuación exploran situaciones de mecánica clásica para velocidades no relativistas y algunos ejercicios de simultaneidad de cinemática relativista.
Dos automóviles se encuentran en extremos opuestos A y B de un camino recto. El automóvil en A se mueve a 50 km/h en dirección a B, mientras que el automóvil que se encuentra en B se mueve a 60 km/h en dirección a A. Encuentra la velocidad del segundo automóvil respecto al primero.
1 Los automóviles se mueven de frente uno hacia el otro. El primer automóvil se mueve a velocidad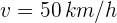 
y el segundo automóvil se mueve a velocidad 
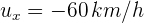, ya que se mueve en dirección contraria al primero
2Denotamos por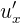 
a la velocidad del segundo automóvil medida por el conductor del primer auto.
3Utilizamos la transformación de velocidad de Galileo
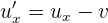
4Sustituimos los datos conocidos
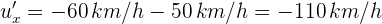
Así, la velocidad del segundo automóvil respecto del primero es -110 km/h. El signo negativo indica que la dirección del segundo automóvil es contraria a la del primero.
Dos automóviles se mueven en la misma dirección y sentido. El automóvil A se mueve a 80 km/h y el automóvil B se mueve a 100 km/h. ¿Cuál es la velocidad de A respecto de B?
1 El automóvil B se mueve a velocidad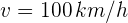 
y A se mueve a velocidad 
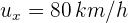, ya que se mueven en la misma dirección
2Denotamos por 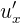a la velocidad de A respecto de B
3Utilizamos la transformación de velocidad de Galileo
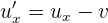
4Sustituimos los datos conocidos
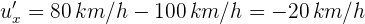
Así, la velocidad de A respecto a B es negativa, ya que después de coincidir, A se queda detras de B.
Un oficial de tránsito se encuentra parado en una calle y ve pasar dos automóviles A y B en sentidos opuestos, ambos a 30 km/h. ¿Cuál es la velocidad de los dos automóviles respecto al oficial de tránsito?
1 Elegimos la dirección de A como positiva, entonces este se mueve a velocidad 30 km/h y B a -30 km/h
2Calculamos la velocidad de A respecto al oficial. Denotamos por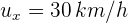 
la velocidad de A, 
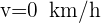la velocidad del oficial y 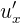a la velocidad de A respecto del oficial
3Utilizamos la transformación de velocidad de Galileo
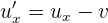
4Sustituimos los datos conocidos
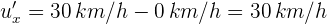
5Calculamos la velocidad de B respecto al oficial. Denotamos por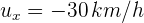 
la velocidad de B, 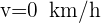la velocidad del oficial y 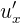a la velocidad de B respecto del oficial
6Sustituimos los datos conocidos en la fórmula de transformación de velocidad de Galileo
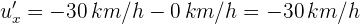
Un automóvil se mueve el línea recta a 30 km/h. Una persona en la parte trasera lanza una pelota a 10 km/h en sentido contrario al movimiento del vehículo. ¿Cuál es la velocidad de la pelota respecto al conductor del automóvil?
1 Elegimos la dirección del automóvil como positiva, entonces este se mueve a velocidad 30 km/h y la pelota a -10 km/h
2Calculamos la velocidad de la pelota respecto al conductor del vehículo. Denotamos por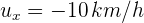 
la velocidad de la pelota, 
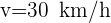la velocidad del automóvil y 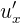a la velocidad de la pelota respecto del conductor
3Utilizamos la transformación de velocidad de Galileo
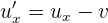
4Sustituimos los datos conocidos
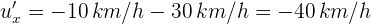
Así, el conductor ve que la pelota se mueve a 40 km/h en dirección contraria al del automóvil
Un automóvil se mueve el línea recta a 30 km/h. Una persona en la parte trasera dispara un proyectil a 100 km/h en el mismo sentido del movimiento del vehículo. ¿Cuál es la velocidad del proyectil respecto al conductor del automóvil?
1 Elegimos la dirección del automóvil como positiva, entonces este se mueve a velocidad 30 km/h y el proyectil a 100 km/h
2Calculamos la velocidad del proyectil respecto al conductor del vehículo. Denotamos por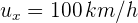 
la velocidad del proyectil, 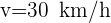la velocidad del automóvil y 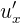a la velocidad del proyectil respecto del conductor
3Utilizamos la transformación de velocidad de Galileo
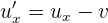
4Sustituimos los datos conocidos
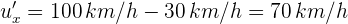
Así, el conductor ve que el proyectil se mueve a 70 km/h en la misma dirección del automóvil
Una persona se encuentra en el andén de la estación del tren. En ese momento pasa el tren a 70 km/h y en el interior de un vagón un pasajero lanza una pelota a 20 km/h en el misma dirección de movimiento del tren. Hallar la velocidad de la pelota respecto de la persona en el andén.
1 Elegimos la dirección del tren como positiva, entonces este se mueve a velocidad 70 km/h y la pelota a 20 km/h
2 Del diagrama general de posición de Galileo se tiene
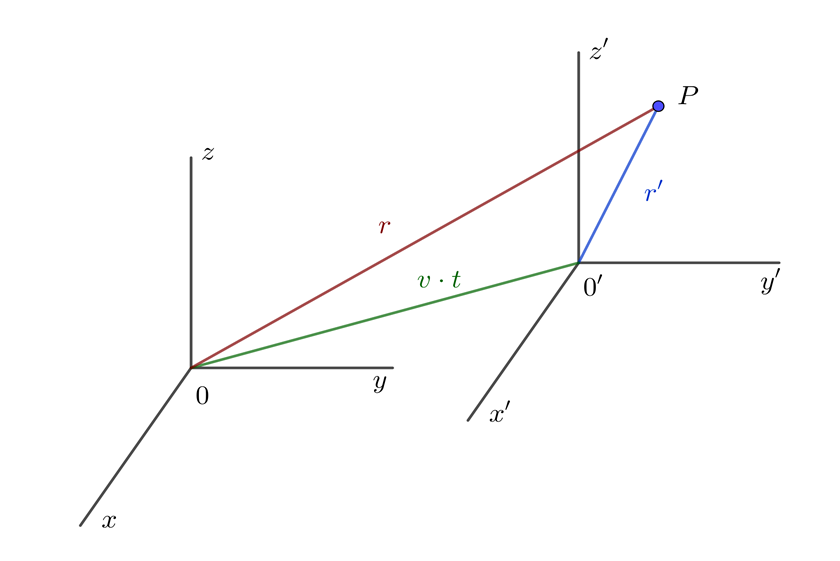
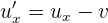
3Calculamos la velocidad de la pelota respecto a la persona en el andén. Denotamos por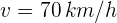 
la velocidad del tren respecto a la persona en el anden, 
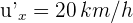la velocidad de la pelota respecto al pasajero y 
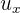la velocidad de la pelota respecto de la persona en el andén
4Sustituimos los datos conocidos en la transformación de Galileo
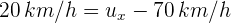
Así, se obtiene que la persona en el andén ve que la pelota se mueve a 90 km/h en la misma dirección que el tren.
Un pasajero de un tren se encuentra en el punto medio de un vagón y enciende una linterna de manera que la luz se propaga hacia las puertas trasera y delantera. Realiza un diagrama espacio-tiempo simultáneo para el pasajero y un observador en el andén.
1 Expresamos los puntos en el diagrama espacio-tiempo para el pasajero del tren y notamos que A y B son simultáneos en S'
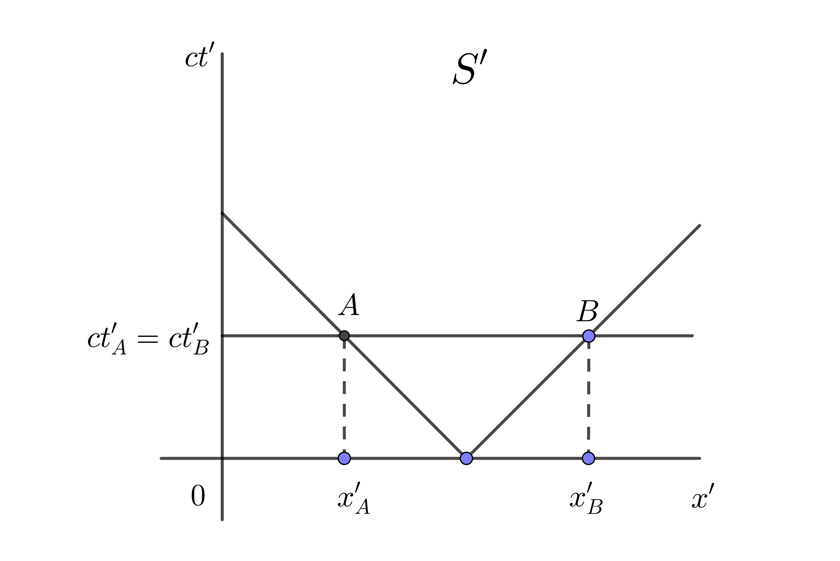
2 Expresamos los puntos en el diagrama espacio-tiempo para el observador en el andén y notamos que A y B no son simultáneos en S
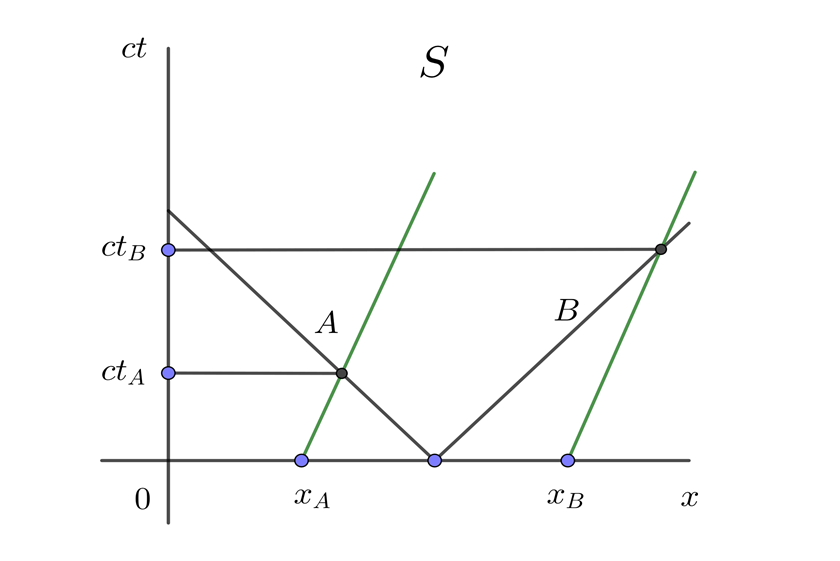
3 Expresamos S y S' en el diagrama espacio-tiempo
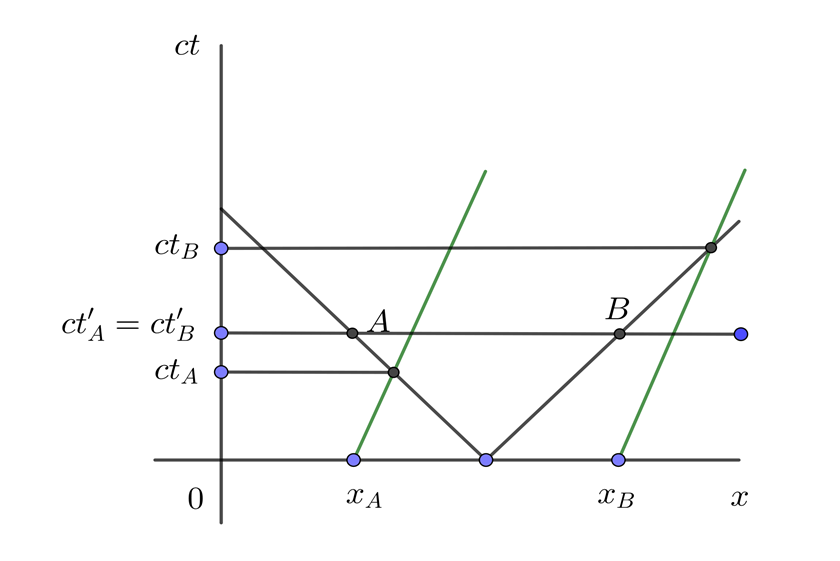
Una persona se encuentra en el andén de la estación del tren. En ese momento pasa el tren a 80 km/h y en el interior de un vagón un pasajero que se encuentra sentado ve pasar un niño caminando a 2 km/h en el misma dirección de movimiento del tren. Hallar la velocidad del niño respecto de la persona en el andén.
1 Elegimos la dirección del tren como positiva, entonces este se mueve a velocidad 80 km/h y la del niño a 2 km/h
2 Del diagrama general de posición de Galileo se tiene
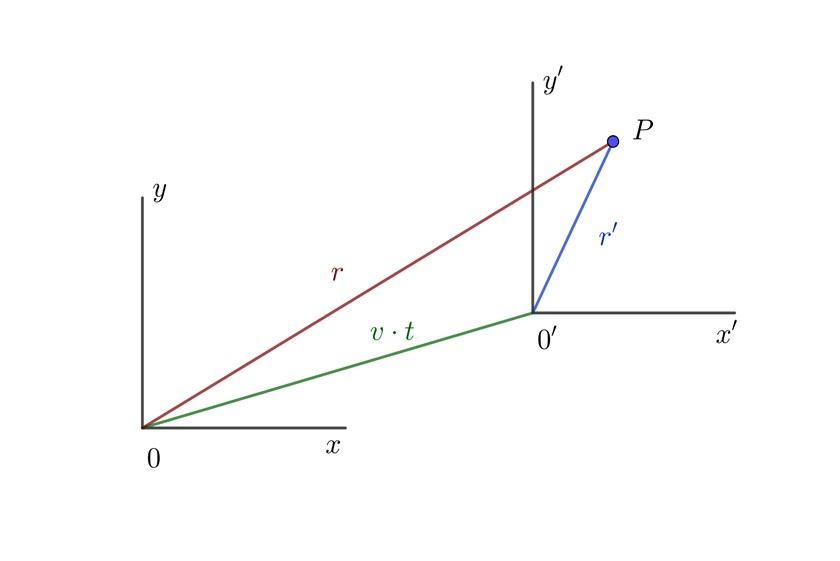
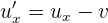
3Calculamos la velocidad del niño respecto a la persona en el andén. Denotamos por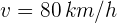 
la velocidad del tren respecto a la persona en el anden, 
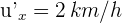la velocidad del niño respecto al pasajero y 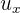la velocidad del niño respecto de la persona en el andén
4Sustituimos los datos conocidos en la transformación de Galileo
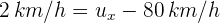
Así, se obtiene que la persona en el andén ve que el niño se mueve a 82 km/h en la misma dirección que el tren.
Una persona se encuentra en el andén de la estación del tren. En ese momento pasa el tren a 40 m/s y en el interior de un vagón se encuentra sentado un pasajero. 20 segundos después, la persona en el andén ve pasar un pájaro volando a lo largo de las vías en la misma dirección que el tren se encuentra a 500 metros. ¿Cuáles son las coordenadas del pájaro estimadas por el pasajero?
1 Las coordenadas del pájaro para la persona en el anden son
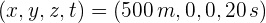
2 Del diagrama general de posición de Galileo se tiene
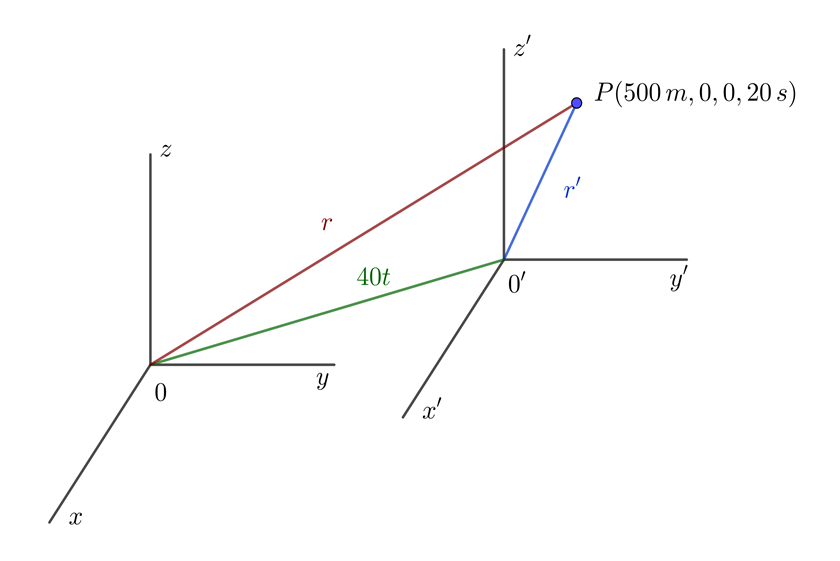
3Las coordenadas de transformación del pájaro para el pasajero en el tren
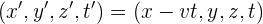
4Sustituimos los datos conocidos
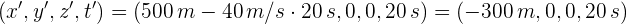
Una persona se encuentra en el andén de la estación del tren. En ese momento pasa el tren a 40 m/s y en el interior de un vagón se encuentra sentado un pasajero el cual ve volando un proyectil en el interior del vagón a 2 m/s en dirección contraria al movimiento del tren. ¿Cuál es la velocidad del proyectil respecto a la persona en el andén?
1 Elegimos la dirección del tren como positiva, entonces este se mueve a velocidad 40 m/s y el proyectil a -2 m/s
2Calculamos la velocidad del proyectil respecto a la persona en el andén. Denotamos por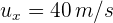 
del tren, 
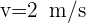la velocidad del proyectil y 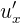a la velocidad del proyectil respecto de la persona en el andén
3Utilizamos la transformación de velocidad de Galileo
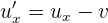
4Sustituimos los datos conocidos
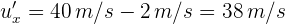
Así, la persona en el andén ve que el proyectil se mueve a 38 m/s en la misma dirección del tren
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.