¡Bienvenidos al fascinante mundo de las leyes de Newton! En este conjunto de ejercicios resueltos, exploraremos las fundamentales leyes que gobiernan el movimiento de los objetos en nuestro universo. Sir Isaac Newton revolucionó nuestra comprensión del movimiento y la interacción de las fuerzas, estableciendo tres leyes que son la base de la mecánica clásica.
A través de estos ejercicios, descubriremos cómo aplicar las leyes de Newton para entender y predecir el comportamiento de los objetos en reposo y en movimiento. Desde el análisis de fuerzas hasta la determinación de aceleraciones y la resolución de problemas prácticos.
Un automóvil se mueve a una velocidad constante de 50 km/h. Encuentra la velocidad neta.
1 La primera ley de Newton dice que un cuerpo en reposo permanece en reposo, o si se encuentra en movimiento con velocidad constante permanece en movimiento, a menos que una fuerza neta actue sobre él.
2 Como el automóvil se encuentra en movimiento con velocidad constante, entonces la fuerza neta sobre él es cero. Notamos que el automóvil tiene una fuerza de avance hacia el frente, pero tambien existe una fuerza contraria llamada fuerza de fricción que tiene la misma magnitud y dirección contraria a la fuerza de avance, de modo que la fuerza neta es cero.
Una lámpara de 5 kg cuelga de un alambre empotrado en el techo. ¿Cuál es la tensión en el alambre?
1 Dibujamos el diagrama de equilibrio
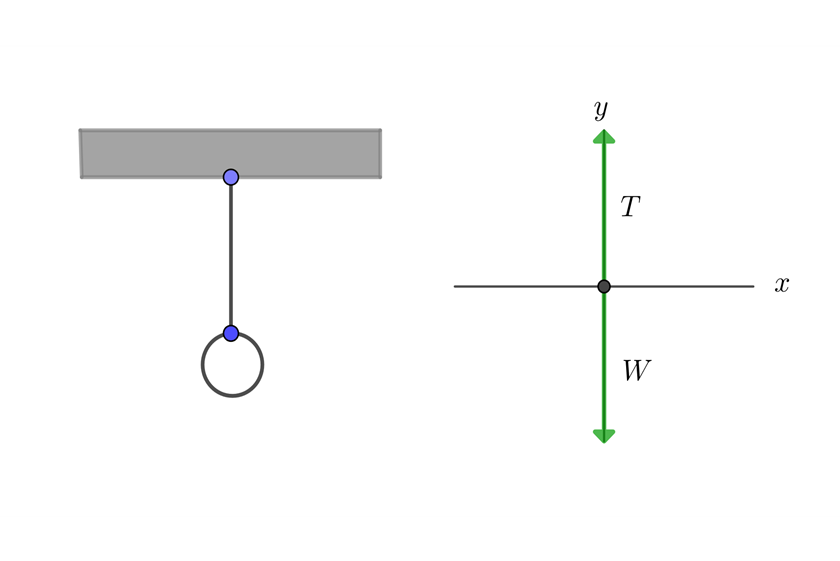
2Conocemos la masa de lámpara, por lo que calculamos su peso W
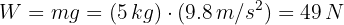
3Calculamos la fuerza neta vertical, ya que no hay fuerzas horizontales actuando
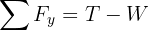
4Como el sistema se encuentra en equilibrio, la fuerza neta es igual a cero
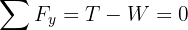
5Despejando se obtiene T=49 N
Observa que al estar en equilibrio, la fuerza neta es cero por lo que ambas fuerzas al ser opuestas, estas son iguales en magnitud.
Un cable empotrado en el techo sostiene un objeto de masa m, el cual tiene un cable que sostiene otro objeto que tiene la mitad de su masa. ¿Cuál es la tensión en los cables?
1 Dibujamos el diagrama de equilibrio
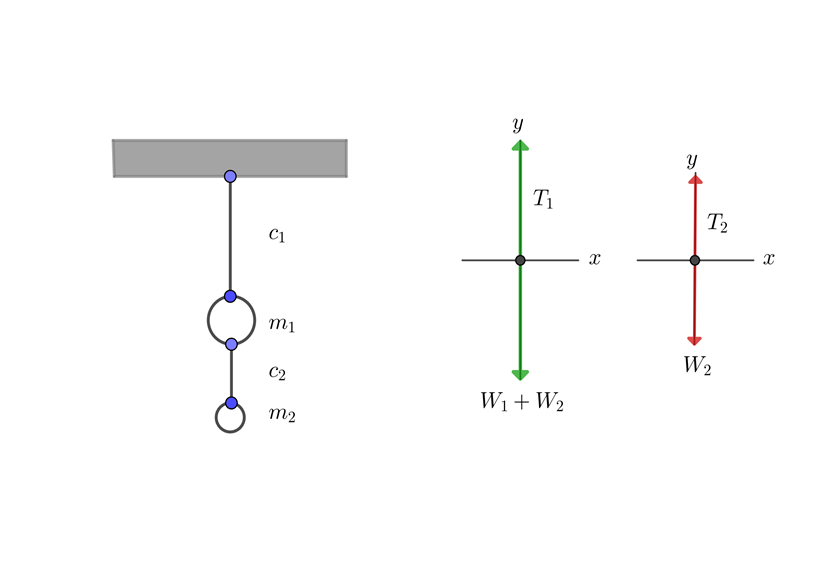
2Conocemos la masa de los objetos, por lo que calculamos su peso
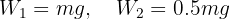
3Calculamos la fuerza neta vertical para el primer sistema, ya que no hay fuerzas horizontales actuando
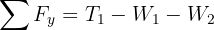
4Como el sistema se encuentra en equilibrio, la fuerza neta es igual a cero
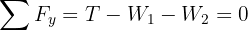
5Despejando se obtiene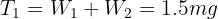 
6 Para el segundo sistema donde interactúan el segundo cable y la segunda masa, dado que la fuerza neta es cero, entonces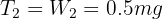 
Una caja suspendida por una cuerda es jalada hacia la derecha en forma horizontal con otra cuerda y sostenida de forma que la primera cuerda forma un ángulo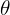 
con un el techo. Si la caja tiene masa m, encuentra las tensiones en ambas cuerdas.
1 Dibujamos el diagrama de equilibrio
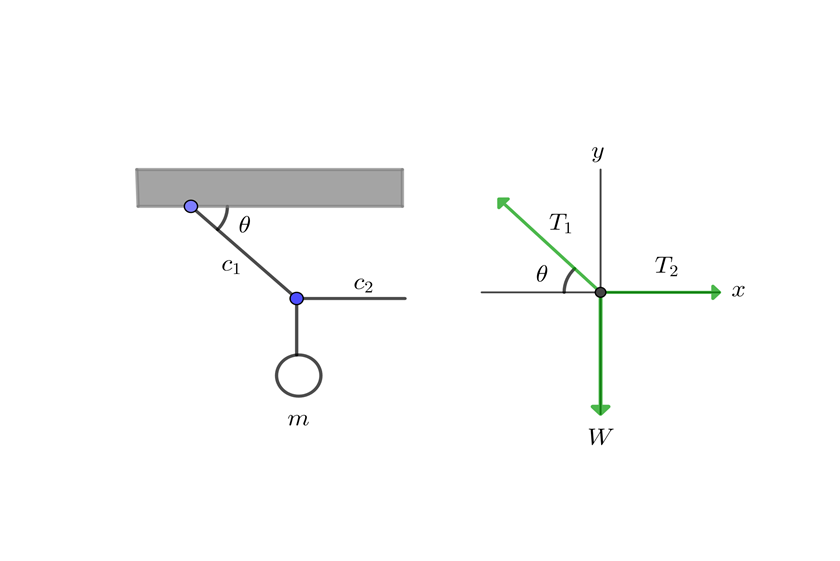
2Conocemos la masa de caja, por lo que calculamos su peso y calculamos las componentes de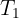 
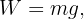
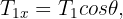
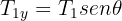
3Calculamos la fuerza neta horizontal y vertical
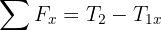
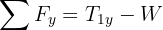
4Como el sistema se encuentra en equilibrio, las fuerzas netas son iguales a cero
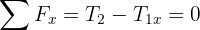
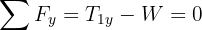
5Despejando 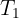en la fuerza neta vertical, se obtiene
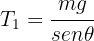
6Despejando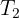 
en la fuerza neta horizontal, se obtiene
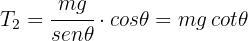
Una piñata suspendida por una cuerda es jalada hacia la derecha en forma horizontal con otra cuerda y sostenida de forma que la primera cuerda forma un ángulo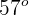 
con un el techo. Si el peso de la piñata es 9.8 N, encuentra las tensiones en ambas cuerdas.
1 Dibujamos el diagrama de equilibrio
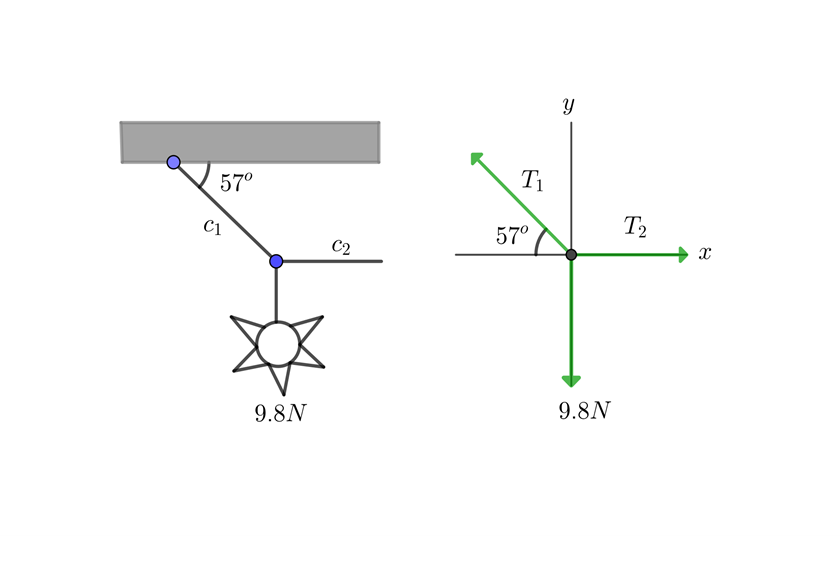
2Calculamos su peso y calculamos las componentes de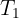
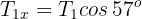
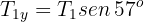
3Calculamos la fuerza neta horizontal y vertical
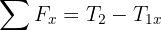
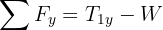
4Como el sistema se encuentra en equilibrio, las fuerzas netas son iguales a cero
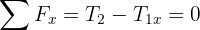
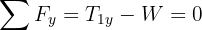
5Despejando 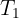en la fuerza neta vertical, se obtiene
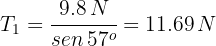
6Despejando 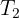en la fuerza neta horizontal, se obtiene
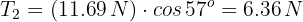
Un objeto cuelga de una cuerda unida a otras dos cuerdas fijas a un techo, de manera que se forma un triángulo. Si la caja tiene un peso W y los ángulos de las dos cuerdas con el techo son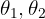 
respectivamente, encuentra las tensiones de las tres cuerdas.
1 Dibujamos el diagrama de equilibrio
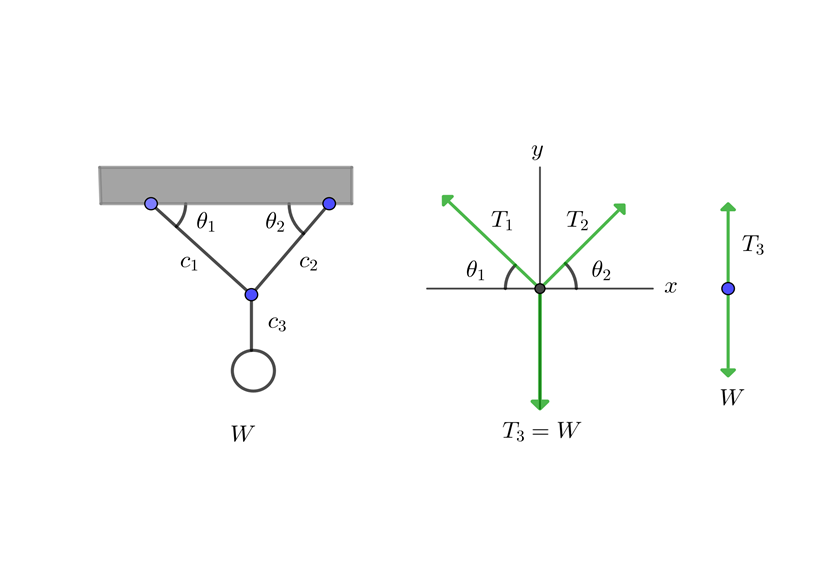
2Del sistema vertical formado por el objeto y la cuerda tres, se obtiene
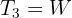
3Considerando las tres cuerdas, se tiene un sistema cuyas componentes son
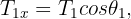
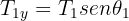
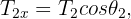
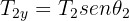
4Calculamos la fuerza neta horizontal y vertical
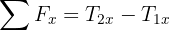
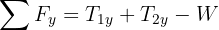
5Como el sistema se encuentra en equilibrio, las fuerzas netas son iguales a cero
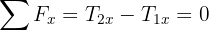
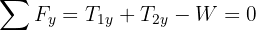
6En términos de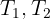 
el sistema de ecuaciones obtenido es
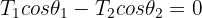
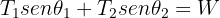
7Resolviendo el sistema para 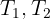, se obtiene
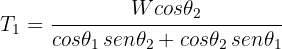
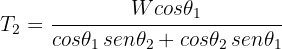
Un objeto cuelga de una cuerda unida a otras dos cuerdas fijas a un techo, de manera que se forma un triángulo. Si la caja tiene un peso de 100 N y los ángulos de las dos cuerdas con el techo son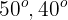 
respectivamente, encuentra las tensiones de las tres cuerdas.
1 Dibujamos el diagrama de equilibrio
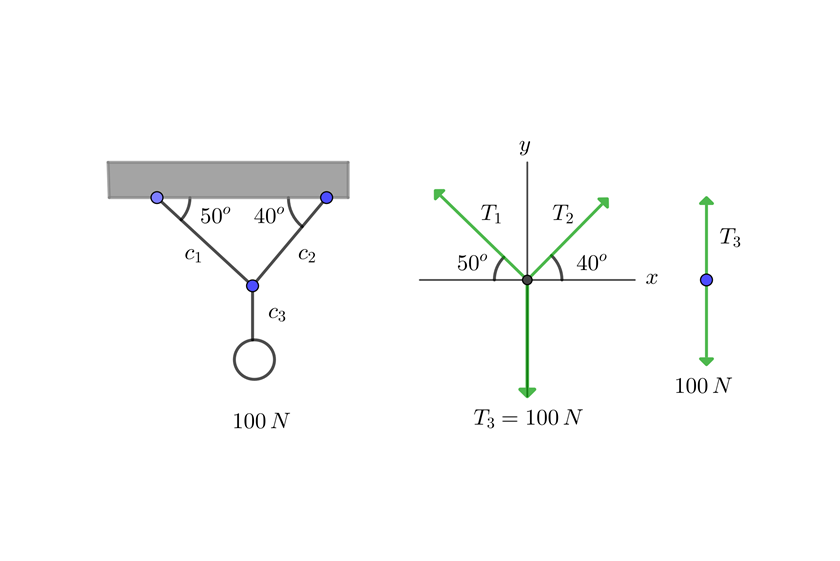
2Notamos que se cumplen las condicones de problema 6, por lo que sustituimos en las fórmulas encontradas en dicho ejercicio
Un objeto de peso W se encuentra sobre un plano inclinado sin fricción, que tiene pendiente 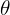. El objeto está atado a una cuerda que pasa sobre una polea sin fricción colocada en el extremo superior del plano y que va atada a un bloque. Si el sistema se encuentra en equilibrio, hallar el peso del bloque.
1 Dibujamos el diagrama de equilibrio
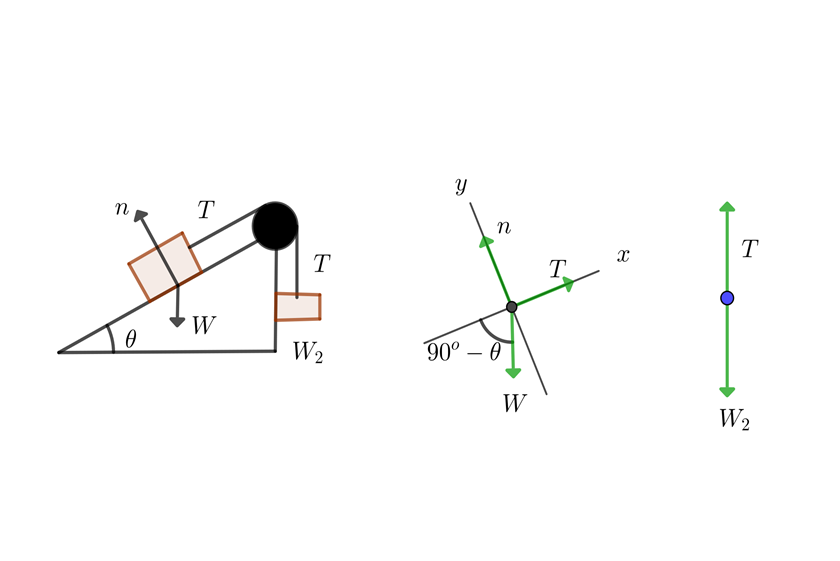
2Del sistema vertical formado por el objeto y la cuerda, se obtiene
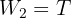
3Considerando el objeto sobre el plano inclinado, se tiene un sistema cuyas componentes del peso son
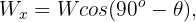
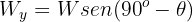
4Calculamos la fuerza neta horizontal y vertical
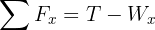
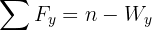
5Como el sistema se encuentra en equilibrio, las fuerzas netas son iguales a cero
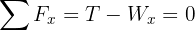
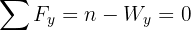
6De la primera ecuación se tiene que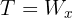 
, luego el peso del bloque es
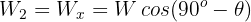
Un objeto de peso 50 N se encuentra sobre un plano inclinado sin fricción, que tiene pendiente 
. El objeto está atado a una cuerda que pasa sobre una polea sin fricción colocada en el extremo superior del plano y que va atada a un bloque. Si el sistema se encuentra en equilibrio, hallar el peso del bloque.
1 Dibujamos el diagrama de equilibrio
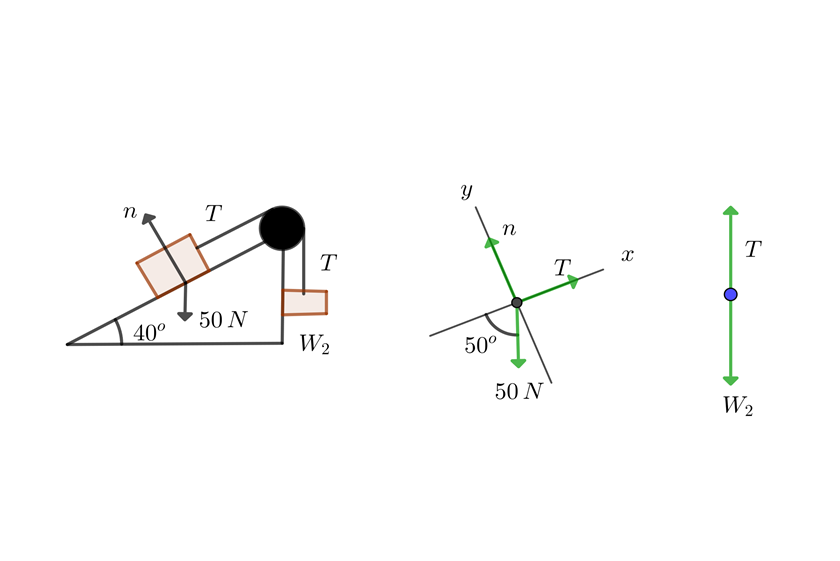
2Notamos que se cumplen las condicones de problema 8, por lo que sustituimos en la fórmula encontrada en dicho ejercicio
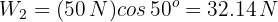
Un objeto se encuentra sobre un plano inclinado sin fricción, que tiene pendiente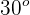 
. El objeto está atado a una cuerda que pasa sobre una polea sin fricción colocada en el extremo superior del plano y que va atada a un bloque de 100 N. Si el sistema se encuentra en equilibrio, hallar el peso del objeto sobre el plano.
1 Dibujamos el diagrama de equilibrio
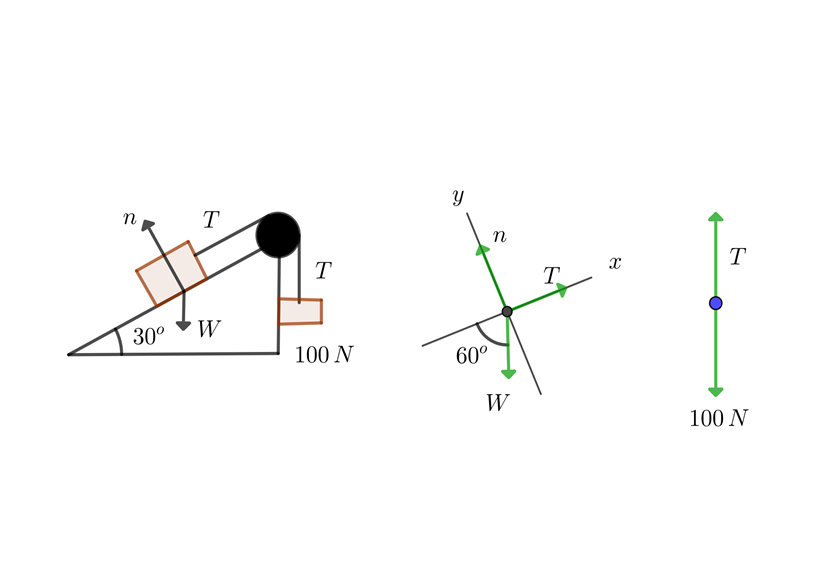
2Notamos que se cumplen las condicones de problema 8, por lo que sustituimos en las fórmulas encontradas en dicho ejercicio y despejamos el peso
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.