En los siguientes ejercicios resueltos, exploraremos cómo aplicar las fórmulas de cantidad de movimiento lineal y angular y exploraremos su relación con la segunda ley de Newton.
Un objeto de 50 kg se mueve a una velocidad de 4 m/s. Encuentra el momento del objeto.
1Escribimos los elementos conocidos

2Empleamos la fórmula de momento lineal
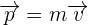
3 Sustituimos los datos conocidos en la fórmula de momento lineal y se obtiene
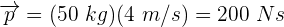
Un objeto de 10 kg tiene un momento lineal de 15 Ns. Encuentra la velocidad del objeto.
1Escribimos los elementos conocidos
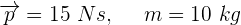
2Empleamos la fórmula de momento lineal
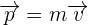
3 Sustituimos los datos conocidos en la fórmula de momento lineal
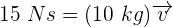
4 Despejando la velocidad se obtiene
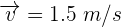
Una persona camina a una velocidad de 2 m/s. Encuentra la masa de la persona si tiene momento lineal de 100 Ns.
1Escribimos los elementos conocidos
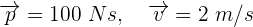
2Empleamos la fórmula de momento lineal
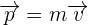
3 Sustituimos los datos conocidos en la fórmula de momento lineal
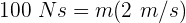
4 Despejando la masa se obtiene
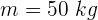
Dos automóviles se mueven a la misma velocidad. Si la masa del primer automóvil es mayor que la masa del segundo automóvil, ¿cómo son los momentos lineales de ambos autos?
1Escribimos los elementos conocidos con subíndice 1 para el primer automóvil y subíndice 2 para el segundo

2Multiplicamos la desigualdad por la velocidad del primer automóvil

3Como la velocidad es la misma para ambos automóviles

4Empleamos la fórmula de momento lineal
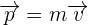
5 Se obtiene

6 Así, el momento lineal del primer auto es mayor que el momento lineal del segundo
Un auto de fórmula uno con 700 kg de masa parte del reposo y después de 5 segundos alcanza una velocidad de 28 m/s. Encuentra el cambio en la cantidad de momento.
1Escribimos los elementos conocidos
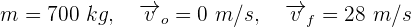
2Empleamos la fórmula de cambio de cantidad de momento lineal
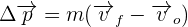
3 Sustituimos los datos conocidos en la fórmula anterior
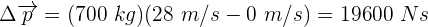
¿Qué se obtiene de derivar el momento lineal con respecto al tiempo?
1 Expresamos la derivada del momento lineal respecto al tiempo
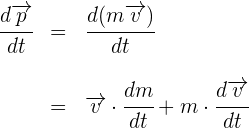
2Consideramos la masa constante, es decir, es la misma para cualquier tiempo, entonces su derivada es cero y se tiene
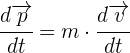
3Como la derivada de la velocidad respecto al tiempo es igual a la aceleración, se tiene
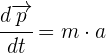
4Por la segunda ley de Newton se tiene que la masa por la aceleración es igual a la fuerza, por lo que la derivada del momento lineal respecto al tiempo es igual a la fuerza del objeto/p>
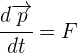
Una partícula de 5 g gira con una velocidad tangencial de 3 m/s sobre el extremo de un círculo de radio 1 m. Encuentra la magnitud del momento angular de la partícula.
1Escribimos los elementos conocidos
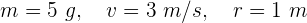
2Empleamos la fórmula de la magnitud del momento angular
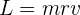
3 Sustituimos los datos conocidos en la fórmula anterior, sin olvidar expresar la masa en kilogramos
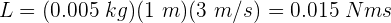
Recuerda que
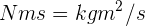
Un ciclista de 50 kg se mueve sobre su bicicleta de 5 kg en una pista circular de radio 15 m con una velocidad tangencial de 17 m/s. Encuentra la magnitud de su momento angular.
1Escribimos los elementos conocidos, considerando la masa total del ciclista en la bicicleta
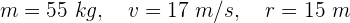
2Empleamos la fórmula de la magnitud del momento angular
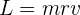
3 Sustituimos los datos conocidos en la fórmula anterior, sin olvidar expresar la masa en kilogramos
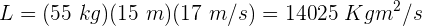
David empleó una piedra en una onda de 0.5 m a la cual le imprimió una velocidad tangencial de 34 m/s. Si la magnitud del momento angular es de 0.34 Nms, encuentra la masa de la piedra.
1Escribimos los elementos conocidos
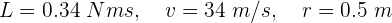
2Empleamos la fórmula de la magnitud del momento angular
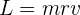
3 Sustituimos los datos conocidos en la fórmula anterior
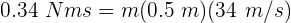
4 Despejamos la masa y se obtiene
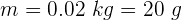
Una partícula de 0.5 kg se mueve en el plano con una velocidad 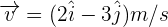 . Encuentra la cantidad de movimiento angular de la partícula cuando su vector de posición es
. Encuentra la cantidad de movimiento angular de la partícula cuando su vector de posición es 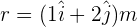 .
.
1Escribimos los elementos conocidos
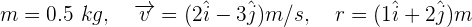
2Empleamos la fórmula del momento angular
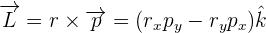
3Calculamos el momento lineal
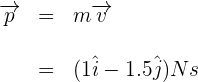
4 Sustituimos los datos conocidos y el momento lineal en la fórmula de momento angular
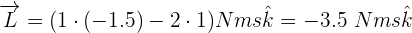
Resumir con IA:



Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.