Capítulos
La fuerza, masa y aceleración son tres conceptos que a menudo tomamos en cuenta para realizar cualquier acción en la vida diaria. Por ejemplo, para realizar sentadillas, hablamos de cuánta fuerza debemos realizar con las piernas para hacer el movimiento de descenso y ascenso. Ciertamente, necesitamos mucha más fuerza para empujarnos de vuelta a una posición erguida. A continuación, veremos como se relaciona exactamente la fuerza con la masa y aceleración mediante argumentos matemáticos.

Proporcionalidad a la Masa
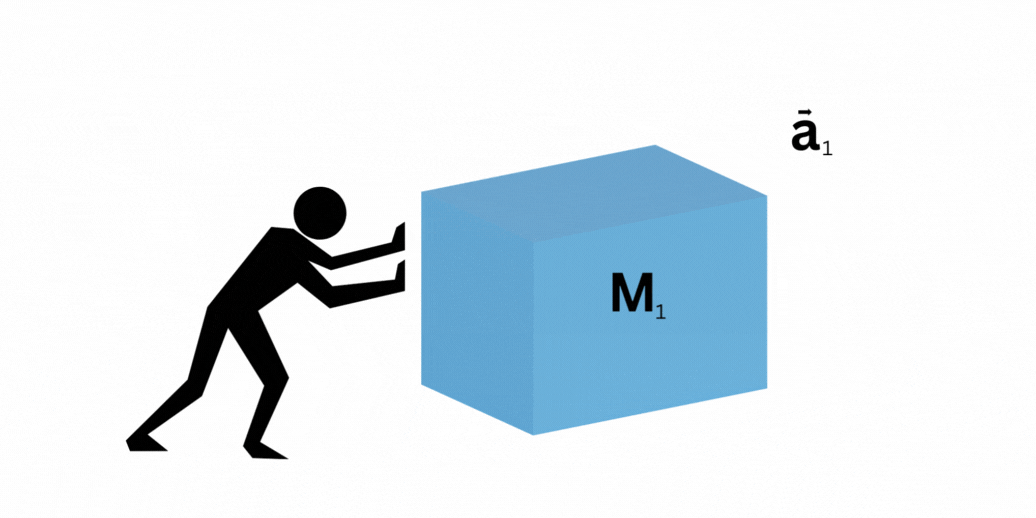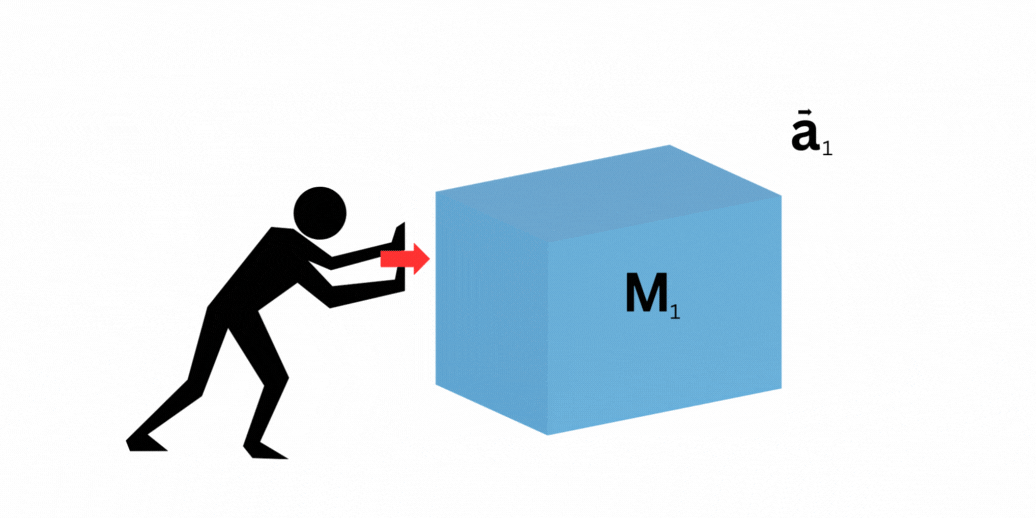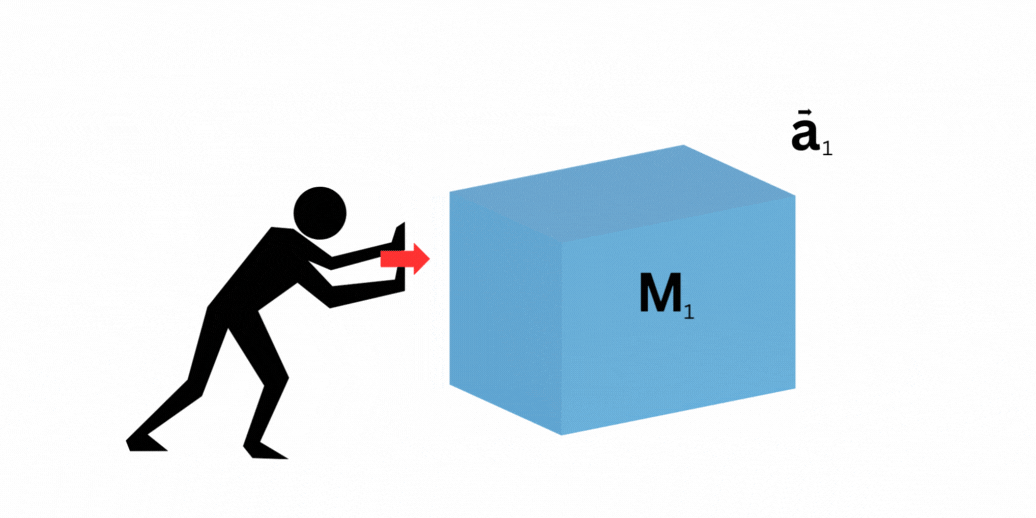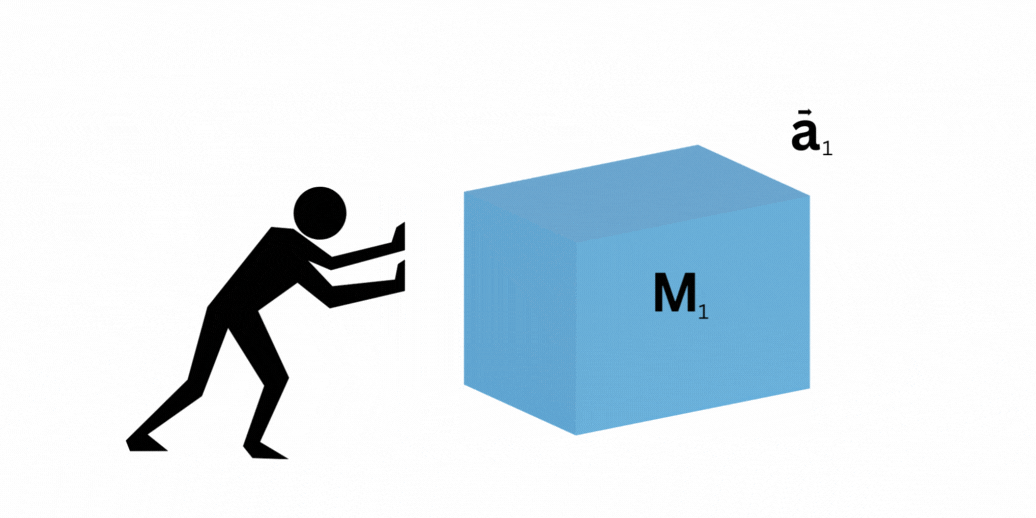
Consideremos primero una caja con masa 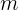 , y supongamos que necesitamos una fuerza
, y supongamos que necesitamos una fuerza 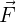 para lograr moverla. Ahora, si realizamos el mismo experimento, pero con dos cajas, cada una de masa
para lograr moverla. Ahora, si realizamos el mismo experimento, pero con dos cajas, cada una de masa 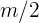 (la mitad de la caja inicial), e intentamos empujarlas, una en cada mano, necesitamos la misma cantidad de fuerza para mover ambas cajas. Es decir, la fuerza solamente depende de la masa total del sistema, y no de cada objeto. Por lo tanto, podemos concluir que la fuerza es proporcional a la masa.
(la mitad de la caja inicial), e intentamos empujarlas, una en cada mano, necesitamos la misma cantidad de fuerza para mover ambas cajas. Es decir, la fuerza solamente depende de la masa total del sistema, y no de cada objeto. Por lo tanto, podemos concluir que la fuerza es proporcional a la masa.
Proporcionalidad a la Aceleración
Más aún, podemos notar que la fuerza no es solamente proporcional a la masa, si no también a la aceleración del objeto. Esto se puede observar mediante simples experimentos:
tomemos una caja de masa 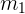 , y supongamos que le damos un fuerte impulso con ambas manos. Ahora, la caja comienza a moverse y ha experimentado una aceleración, digamos
, y supongamos que le damos un fuerte impulso con ambas manos. Ahora, la caja comienza a moverse y ha experimentado una aceleración, digamos 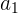 .
.
Ahora, supongamos que creamos una replica exacta de nosotros mismos, y conseguimos una segunda caja de masa 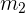 . Por simplicidad, asumiremos que
. Por simplicidad, asumiremos que 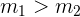 . Ahora, al mismo tiempo, con la misma intensidad, empujamos ambas cajas.
. Ahora, al mismo tiempo, con la misma intensidad, empujamos ambas cajas.
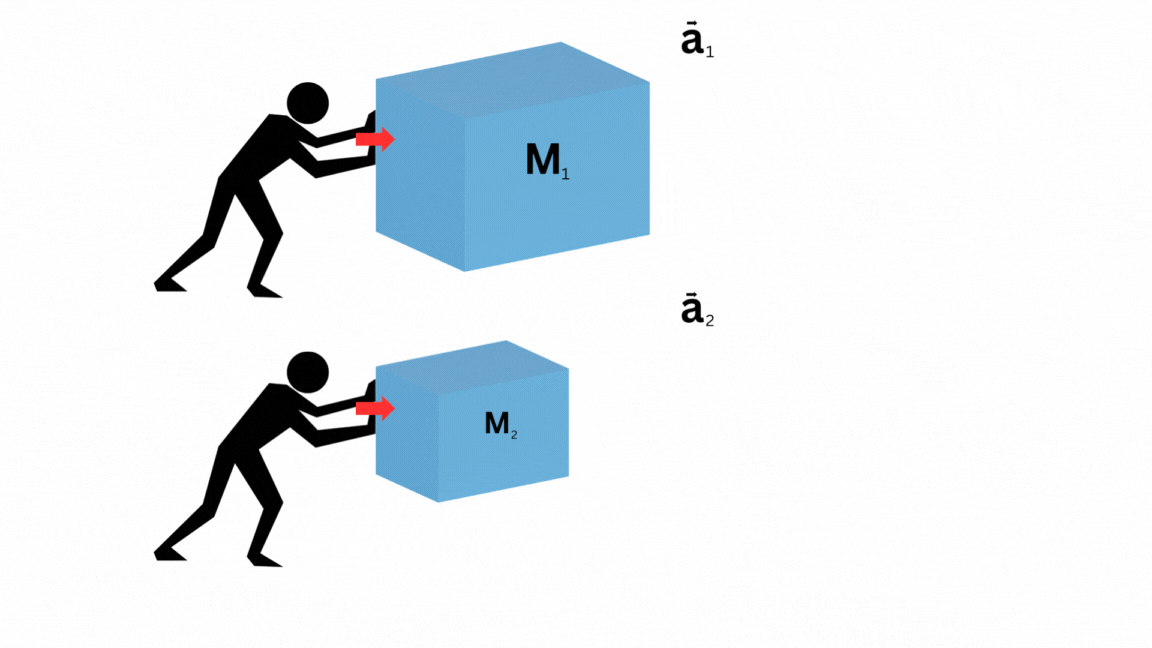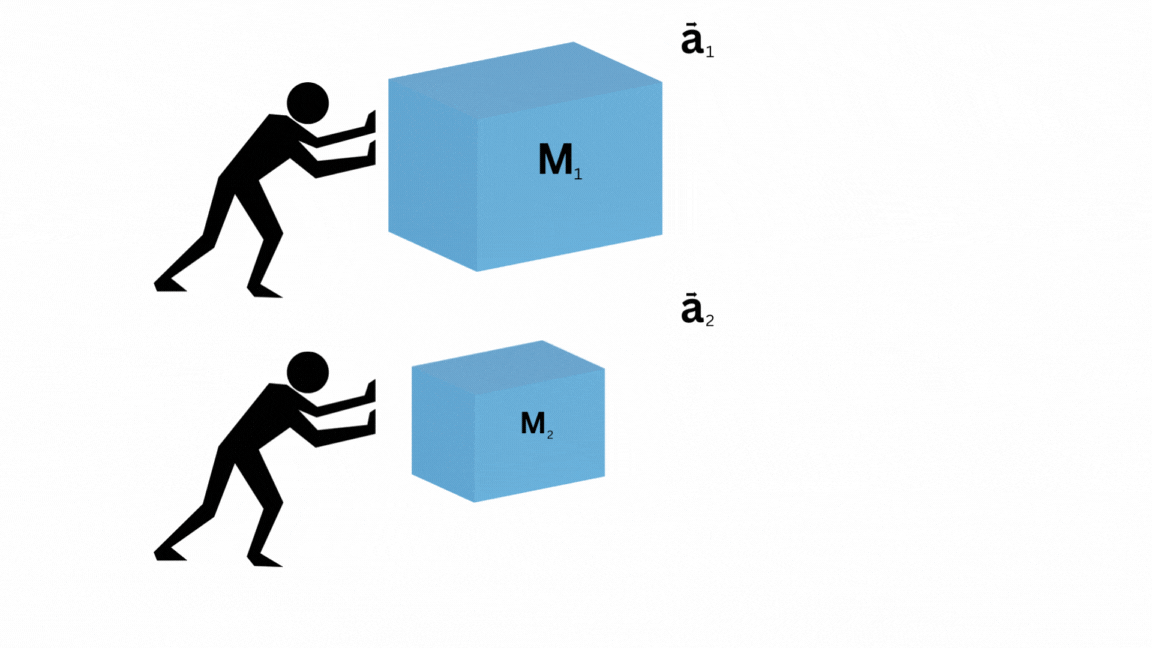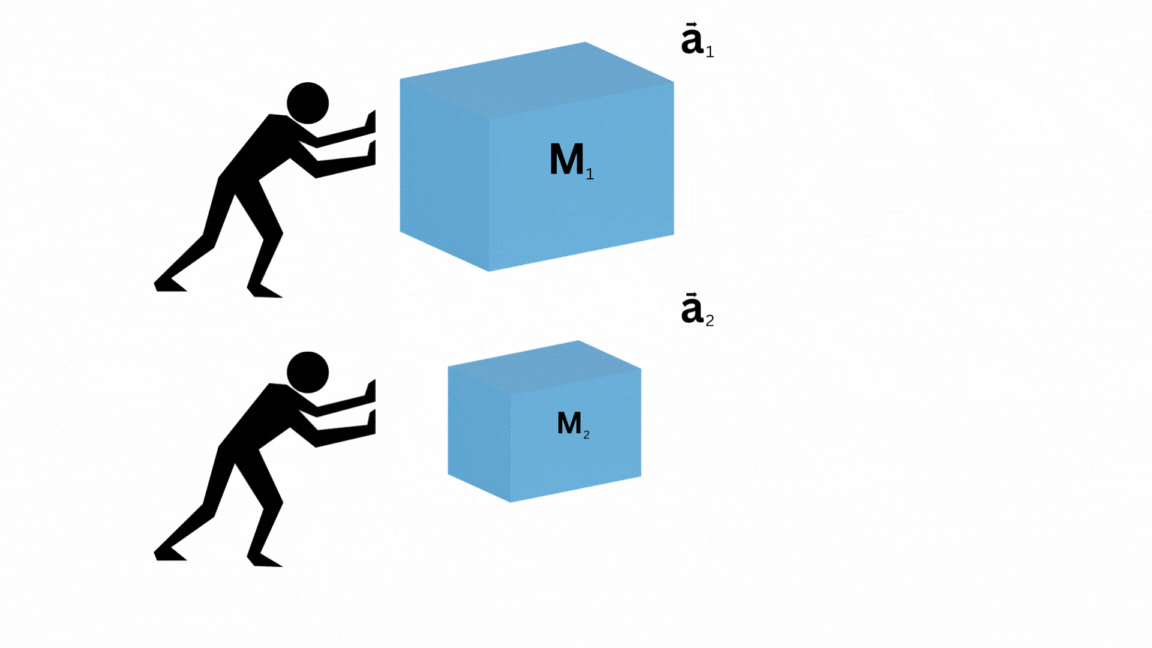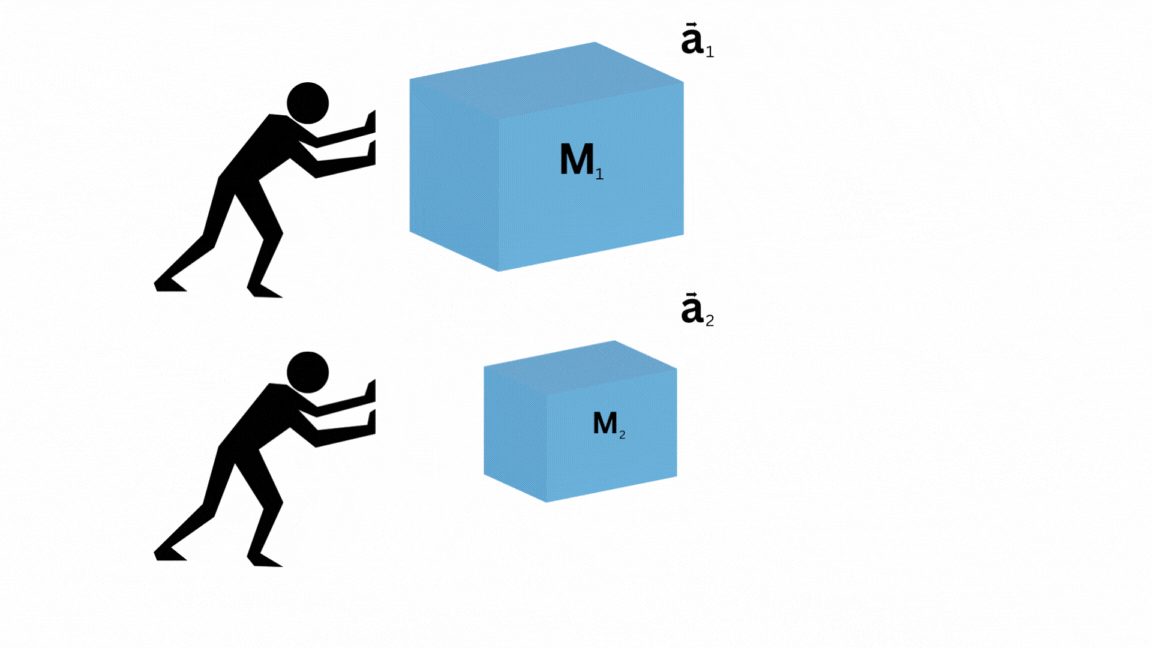
Notamos que la primer caja ha experimentado una aceleración menor a la segunda. Es decir, la fuerza ejercida ha sido proporcional a la aceleración.
Proporcionalidad Total
Con la ayuda de estos experimentos, podemos concluir que
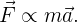
Esto es equivalente a decir que existe una constante 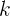 tal que
tal que
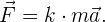
Ahora, solamente queda a nuestra elección definir lo que representa una unidad de fuerza. Para obtener la famosa fórmula de la segunda ley de Newton, definimos a 1 unidad de fuerza como aquella que se necesita para aplicarle 1 unidad de aceleración a 1 unidad de masa. Es decir,
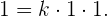
Con esto, obtenemos 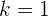 , y por lo tanto nuestra fórmula se reduce a
, y por lo tanto nuestra fórmula se reduce a
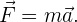
Resumir con IA:













Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.