Capítulos
La fricción es algo que podemos experimentar en todo momento. Por ejemplo, deslizando nuestro dedo sobre el móvil o la mesa. Aunque no haya mucha resistencia, esto sigue siendo fricción.
Formalmente, es la fuerza de resistencia de una superficie sólida, capas líquidas o dos materiales frotándose. Estos casos los dividimos en dos categorías:
- Fricción estática
- Fricción cinética
En este artículo, hablaremos de estos tipos de resistencia al movimiento y como afectan la dinámica de los objetos, además de su contexto matemático.
Diagramas de cuerpo libre
Antes de adentrarnos a las explicaciones de los tipos de fricción, daremos un poco de contexto de las ilustraciones que usaremos para dichas explicaciones. Los diagramas de cuerpo libre son una herramienta visual que nos ayuda a simplificar un problema donde tenemos varias fuerzas involucradas. A continuación, mostramos un ejemplo.
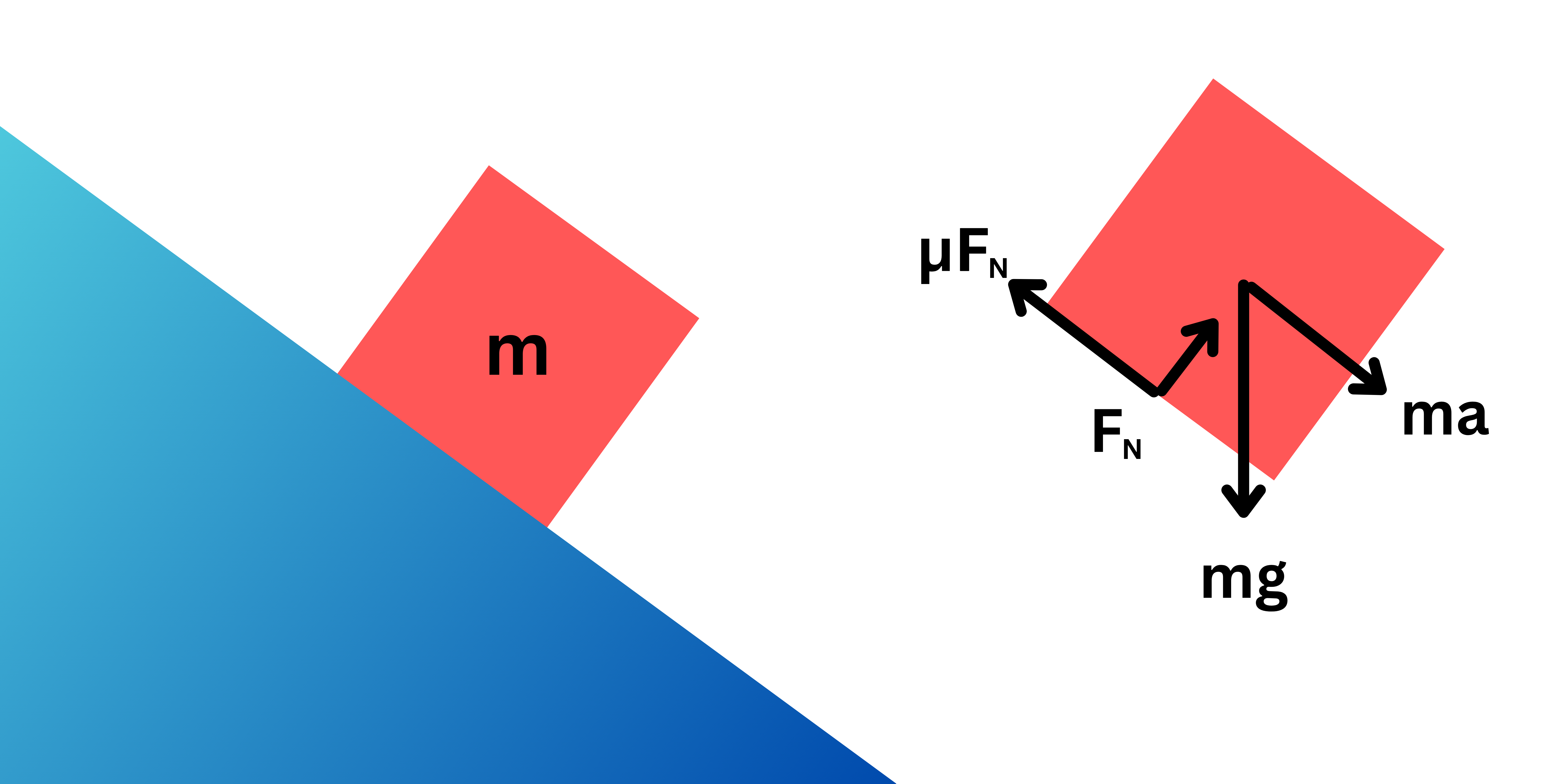
Por ahora no nos preocuparemos por los valores de cada flecha, si no del propósito de tener dicho dibujo. Con esta representación, nuestro análisis puede ser más conciso, y los cálculos necesarios que surjan al solucionar problemas serán fáciles de reconocer.
Fuerza normal
La fuerza normal se define como la fuerza neta de compresión de dos superficies paralelas. La dirección de dicha fuerza siempre es perpendicular a ambas superficies.
Coeficiente de fricción
El coeficiente de fricción, comúnmente representado por la letra griega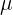 
, es un número escalar adimensional que equivale al cociente de las fuerzas de fricción de dos objetos y la fuerza de impresión entre ellos. Este coeficiente depende totalmente de los materiales, ya que, por ejemplo, deslizar un objeto sobre hielo es de mayor facilidad a deslizaros sobre el pavimento. Este número se encuentra de manera empírica, es decir, a base de experimentación.
Fricción estática
La fricción estática es aquella que ocurre entre dos o más objetos que no se mueven de manera relativa entre ellos. Por ejemplo, esta puede evitar el movimiento de un bloque que se encuentra encima de una rampa inclinada. El coeficiente de fricción estática se distingue del coeficiente de fricción cinética, donde estos se denotan por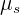 
y 
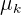, respectivamente.
Para que un objeta pueda pasar de estar estático debido a la fricción estática, este debe experimentar una fuerza externa que lo permita sobrepasar el límite de la fuerza de fricción estática. Este límite se denota por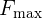 
y es igual a 
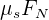, donde 
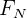denota la fuerza normal. Una vez que el objeto pase este valor, comenzará a moverse y entonces experimentarán fricción cinética.
Fricción cinética
Como se mencionó en el párrafo anterior, la fricción cinética es aquella que ocurre cuando dos objetos se frotan mientras se mueven de manera relativa entre ellos. Por ejemplo, una bola deslizándose por una colina.
La fuerza de fricción que experimentan los objetos se denota por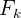 
y es igual a 
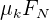. Recordemos que 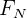denota la fuerza normal, y 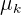representa el coeficiente de fricción cinética.
Ángulos de fricción
Un ejemplo muy común donde se estudia la fricción es en las rampas. En estos casos, tenemos que considerar el ángulo de la pendiente, y determinar si el objeto sobre dicha rampa se deslizará o no, a partir del coeficiente de fricción estático y la masa del objeto.
Supongamos que tenemos un objeto cuadrado de masa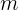 
, una rampa en forma de triángulo rectángulo con un ángulo 
. Sea 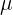el coeficiente de fricción de estos objetos. Suponiendo que ambos objetos se encuentran en el planeta Tierra, donde la gravedad 
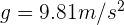, tenemos el siguiente diagrama.
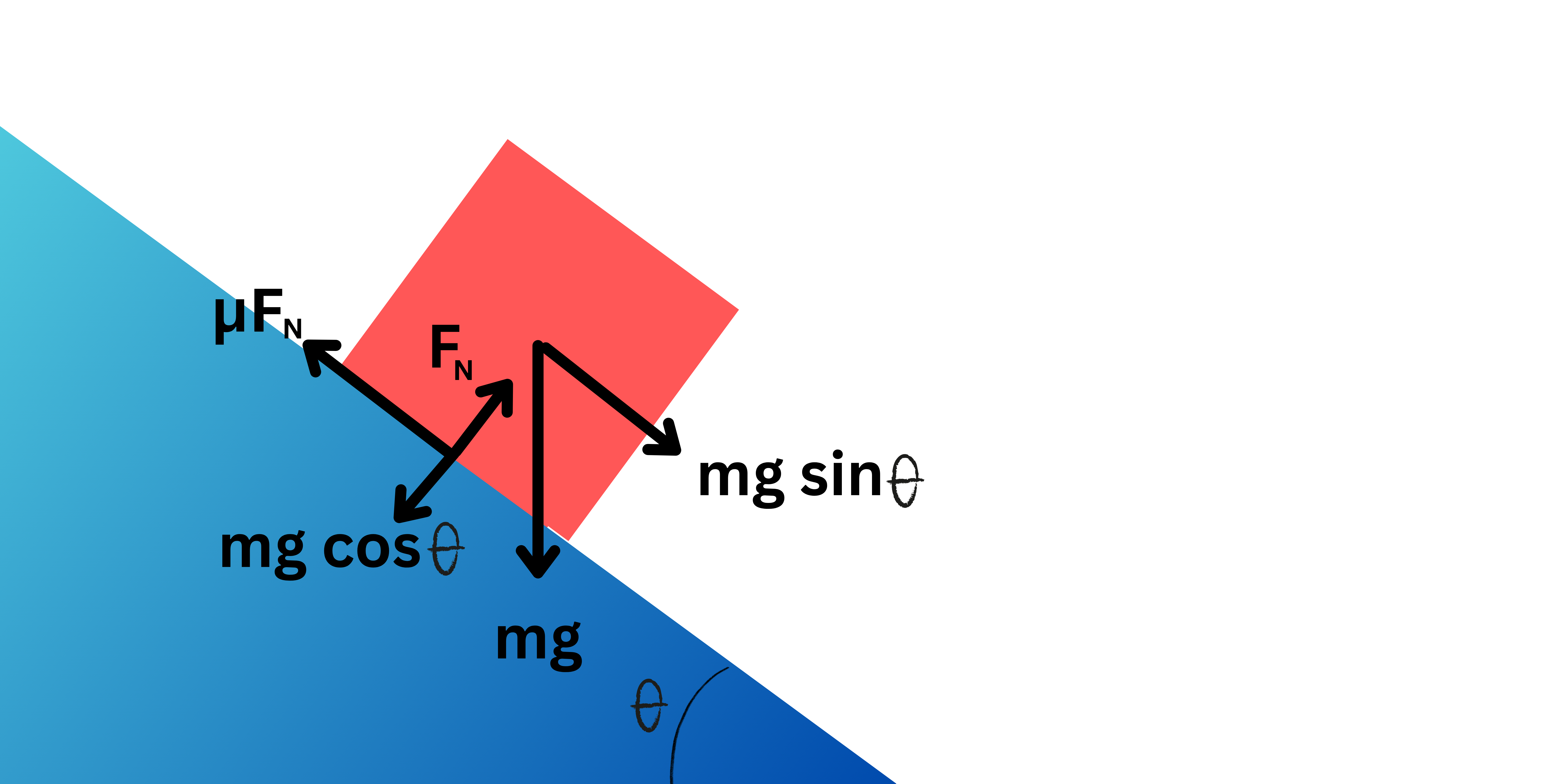
Entonces, queremos ver cuando
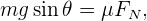
es decir, el punto en el que la fuerza que lleva la caja hacia abajo (lado izquierdo de la ecuación) es igual a la fuerza de fricción estática (lado derecho de la ecuación). De hecho, podemos hacer más con esta ecuación si recordamos que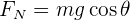 
. Tenemos entonces
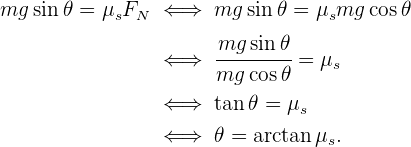
Es decir, si conocemos el coeficiente de fricción estática, podemos calcular el ángulo en el cuál el objeto comenzará a moverse. De manera inversa, podemos calcular el ángulo de fricción de manera empírica si medimos el ángulo en el cual el objeto se comienza a deslizar por la rampa. Cabe mencionar que en los cálculos anteriores no dependen de la gravedad ni la masa del objeto. Entonces, podemos llegar a la misma conclusión en cualquier otro planeta, y con cualquier cantidad de masa.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.