Capítulos
La dinámica, rama fundamental de la física que estudia el movimiento de los objetos y las fuerzas que los afectan, se adentra en conceptos cruciales para comprender la naturaleza del movimiento. Entre estos conceptos, el momento desempeña un papel crucial, tanto en su forma lineal como angular.
Momento Lineal
Una partícula
El momento lineal es una magnitud vectorial que describe el movimiento de un objeto. Se define como el producto de la masa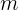 
del objeto multiplicada por 
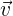, la velocidad del objeto, que denotamos como 
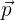para obtener
Esto quiere decir que las dimensiones del momento son
Para comprender este concepto,
recordemos la Segunda Ley de Newton, que describe que la tasa de cambio de momento de un objeto es proporcional a la fuerza actuando sobre él.
Varias partículas
Si tenemos un sistema de diversas partículas, debemos considerar la masa y momento de cada una de ellas. Si tenemos 2,
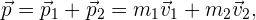
donde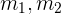 
son las masas, 
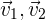las velocidades de cada objeto, respectivamente. En general, tenemos
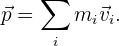
Conservación
En sistemas cerrados (donde no interfieren objetos ni fuerzas externas), el momento se mantiene constante. Conocida como la ley de conservación de momento, se puede deducir por las Leyes de Newton. Para ver esto, tomemos 2 partículas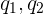 
y las hacemos interactuar. Por la tercera ley, las fuerzas ejercidas entre estos objetos son iguales en magnitud pero en direcciones contrarias. La segunda ley nos dice que el cambio de momento es igual a la fuerza, por lo que
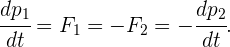
De manera equivalente,
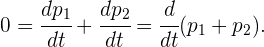
Es decir, la suma de momentos es constante.
Momento Angular
En 2 dimensiones
El momento angular representa el producto de la inercia rotacional y velocidad rotacional. Es decir, la cantidad de fuerza necesaria para generar aceleración angular, y el cambio de posición angular en el tiempo, con respecto a un eje. Si el movimiento solo ocurre en un plano, podemos considerar el momento angular como un análogo al momento lineal, donde el momento lineal es
y el momento angular 
es proporcional al momento de inercia 
y velocidad angular 
, medida en radianes por segundo. Es decir,
A diferencia de la masa en el momento lineal, el momento de inercia depende de su posición con respecto al eje de rotación. Asimismo, la velocidad angular depende del centro del cual se orbita.
Si el movimiento es completamente circular, podemos simplificar nuestra ecuación a
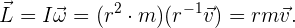
Momento angular en 3 dimensiones
Definimos el momento angular como
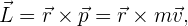
donde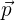 
es el momento lineal de la partícula y 
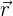al vector radial del origen del movimiento hacia la partícula. Recordemos que el producto cruz nos genera un vector perpendicular al plano donde se encuentran los vectores 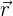y .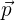
Cambio en el Momento Angular
Recordemos que en el caso del momento lineal, teníamos que la tasa de cambio del momento lineal era igual a la fuerza. Ahora, veremos que para el momento angular, ocurre algo similar. Al derivar la expresión del momento angular:
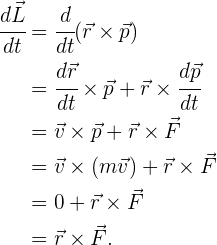
Es decir, el cambio en el momento angular es perpendicular a la fuerza y al vector radial.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.