Capítulos
Las tres leyes de Newton son tres principios o enunciados que explican una gran parte de los problemas relacionados al movimiento de ciertos objetos. Es decir, éstas pueden explicar desde el movimiento de los planetas y otros astros, hasta la trayectoria de una simple bola de béisbol. A continuación, veremos detalladamente cada una de ellas.

Primera Ley
La primer ley, también conocida como la ley de inercia, establece que un cuerpo en movimiento se mantiene en movimiento a no ser por fuerzas externas. Es decir, si un cuerpo está en movimiento y no hay un tercero que le intente aplicar una fuerza, este no se detendrá. De manera análoga, un objeto en reposo se mantendrá en reposo si no se le aplica una fuerza ajena.
Esto nos dice, entonces, que cualquier objeto suficientemente cerca del planeta tierra está constantemente recibiendo una fuerza externa. Por ejemplo, la luna que nos orbita. Esto es, si repentinamente la tierra deja de ejercer una fuerza sobre la luna, ésta saldría disparada. Algo similar ocurre en el lanzamiento de martillo, como se puede observar en el siguiente video.
Mientras la bola no sea soltada, no saldrá disparada. Durante todo momento, observamos que la fuerza gravitacional de la tierra no permite que la bola siga en movimiento (es decir, que siga volando al ser soltada).
En términos matemáticos, lo que concluimos de éstas observaciones es que
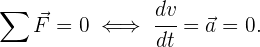
En palabras, que la suma de las fuerzas  aplicadas sobre un objeto son 0 si, y solo si, el objeto no experimenta aceleración.
aplicadas sobre un objeto son 0 si, y solo si, el objeto no experimenta aceleración.
Segunda Ley
La segunda ley de Newton, también conocida como la ley fundamental de la dinámica, establece que el cambio de momento (en ese entonces Newton usaba la palabra "movimiento") de un objeto es directamente proporcional a la fuerza impresa sobre éste, en la dirección en la cual dicha fuerza ha sido aplicada.
El momento de un objeto es definido como la multiplicación escalar de la masa del objeto por su vector de velocidad. Es decir, si denotamos al momento del objeto como 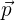 , su masa como
, su masa como 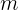 y su velocidad como
y su velocidad como  , podemos escribir
, podemos escribir
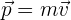
De esta manera, la segunda ley de Newton nos dice que la fuerza es la derivada (el cambio) del momento del objeto, por lo que obtenemos
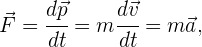
donde  denota la aceleración del objeto.
denota la aceleración del objeto.
En términos de la posición del objeto, esta misma ecuación puede ser reescrita como
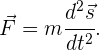
Cabe destacar que cuando actúan varias fuerzas sobre el mismo objeto, la segunda ley de Newton nos habla precisamente de la fuerza resultante, que se define como la suma vectorial de cada fuerza independiente aplicada sobre el objeto. Es decir, si sobre el objeto se aplican 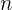 fuerzas denotadas por
fuerzas denotadas por 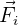 para
para 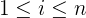 , entonces
, entonces
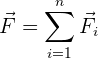
es la fuerza resultante.
Unas aplicaciones de la segunda ley de Newton incluyen el cálculo de la caída libre de un objeto, el movimiento de un péndulo simple o un resorte simple.
Tercera Ley
La tercera ley de Newton, también conocida como el principio de acción y reacción, describe lo que experimentamos si intentamos empujar una pared (con buenos cimientos) con toda la fuerza que poseemos: no logra moverse. Adicionalmente, sentimos como la pared nos aplica una fuerza sobre nuestro cuerpo a pesar de ser nosotros quienes la empuja. Es decir, a cada acción ocurre una reacción contraria. Cuando intentamos empujar la pared, la pared nos empuja de vuelta, con la misma fuerza que aplicamos.

Esta ley viene de un concepto más fundamental: la conservación de momento. En este contexto, nos dice que si tenemos dos objetos con momentos 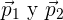 respectivamente, entonces el momento total del sistema es de
respectivamente, entonces el momento total del sistema es de 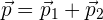 . Por la segunda ley de Newton, sabemos que la derivada (la tasa de cambio con respecto al tiempo) del momento es precisamente la fuerza. Entonces,
. Por la segunda ley de Newton, sabemos que la derivada (la tasa de cambio con respecto al tiempo) del momento es precisamente la fuerza. Entonces,
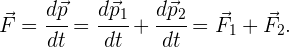
Suponiendo que no hay más fuerzas involucradas, la tercera ley de Newton nos dice que 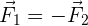 .
.
Resumir con IA:













Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.