Los ejercicios que encontrarás a continuación te permitirán aplicar y consolidar tus conocimientos sobre diagramas de espacio-tiempo. Prepárate para poner en práctica tus habilidades, ya que cada ejercicio te desafiará a aplicar diagramas y fórmulas específicos.
El diagrama espacio-tiempo correspondiente a un cuerpo en reposo, donde el eje espacial es el horizontal, es...
Selecciona una respuesta.
1 Consideramos el eje horizontal como el eje espacial 
y el vertical como el eje temporal 
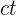, donde 
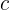representa la velocidad de la luz
2Para graficar un objeto en reposo, se requiere que su coordenada espacial sea la misma para cualquier punto de la gráfica; así, un objeto en reposo se representa con una recta vertical.
El diagrama espacio-tiempo correspondiente a un cuerpo con movimiento rectilíneo uniforme, donde el eje espacial es el horizontal, es...
Selecciona una respuesta.
Se sigue de la gráfica de la posición respecto al tiempo de un objeto con movimiento rectilíneo uniforme.
Para un objeto con movimiento rectilíneo uniforme, el ángulo entre la recta y el eje temporal es...
Selecciona una respuesta.
1 Consideramos el eje horizontal como el eje espacial y el vertical como el eje temporal 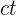, donde 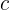representa la velocidad de la luz
2Para graficar un objeto con movimiento recilíneo, basta recordar que la velocidad es la pendiente de gráfica de la posición respecto al tiempo.
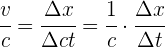
3Como el eje espacial es el horizontal,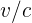 
es el ángulo comprendido entre la recta y el eje temporal.
Si la velocidad de un objeto con movimiento rectilíneo uniforme es pequeña, entonces la recta en el diagrama espacio-tiempo tiende a ser...
Selecciona una respuesta.
1 Consideramos el eje horizontal como el eje espacial y el vertical como el eje temporal 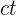, donde 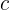representa la velocidad de la luz
2Para graficar un objeto con movimiento recilíneo, basta recordar que la velocidad es la pendiente de gráfica de la posición respecto al tiempo.
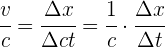
3Como el eje espacial es el horizontal, 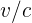es el ángulo comprendido entre la recta y el eje temporal. Así, si la velocidad es pequeña, entonces la recta se aproxima a la vertical
El intervalo de tiempo entre los acontecimientos A(2,1), B(7,4) en el sistema de referencia en que ambos transcurren en un mismo punto es...
Selecciona una respuesta.
1 Expresamos los puntos en el diagrama espacio-tiempo
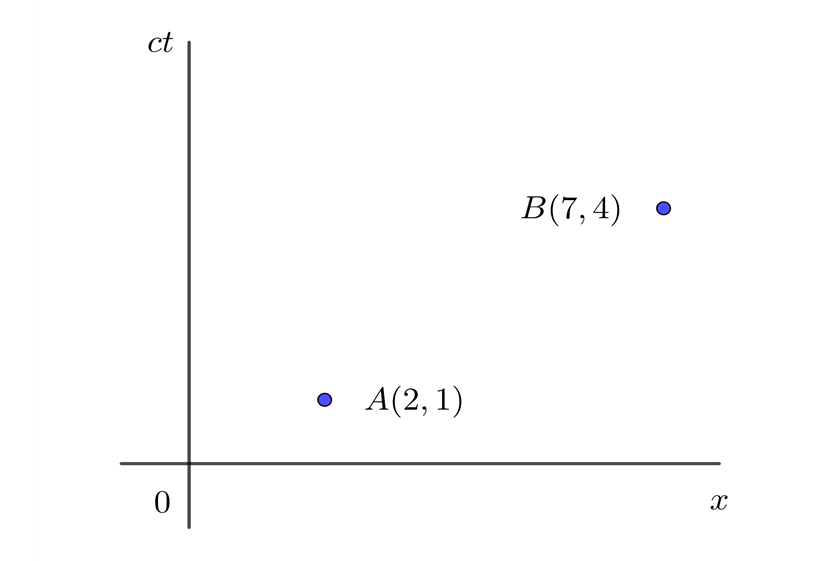
2 Podriamos pensar que podemos calcular el tiempo empleando Pitágoras, pero Pitágoras es válido en espacios Euclideanos y los diagramas de espacio-tiempo son espacios de Minkowski por lo que debemos aplicar
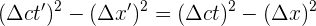
3Como el sistema de referencia transcurre en un mismo punto,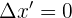 
. Sustituyendo se obtiene
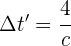
El intervalo de tiempo entre los acontecimientos A(2,1), B(5,6) en el sistema de referencia en que ambos son simultáneos es...
Selecciona una respuesta.
1 Expresamos los puntos en el diagrama espacio-tiempo
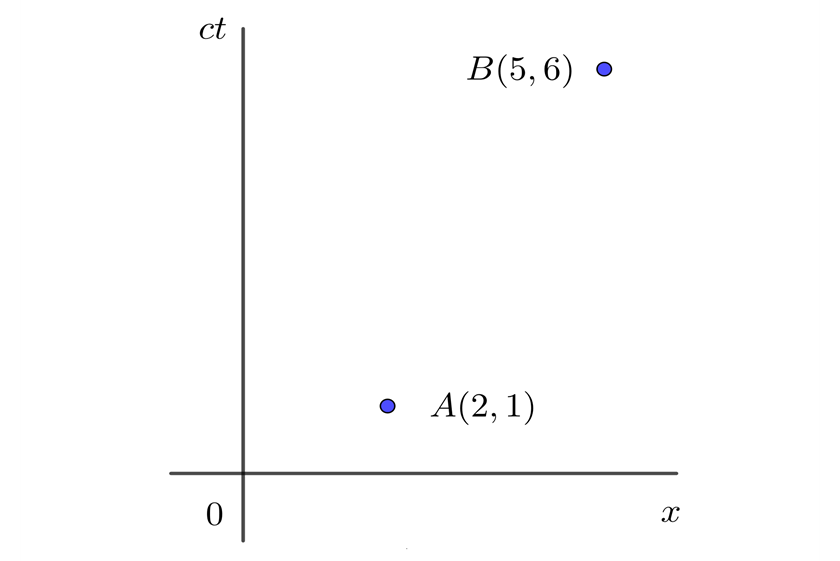
2 Podriamos pensar que podemos calcular la distancia empleando Pitágoras, pero Pitágoras es válido en espacios Euclideanos y los diagramas de espacio-tiempo son espacios de Minkowski por lo que debemos aplicar
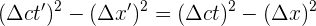
3Como en el sistema de referencia ambos son simultáneos,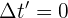 
. Sustituyendo se obtiene
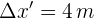
Un pasajero de un tren se encuentra en el punto medio de un vagón y enciende una linterna de manera que la luz se propaga hacia las puertas trasera y delantera. Si para el pasajero el diagrama espacio-tiempo es simultáneo, entonces para el observador en el andén el diagrama espacio-tiempo es...
Selecciona una respuesta.
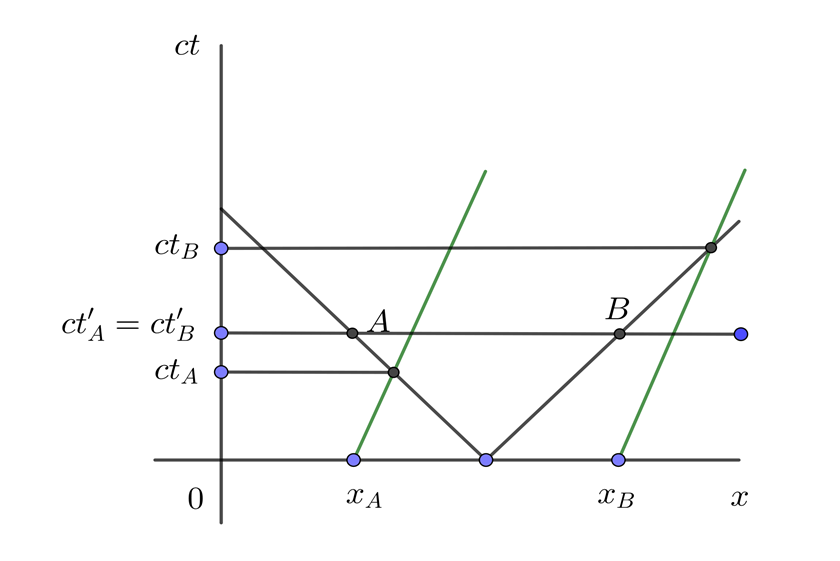
1 Expresamos los puntos en el diagrama espacio-tiempo para el pasajero del tren y notamos que A y B son simultáneos en S'
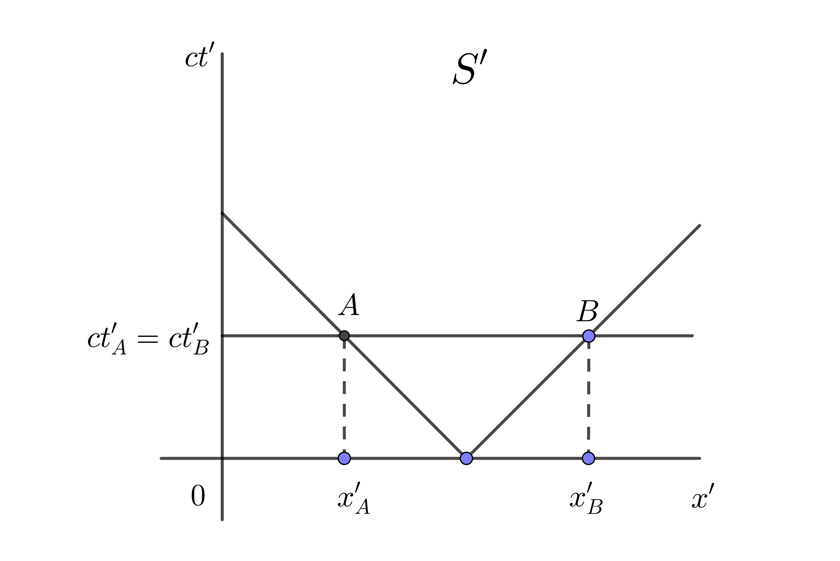
2 Expresamos los puntos en el diagrama espacio-tiempo para el observador en el andén y notamos que A y B no son simultáneos en S
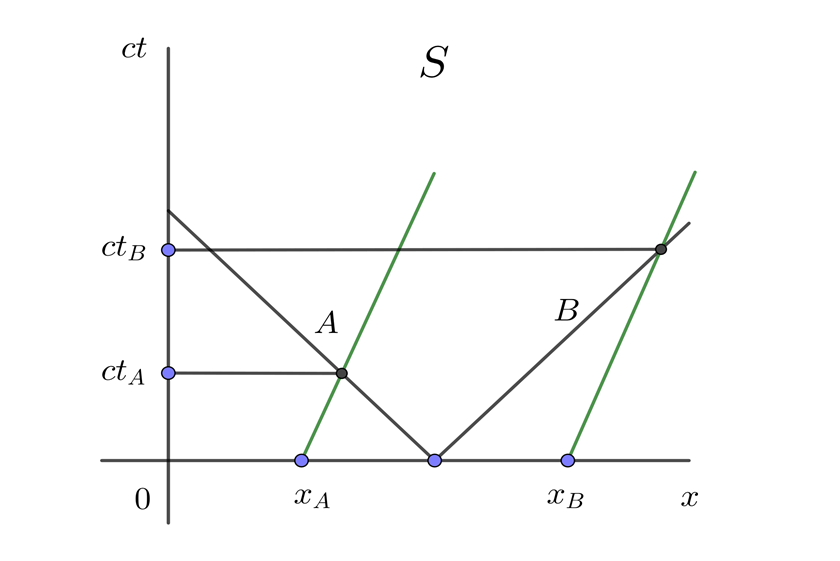
3 Expresamos S y S' en el diagrama espacio-tiempo
Un piloto viaja en una nave espacial con velocidad de 0.65c. Al pasar por la Tierra su reloj es ajustado a las 10:00 am. Poco después pasa por una estación fija con respecto a la tierra, vuelve a observar su reloj y este marca las 10:40 am. La hora en la estación al pasar la nave es...
Selecciona una respuesta.
1La hora en la estación debe ser mayor que la marcada por el reloj del piloto, esto debido a la dilatación del tiempo.
2 Indicamos los datos conocidos
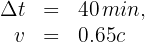
3 Empleamos la fórmula de dilatación del tiempo
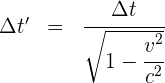
4Sustituimos los datos conocidos en la fórmula de dilatación del tiempo
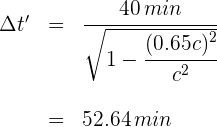
5En la estación espacial son las 10:52.64 am
Un observador en reposo tiene una barra de 4.3 metros y un observador en movimiento con una velocidad de 0.00005c observa la barra pasar frente a él. La medida de la barra observada por la persona en movimiento es...
Selecciona una respuesta.
1La medida de la barra vista por el observador en movimiento es menor respecto a la medida observada por la persona en reposo, esto debido a la contracción de espacio.
2 Indicamos los datos conocidos
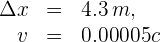
3 Empleamos la fórmula de contracción del espacio
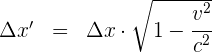
4Sustituimos los datos conocidos en la fórmula de contracción del espacio
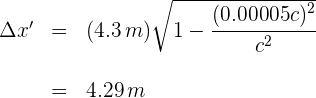
5El observador en movimiento midió 4.29 m por la barra.
Un observador determina que dos eventos están separados por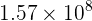 
metros y que ocurre con una separación de 3 segundos. El intervalo propio entre ambos es...
Selecciona una respuesta.
1Consideramos un segundo observador en movimiento respecto al primero y que determina que los dos eventos ocurren en la misma localización espacial. El intervalo propio entre ambos eventos es el medido por el observador en movimiento.
2 Indicamos los datos conocidos
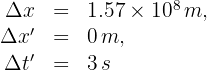
3 Empleamos la fórmula de Lorentz
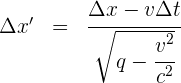
4Sustituyendo los datos se obtiene
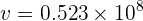
de donde se obtiene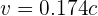 
.
5 Empleamos la fórmula de dilatación del tiempo
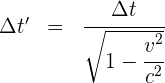
4Sustituimos los datos conocidos en la fórmula de dilatación del tiempo
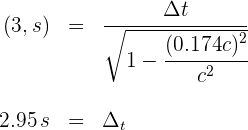
Si tienes dudas puedes consultar ejercicios resueltos del tema.
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Muy importante saber las fórmulas y rl conceptos de cada teoría ya que de ellos depende hacer bien las fórmulas
Hola, no entiendo el problema 10 de Problemas resueltos de diagramas espacio-tiempo, me lo podrían explicar mas detalladamente por favor.
Hola si te refieres a la parte de calcular la velocidad de la fórmula [latex]\Delta x’=\frac\Delta x-v\Delta t\sqrtq-\fracv^2c^2[/latex] tendrías que sustituir los datos y te quedaria una ecuación de segundo grado y resolverla con fórmula general.
Como en el ejercicio 6 y 7 resuelve el sistema t1 t2
Hola, el sistema se puede resolver con el método de sustitución, se despeja t1 de la primera ecuación y el resultado se sustituye en la segunda ecuación y como solo queda como variable t2 esta se despeja y después el resultado se sustituye para calcular t1.
La fuerza normal como esta perpendicular a la superfeficie pertenece al eje Y, entonce no seria cos en ves del seno? es el ejercicio 4 qu elo saca con el seno y deberia ser con el coseno o no se si me equivoco
v¹= 1500 m/sy v²=4500 m/s?
Hola esa pregunta que haces es muy importante pues causa mucha confusión, en realidad debe usarse el seno en vez del coseno ya que el ángulo agudo se forma después de los 180 grados y construyendo un triangulo rectángulo el cateto opuesto queda en el eje y lo que implicaría usar la función seno.
Problema no.9 grados 40 en procedimiento 50??
Hola no sé qué artículo te refieres pues revise y no encontre el ejercicio 9 con los datos mencionados.