Los sistemas de ecuaciones logarítmicas están formados por dos o más ecuaciones que contienen logaritmos de expresiones algebraicas. Este tipo de sistemas aparece frecuentemente en problemas relacionados con escalas logarítmicas (como la escala de Richter, el pH, o la intensidad del sonido), así como en contextos donde se desea invertir procesos exponenciales.
Además, es importante tener en cuenta las restricciones del dominio: solo se pueden aplicar logaritmos a números positivos, por lo que es necesario verificar que las soluciones obtenidas sean válidas dentro del contexto del problema.
En esta sección encontrarás ejercicios resueltos paso a paso que te permitirán practicar la resolución de sistemas logarítmicos con distintos niveles de dificultad. Aprenderás a simplificar expresiones logarítmicas, a aplicar correctamente las propiedades, y a resolver ecuaciones resultantes mediante sustitución, igualación o transformación algebraica.
Resuelve los siguientes sistemas de ecuaciones
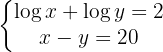
En la primera ecuación aplicamos la propiedad del logaritmo de un producto.
Aplicamos la inyectividad de los logaritmos y despejamos la 
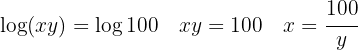
Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
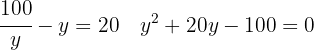
Resolvemos la ecuación de 2º grado, con la formula general 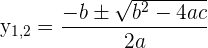
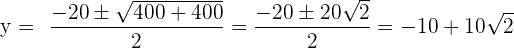

Ahora calculamos el valor de

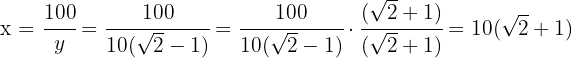
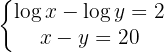
En la primera ecuación aplicamos la propiedad del logaritmo de un cociente.
Aplicamos la inyectividad de los logaritmos y despejamos la 
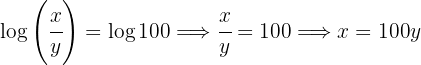
Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
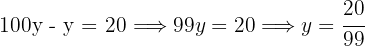
Ahora calculamos el valor de 
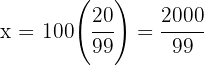
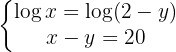
Aplicamos la inyectividad de los logaritmos y despejamos la 
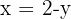
Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
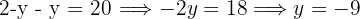
Ahora calculamos el valor de 
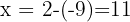
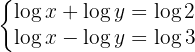
En la primera ecuación aplicamos la propiedad del logaritmo de un producto y la de un cociente en la segunda.
Aplicamos la inyectividad de los logaritmos y despejamos la 
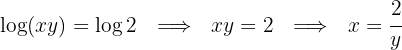
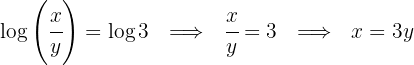
Igualamos ambos valores de 
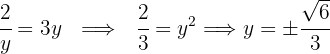
Ahora calculamos el valor de 
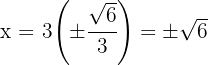
La solución son los elementos positivos 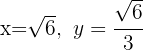
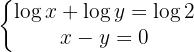
En la primera ecuación aplicamos la propiedad del logaritmo de un producto.
Aplicamos la inyectividad de los logaritmos y despejamos la 
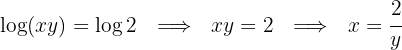
Despejamos  en la segunda ecuación
en la segunda ecuación
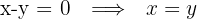
Igualamos ambos valores de 
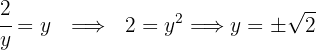
Ahora calculamos el valor de 
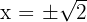
La solución son los elementos positivos 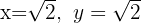
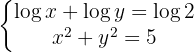
En la primera ecuación aplicamos la propiedad del logaritmo de un producto.
Aplicamos la inyectividad de los logaritmos y despejamos la 
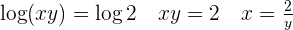
Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
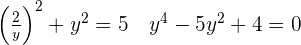
Resolvemos la ecuación de 2º grado, con la formula general 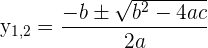
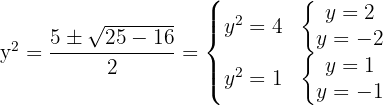
Encontramos las soluciones para las
 positivas
positivas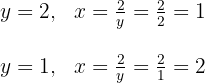
Si sustituimos las
 negativas en la ecuación nos encontramos con el logaritmo de un número negativo, el cual no está bien definido.
negativas en la ecuación nos encontramos con el logaritmo de un número negativo, el cual no está bien definido.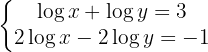
Resolvemos el sistema por reducción multiplicando la primera ecuación por 
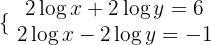
Aplicamos la definición de logaritmo para despejar la 
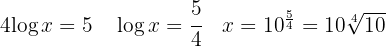
Sustituimos el valor de 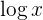 en la primera ecuación.
en la primera ecuación.
Aplicamos la definición de logaritmo para despejar la 
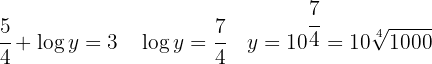
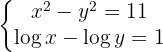
En la segunda ecuación aplicamos la propiedad del cociente de un logaritmo, en el primer miembro y en segundo tenemos en cuenta que el logaritmo decimal de  es
es  .
.
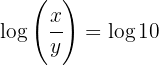
Resolvemos el sistema por sustitución
Aplicamos la inyectividad de los logaritmos
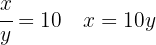
Sustituimos en la primera ecuación
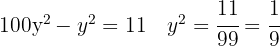
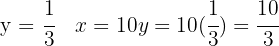
La solución 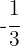 no es válida porque tendríamos el logaritmo de un número negativo en la segunda ecuación
no es válida porque tendríamos el logaritmo de un número negativo en la segunda ecuación
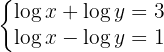
Resolvemos el sistema por reducción
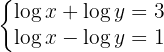
Aplicamos la definición de logaritmo

Sustituimos en la otra ecuación

Aplicamos la definición de logaritmo
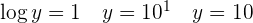
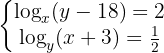
Aplicamos la definición de logaritmo en las dos ecuaciones
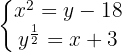
Elevamos al cuadrado en los dos miembros de la segunda ecuación y sustituimos el valor de  en la primera ecuación
en la primera ecuación

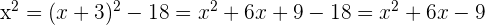
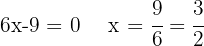
Operamos y resolvemos la ecuación
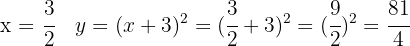
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Por favor corrija la propiedad 7
Hola podrías mencionar cual es el error de la propiedad 7 o es un ejercicio?
Como resuelvo el cálculo log4(x)+log3(x-2)=1
Necesito resolver estos ejercicios.aplica las propiedades logarítmicas las siguientes expresiones.a)log4(2/6) b)log4(4.5)
310=902,5/8,69ª
Quiero despejar a de allí
Es unpoco largo, es confuso vuando pone laprimera definicion logaX=Y, y dice que X es la ingonita. log aY=X lo expresa mejor
Hola agradecemos tu comentario pues nos ayuda a ser mas claros al explicar, vamos a analizar tu sugerencia para hacer los cambios necesarios.
-6(-×+3)/2