Los sistemas de ecuaciones exponenciales están formados por dos o más ecuaciones en las que las variables aparecen en los exponentes. Estos sistemas son comunes en el modelado de fenómenos de crecimiento o decrecimiento, como el interés compuesto, la desintegración radiactiva, el crecimiento poblacional y otros procesos naturales o económicos.
A continuación se presentan ejercicios resueltos paso a paso que te ayudarán a identificar el mejor método para resolver diferentes tipos de sistemas exponenciales. A través de la práctica, podrás fortalecer tus habilidades en la resolución de ecuaciones no lineales y comprender mejor el comportamiento de funciones exponenciales en contexto.
Resuelve los siguientes sistemas de ecuaciones:
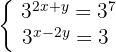
1 Reconocimiento de los exponentes y sus bases
Puesto que en ambos miembros de la igualdad las potencias son de la misma base, se igualan los exponentes correspondientes y se resuelve el sistema  . Recuerda que si el exponente es
. Recuerda que si el exponente es  no suele escribirse como potencia.
no suele escribirse como potencia.
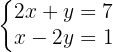
2 Aplicación del método de sustracción para resolver el sistema de 
Multiplicando por  la primera ecuación del sistema
la primera ecuación del sistema

y sumando ambas ecuaciones término a término, se tiene que:
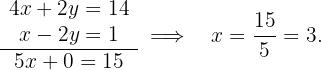
Sustituyendo el valor de  en cualquiera de las dos literales se obtiene el valor de
en cualquiera de las dos literales se obtiene el valor de  :
:
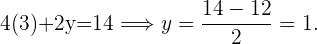
Por tanto, la solución del sistema es 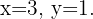
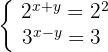
1 Reconocimiento de los exponentes y sus bases
En la primera ecuación se tiene la misma base, por lo que al igualar los exponentes se obtiene
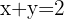
En la segunda ecuación se tiene la misma base, por lo que al igualar los exponentes se obtiene
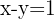
Se obtiene el sistema de ecuaciones
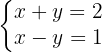
2 Aplicación del método de sustracción para resolver el sistema de 
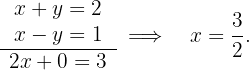
Sustituyendo el valor de  en cualquiera de las dos literales se obtiene el valor de
en cualquiera de las dos literales se obtiene el valor de  :
:
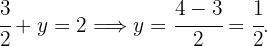
Por tanto, la solución del sistema es 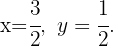
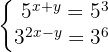
1 Reconocimiento de los exponentes y sus bases
En la primera ecuación se tiene la misma base, por lo que al igualar los exponentes se obtiene
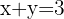
En la segunda ecuación se tiene la misma base, por lo que al igualar los exponentes se obtiene
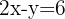
Se obtiene el sistema de ecuaciones
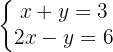
2 Aplicación del método de sustracción para resolver el sistema de 
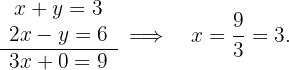
Sustituyendo el valor de  en cualquiera de las dos literales se obtiene el valor de
en cualquiera de las dos literales se obtiene el valor de  :
:

Por tanto, la solución del sistema es 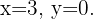
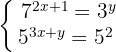
1 Reconocimiento de los exponentes y sus bases
En la primera ecuación se tiene la misma base, por lo que al igualar los exponentes se obtiene

En la segunda ecuación se tiene la misma base, por lo que al igualar los exponentes se obtiene
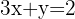
Se obtiene el sistema de ecuaciones
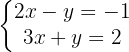
2 Aplicación del método de sustracción para resolver el sistema de 
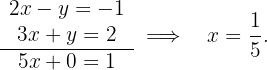
Sustituyendo el valor de  en cualquiera de las dos literales se obtiene el valor de
en cualquiera de las dos literales se obtiene el valor de  :
:
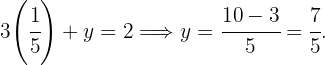
Por tanto, la solución del sistema es 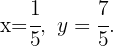
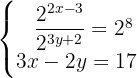
1 Reconocimiento de los exponentes y sus bases
Primero se aplica la división de una potencia al primer miembro de la primera ecuación para obtener una potencia de misma base en toda la ecuación:

Ahora, los exponentes de la primera ecuación se igualan porque sus potencias tienen la misma base y se reduce la ecuación:

así, se considera la segunda ecuación para formar el sistema  y se resuelve.
y se resuelve.
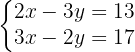
2 Aplicación del método de sustracción para resolver el sistema de 
Se multiplica por  la primera ecuación del sistema y por
la primera ecuación del sistema y por  la segunda ecuación
la segunda ecuación
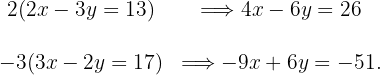
Ambas ecuaciones se suman término a término y se halla el valor de  :
:
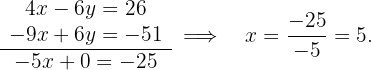
Posteriormente, se sustituye el valor de  en alguna de las dos ecuaciones del sistema y se calcula
en alguna de las dos ecuaciones del sistema y se calcula  :
:

Por tanto, la solución del sistema es 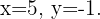
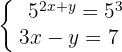
1 Los exponentes de la primera ecuación se igualan porque sus potencias tienen la misma base y se reduce la ecuación:
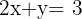
así, se considera la segunda ecuación para formar el sistema  y se resuelve.
y se resuelve.
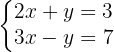
2 Aplicación del método de sustracción para resolver el sistema de 
Ambas ecuaciones se suman término a término y se halla el valor de  :
:
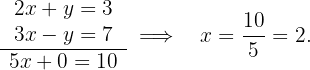
Posteriormente, se sustituye el valor de  en alguna de las dos ecuaciones del sistema y se calcula
en alguna de las dos ecuaciones del sistema y se calcula  :
:
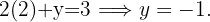
Por tanto, la solución del sistema es 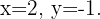
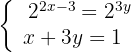
1 Los exponentes de la primera ecuación se igualan porque sus potencias tienen la misma base y se reduce la ecuación:
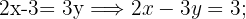
así, se considera la segunda ecuación para formar el sistema  y se resuelve.
y se resuelve.
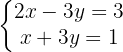
2 Aplicación del método de sustracción para resolver el sistema de 
Ambas ecuaciones se suman término a término y se halla el valor de  :
:
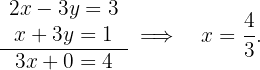
Posteriormente, se sustituye el valor de  en alguna de las dos ecuaciones del sistema y se calcula
en alguna de las dos ecuaciones del sistema y se calcula  :
:
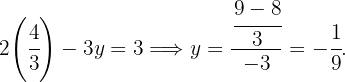
Por tanto, la solución del sistema es 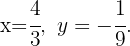
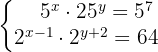
1 Reconocimiento de los exponentes y sus bases
En la primera ecuación se aplica el producto de potencias para simplificar el primer miembro y poder igualar sus exponentes
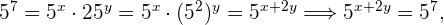
y para la segunda ecuación se utilizan las propiedades del producto y del cociente de potencias en ambos miembros de la igualdad.
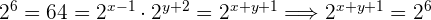
Así, se obtiene el sistema de  igualando los exponentes de cada ecuación pues tienen la misma base.
igualando los exponentes de cada ecuación pues tienen la misma base.
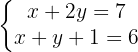
2 Aplicación del método de sustitución para resolver el sistema de 
El método de sustitución consiste de despejar una de las incógnitas de una ecuación para después sustituir la expresión obtenida en la otra ecuación, hallando así el valor de la segunda incógnita:
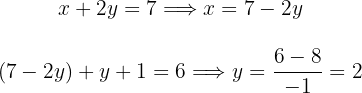
Sustituyendo el valor de  en la ecuación
en la ecuación 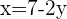 se tiene que
se tiene que  . Por tanto, la solución del sistema es
. Por tanto, la solución del sistema es 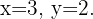
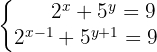
1 Reconocimiento de los exponentes y sus bases
En la segunda ecuación se aplica el producto de potencias para expresar las sumas y restas que aparecen en los exponentes como multiplicaciones y divisiones:
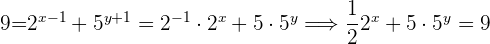
Haciendo el cambio de variable  y sustituyéndolo en la expresión obtenida anteriormente y en la primera ecuación del sistema, se obtiene el sistema
y sustituyéndolo en la expresión obtenida anteriormente y en la primera ecuación del sistema, se obtiene el sistema 
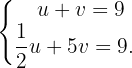
2 Aplicación del método de igualación para resolver el sistema de 
El método de igualación consiste en despejar la misma incógnita en ambas ecuaciones del sistema e igualar las expresiones obtenidas para hallar el valor de una de las incógnitas. En este caso de despejará la incógnita  :
:
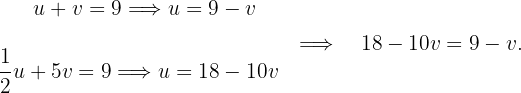
Después de calcular el valor de  se sustituye en alguna de las ecuaciones del sistema para hallar el valor de
se sustituye en alguna de las ecuaciones del sistema para hallar el valor de  . Después, se hace la sustitución de estos valores en los cambios de variable para obtener los valores
. Después, se hace la sustitución de estos valores en los cambios de variable para obtener los valores  .
.
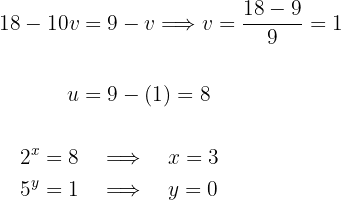
Por tanto, la solución del sistema es 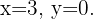
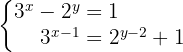
1 Reconocimiento de los exponentes y sus bases
En la segunda ecuación se aplica el producto de potencias para expresar las restas que aparecen en los exponentes como divisiones:
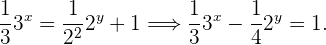
Haciendo el cambio de variable  y sustituyéndolo en la expresión obtenida anteriormente y en la primera ecuación del sistema, se obtiene el sistema
y sustituyéndolo en la expresión obtenida anteriormente y en la primera ecuación del sistema, se obtiene el sistema 
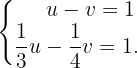
2 Aplicación del método de igualación para resolver el sistema de 
Despejando en ambas ecuaciones la incógnita  y aplicando el método de igualación, se tiene una ecuación con incógnita
y aplicando el método de igualación, se tiene una ecuación con incógnita 
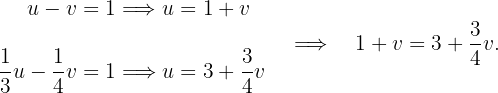
Después de calcular el valor de  se sustituye en alguna de las ecuaciones del sistema para hallar el valor de
se sustituye en alguna de las ecuaciones del sistema para hallar el valor de  . Finalmente, se hace la sustitución de estos valores en los cambios de variable para obtener los valores
. Finalmente, se hace la sustitución de estos valores en los cambios de variable para obtener los valores  .
.
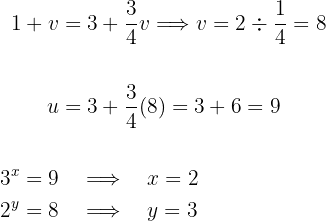
Por tanto, la solución del sistema es 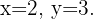
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola puede mandarme las propiedades de los logaritmos
Hola, ¿ qué propiedad podemos utilizar si por ejemplo existe un logaritmo a la 4ta potencia de ( X-1)
Hola se usa la propiedad de logx^n=n*logx, entonces log(X-1)^4=4*log(X-1).
Hola se usa la propiedad de log x^n=n*logx, entonces log(X-1)^4=4*log(X-1).
Por favor corrija la propiedad 7
Hola podrías mencionar cual es el error de la propiedad 7 o es un ejercicio?
Me imagino que se refiere a que no está al símbolo mayor. Está es el símbolo ¿, comparando X y 0.
Hola tienes razón en tu observación, pero estamos en reestructuración de nuestra plataforma y ese es un error que no se podía corregir, por ten paciencia para hacer el cambio a la nueva versión y ese error desaparecera.
Como resuelvo el cálculo log4(x)+log3(x-2)=1