Encuentra el valor de 
:
.
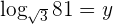Selecciona una respuesta.
1Aplicamos la definición de logaritmo
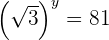
2 Escribimos como potencias
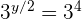
3Las bases son iguales en ambos lados de la igualdad, luego los exponentes también son iguales
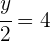
4Simplificando se obtiene
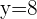
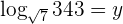
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
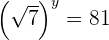
2 Escribimos como potencias
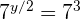
3Las bases son iguales en ambos lados de la igualdad, luego los exponentes también son iguales
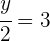
4Simplificando se obtiene
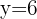
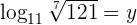
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
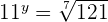
2 Escribimos como potencias
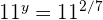
3Las bases son iguales en ambos lados de la igualdad, luego los exponentes también son iguales
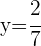
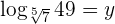
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
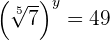
2 Escribimos como potencias
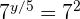
3Las bases son iguales en ambos lados de la igualdad, luego los exponentes también son iguales
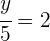
4Simplificando se obtiene
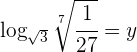
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
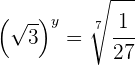
2 Escribimos como potencias
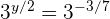
3Las bases son iguales en ambos lados de la igualdad, luego los exponentes también son iguales
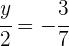
4Simplificando se obtiene
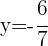
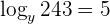
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
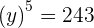
2 Escribimos como potencias
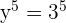
3Los exponentes son iguales en ambos lados de la igualdad, luego las bases también son iguales
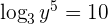
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
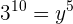
2 Escribimos como potencias
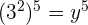
3Los exponentes son iguales en ambos lados de la igualdad, luego las bases también son iguales
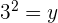
4Simplificando se obtiene
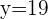
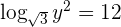
Selecciona una respuesta.
1Aplicamos la definición de logaritmo
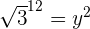
2 Escribimos como potencias
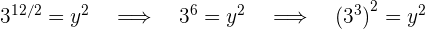
3Los exponentes son iguales en ambos lados de la igualdad, luego las también son iguales
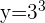
4Simplificando se obtiene
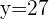
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Como resuelvo el cálculo log4(x)+log3(x-2)=1
Necesito resolver estos ejercicios.aplica las propiedades logarítmicas las siguientes expresiones.a)log4(2/6) b)log4(4.5)
310=902,5/8,69ª
Quiero despejar a de allí
Es unpoco largo, es confuso vuando pone laprimera definicion logaX=Y, y dice que X es la ingonita. log aY=X lo expresa mejor
Hola agradecemos tu comentario pues nos ayuda a ser mas claros al explicar, vamos a analizar tu sugerencia para hacer los cambios necesarios.
-6(-×+3)/2