Definición de logaritmo
Exponente al que hay que elevar un número, llamado base, para obtener otro número determinado. Un logaritmo busca el exponente 
de una base 
que se ha empleado para llegar a un determinado resultado 
.
Ejemplo:
Si tengo de base 
y como resultado 
, ¿a qué exponente se debe elevar el 
para que nos dé como resultado 
? Como te darás cuenta el valor del exponente que se utilizó para llegar al resultado con la base es 
.
La notación correspondiente para representar a un logaritmo es la siguiente:
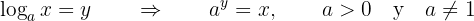
donde es la base, el resultado y el exponente buscado. Hay que recalcar que se deben cumplir las condiciones de que la base sea positiva 
y distinta a uno .
De la definición de logaritmo podemos decir que:
- No existe el logaritmo con base negativa.
- No existe el logaritmo de un número negativo.
- No existe el logaritmo de cero.
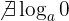
- El logaritmo de 1 es cero.
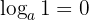
- El logaritmo en base
a de a es igual a 
.
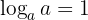
- El logaritmo en base a de una potencia en base a es igual al exponente.
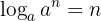
Propiedades de los logaritmos
1 El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
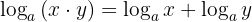
Ejemplo:
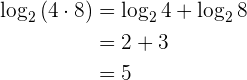
2 El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:
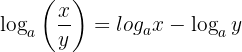
Ejemplo:
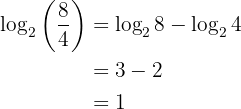
3 El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:
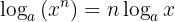
Ejemplo:
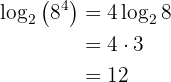
4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
Ejemplo:
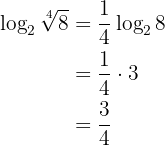
5 Cambio de base:
Ejemplo:
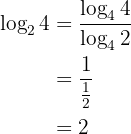
Los logaritmos se han convertido desde su creación en una herramienta importante para el cálculo de operaciones con números muy grandes, debido a que tienen la propiedad de trabajar con exponentes y convierte los problemas de multiplicación en problemas de suma. El logaritmo también, gracias a sus propiedades, permite simplificar diversas operaciones matemáticas. Por esto y más vale la pena su estudio.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Como resuelvo el cálculo log4(x)+log3(x-2)=1
Necesito resolver estos ejercicios.aplica las propiedades logarítmicas las siguientes expresiones.a)log4(2/6) b)log4(4.5)
310=902,5/8,69ª
Quiero despejar a de allí
Es unpoco largo, es confuso vuando pone laprimera definicion logaX=Y, y dice que X es la ingonita. log aY=X lo expresa mejor
Hola agradecemos tu comentario pues nos ayuda a ser mas claros al explicar, vamos a analizar tu sugerencia para hacer los cambios necesarios.
-6(-×+3)/2