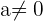un número fijo, entonces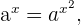
es una ecuación exponencial.
Existen varias propiedades de los exponentes que nos servirán para resolver dichas ecuaciones,
1
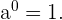
2
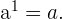
3
Si 
es un número natural,
4
Si 
son números naturales,
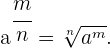
5
Si son números naturales,
6
Si son números naturales,
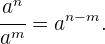
7
Si son números naturales,
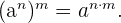
8
Si es un número natural,
9
Si es un número natural,
10
Si es un número natural,
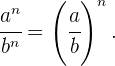
Las anteriores propiedades un conjunto con la siguiente relación forman la receta necesaria para resolver ecuaciones exponenciales. Sean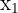 
y 
dos variables, entonces
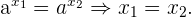
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola puede mandarme las propiedades de los logaritmos
Hola, ¿ qué propiedad podemos utilizar si por ejemplo existe un logaritmo a la 4ta potencia de ( X-1)
Hola se usa la propiedad de logx^n=n*logx, entonces log(X-1)^4=4*log(X-1).
Hola se usa la propiedad de log x^n=n*logx, entonces log(X-1)^4=4*log(X-1).
Por favor corrija la propiedad 7
Hola podrías mencionar cual es el error de la propiedad 7 o es un ejercicio?
Me imagino que se refiere a que no está al símbolo mayor. Está es el símbolo ¿, comparando X y 0.
Hola tienes razón en tu observación, pero estamos en reestructuración de nuestra plataforma y ese es un error que no se podía corregir, por ten paciencia para hacer el cambio a la nueva versión y ese error desaparecera.
Como resuelvo el cálculo log4(x)+log3(x-2)=1