Capítulos
La velocidad en una dimensión es un concepto fundamental en la física que describe la rapidez y dirección de un objeto en línea recta. Se refiere al cambio de posición de un objeto con respecto al tiempo y es esencial para comprender el movimiento de objetos en una dimensión espacial. En este contexto, exploraremos los principios y las fórmulas clave relacionadas con la velocidad unidimensional y cómo se aplica a situaciones del mundo real.

Rapidez y velocidad
La rapidez de un objeto se define como el cociente de la distancia recorrida y el intervalo de tiempo empleado para recorrerla.
La unidad de rapidez admite cualquier combinación de unidades de distancia y tiempo. Para vehículos suele emplearse las unidades de kilómetros por hora (km/h) o millas por hora (mi/h) como puedes verificar en el velocímetro de un automóvil. Cuando las distancias recorridas son pequeñas, suele emplearse las unidades de metros por segundo (m/s) o pies por segundo (ft/s).
La velocidad es una cantidad vectorial que combina las ideas de rapidez y dirección de movimiento.
Las unidades empleadas en la velocidad, al igual que en la rapidez, admite cualquier combinación de unidades de distancia y tiempo con la adición de la dirección, la cual frecuentemente se expresa mediante grados y puntos cardinales.
Ejemplo: Un ciclista se mueve en línea recta a 10 km/h es un ejemplo de rapidez; mientras que si añadimos una dirección estariamos expresando una velocidad, como lo es: un ciclista se mueve en línea recta a 10 km/h en dirección este.
Rapidez promedio
La rapidez promedio es la distancia total recorrida entre el tiempo total empleado
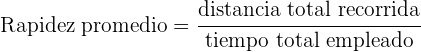
Si consideramos la posición inicial se representa por 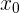 , la posición final por
, la posición final por 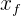 , el tiempo inicial por
, el tiempo inicial por 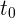 y el tiempo final por
y el tiempo final por 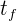 , entonces la distancia total recorrida se representa por
, entonces la distancia total recorrida se representa por 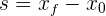 y el tiempo total empleado por
y el tiempo total empleado por 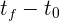 .
.
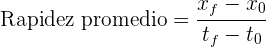
Debe tenerse cuidado con la distancia total recorrida, ya que si la partícula recorre una distancia y luego regresa a su posición inicial, entonces 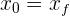 . En estos casos tenemos que encontrar la posición en la que llega e inicia su retorno, llamemosle
. En estos casos tenemos que encontrar la posición en la que llega e inicia su retorno, llamemosle 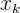 , entonces se tiene
, entonces se tiene 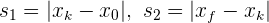 y la distancia total recorrida está dada por
y la distancia total recorrida está dada por
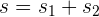
Ejemplo: Una persona corre en línea recta una distancia de 5 km y para ello emplea media hora. ¿Cuál es su rapidez promedio?
1 Representamos graficamente el problema para tener una mejor comprensión del mismo.
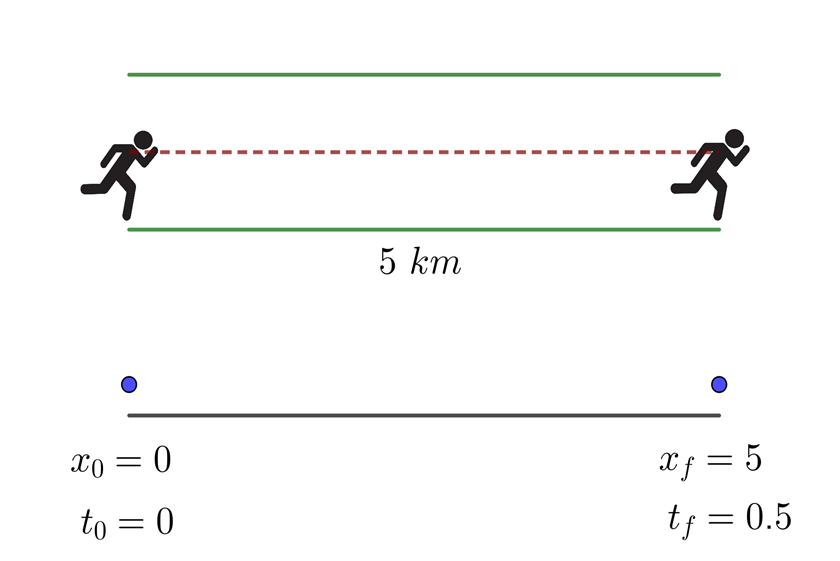
2Identificamos los datos conocidos y verificamos si el corredor avanzó siempre o tuvo algún retorno. En este ejemplo no se tienen retornos por lo que
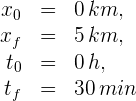
3Verificamos que se tengan las mismas unidades. Notamos que el tiempo final está dado en minutos, entonces lo convertimos a horas
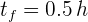
4Sustituimos en la ecuación de rapidez promedio
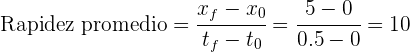
Así, la rapidez promedio es de 10 km/h.
Ejemplo: Una persona corre en línea recta una distancia de 5 km, da vuelta y retorna al punto inicial, para lo cual emplea media 50 minutos. ¿Cuál es la rapidez promedio de la persona?
1 Representamos graficamente el problema para tener una mejor comprensión del mismo.
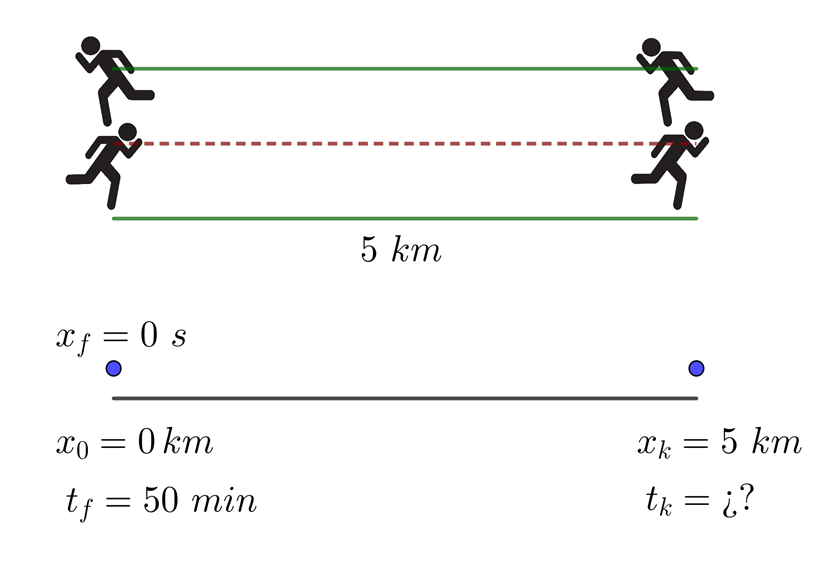
2Identificamos los datos conocidos y verificamos si el corredor avanzó siempre o tuvo algún retorno. En este ejemplo se tiene un retorno a la posición de inicio
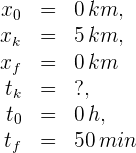
Notamos que no es necesario conocer el tiempo en que el corredor retorna, ya que el tiempo total del recorrido se obtiene empleando los tiempos final e inicial. Ahora calculamos las distancias de ida y retorno
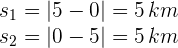
3Verificamos que se tengan las mismas unidades. Notamos que el tiempo final está dado en minutos, entonces lo convertimos a horas
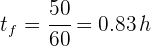
4Sustituimos en la ecuación de rapidez promedio
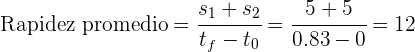
Así, la rapidez promedio es de 12 km/h.
Rapidez instantánea
Durante el movimiento de un objeto o partícula, esta puede iniciar del reposo y aumentar su rapidez o disminuirla para deternerse. La rapidez promedio indica la rapidez constante que se tendría en cualquier momento del movimiento; esta rapidez podría no coincidir con la que presenta la partícula en el transcurso de su trayectoria.
La rapidez instantánea en 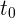 se obtiene tomando el límite en la fórmula de rapidez promedio
se obtiene tomando el límite en la fórmula de rapidez promedio
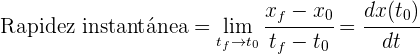
Podemos generalizar que la rapidez instantánea en cualquier tiempo  es igual al valor absoluto de la derivada de la función posición evaluada en el tiempo
es igual al valor absoluto de la derivada de la función posición evaluada en el tiempo  . El valor absoluto se requiere para garantizar que la distancia recorrida dada por la función de posición, sea positiva
. El valor absoluto se requiere para garantizar que la distancia recorrida dada por la función de posición, sea positiva
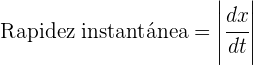
Ejemplo: Una partícula se mueve horizontalmente y su posición varía con el tiempo de acuerdo a la función 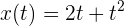 , donde
, donde  y
y  están dados en metros y segundos, respectivamente. Encuentra la rapidez instantánea de la partícula a los 2 segundos.
están dados en metros y segundos, respectivamente. Encuentra la rapidez instantánea de la partícula a los 2 segundos.
1Sabemos que la rapidez instantánea se obtiene del valor absoluto de la derivada de la función posición. Derivamos la función posición y tenemos
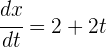
2Sustituimos el tiempo 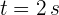
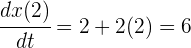
3Así, la rapidez instantánea en 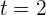 es
es
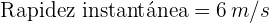
Velocidad promedio
La velocidad promedio es el desplazamiento de la partícula entre el tiempo total empleado para dicho desplazamiento
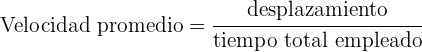
Si consideramos la posición inicial se representa por 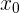 , la posición final por
, la posición final por 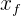 , el tiempo inicial por
, el tiempo inicial por 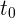 y el tiempo final por
y el tiempo final por 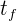 , entonces el desplazamiento se representa por
, entonces el desplazamiento se representa por 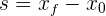 y el tiempo total empleado por
y el tiempo total empleado por 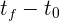
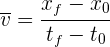
Observamos que el desplazamiento es distinto de la distancia total recorrida, ya que si la partícula recorre una distancia y luego regresa a su posición inicial, entonces el desplazamiento es cero, mientras que la distancia total recorrida es positiva. De hecho, el desplazamiento es un vector con extremo inicial 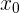 y extremo final
y extremo final 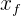 , mientras que la distancia total recorrida es un escalar.
, mientras que la distancia total recorrida es un escalar.
Ejemplo: Una persona corre en línea recta una distancia de 5 km, da vuelta y retorna al punto inicial, para lo cual emplea media 50 minutos. ¿Cuál es la velocidad promedio de la persona?
1 La representación gráfica de el problema es la misma de el ejemplo de rapidez promedio.
2Identificamos los datos conocidos. Al tratarse de velocidad solamente nos interesa las posiciones inicial y final
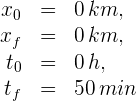
3Verificamos que se tengan las mismas unidades. Notamos que el tiempo final está dado en minutos, entonces lo convertimos a horas
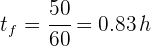
4Sustituimos en la ecuación de velocidad promedio
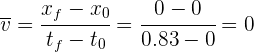
Así, la rapidez promedio es de 0 km/h.
En este ejemplo observamos que la velocidad promedio no es igual a la rapidez promedio. A partir de las posiciones inicial y final podemos encontrar la dirección de la velocidad promedio:
Si 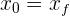 , entonces
, entonces 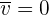 .
.
Si 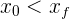 , entonces
, entonces 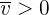 y se encuentra en la dirección que se eligio como positiva.
y se encuentra en la dirección que se eligio como positiva.
Si 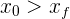 , entonces
, entonces 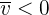 y se encuentra en la dirección que se eligio como negativa.
y se encuentra en la dirección que se eligio como negativa.
Velocidad instantánea
La velocidad instantánea en 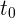 se obtiene tomando el límite en la fórmula de velocidad promedio
se obtiene tomando el límite en la fórmula de velocidad promedio
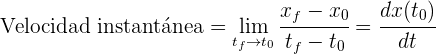
Podemos generalizar que la velocidad instantánea en cualquier tiempo  es igual a la derivada de la función posición evaluada en el tiempo
es igual a la derivada de la función posición evaluada en el tiempo 
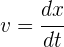
Notamos que la rapidez instantánea es igual a la magnitud positiva de la velocidad instantánea, por ello son indistinguibles salvo el signo.
Ejemplo: Una partícula se mueve horizontalmente y su posición varía con el tiempo de acuerdo a la función 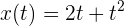 , donde
, donde  y
y  están dados en metros y segundos, respectivamente. Encuentra la velocidad instantánea de la partícula a los 2 segundos.
están dados en metros y segundos, respectivamente. Encuentra la velocidad instantánea de la partícula a los 2 segundos.
1Sabemos que la velocidad instantánea se obtiene de la derivada de la función posición. Derivamos la función posición y tenemos
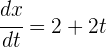
2Sustituimos el tiempo 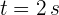
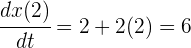
3Así, la velocidad instantánea en 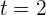 es
es
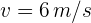
Velocidad constante
Si la velocidad de una partícula es constante, entonces su velocidad instantánea es igual a la velocidad promedio durante el intervalo de tiempo, así se obtiene la ecuación
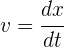
En general, el tiempo inicial es 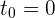 y el tiempo final es
y el tiempo final es 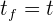 , por lo que escribiendo la diferencial de la función de posición e integrando se tiene
, por lo que escribiendo la diferencial de la función de posición e integrando se tiene
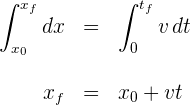
Ejemplo: Una persona se mueve a lo largo de una línea recta con rapidez constante y después de 6 segundos recorre 10 metros. Encuentra la velocidad de la persona.
1Identificamos los datos conocidos
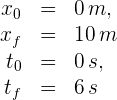
2Sabemos que la velocidad es constante ya que tiene rapidez constante, por lo que empleamos la fórmula de velocidad constante
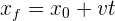
3Sustituimos y obtenemos
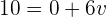
4Así, la velocidad constante es
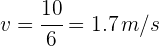
Resumir con IA:













Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker