El tiro parabólico es un fenómeno físico que describe el movimiento de un objeto lanzado en un ángulo respecto a la horizontal. Este tipo de movimiento sigue una trayectoria curva conocida como parábola, y su estudio es esencial en campos como la física y la ingeniería. Los ejercicios de tiro parabólico son una herramienta fundamental para comprender y aplicar los principios de la cinemática y la dinámica en situaciones prácticas.
En estos ejercicios, se exploran conceptos como la altura máxima alcanzada por el proyectil, el alcance horizontal, la velocidad inicial y el ángulo de lanzamiento.
Una pelota se lanza a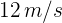 
y a un ángulo de 
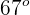respecto a la horizontal. ¿Cuál es su altura a los 2 segundos?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es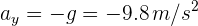 
. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
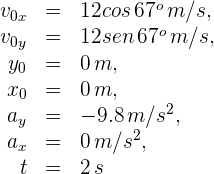
3 Para calcular la altura usamos la fórmula
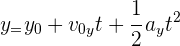
4Sustituimos los datos conocidos
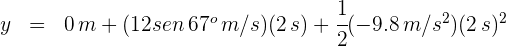
de donde se obtiene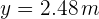 
.
Un avión con velocidad de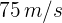 
deja caer una caja de provisiones a 500 metros del suelo. ¿Cuál es el desplazamiento de la caja a los 2 segundos?
1Establecemos las direcciones hacia abajo y a la derecha como positivas; con ello, la aceleración vertical es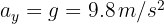 
. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
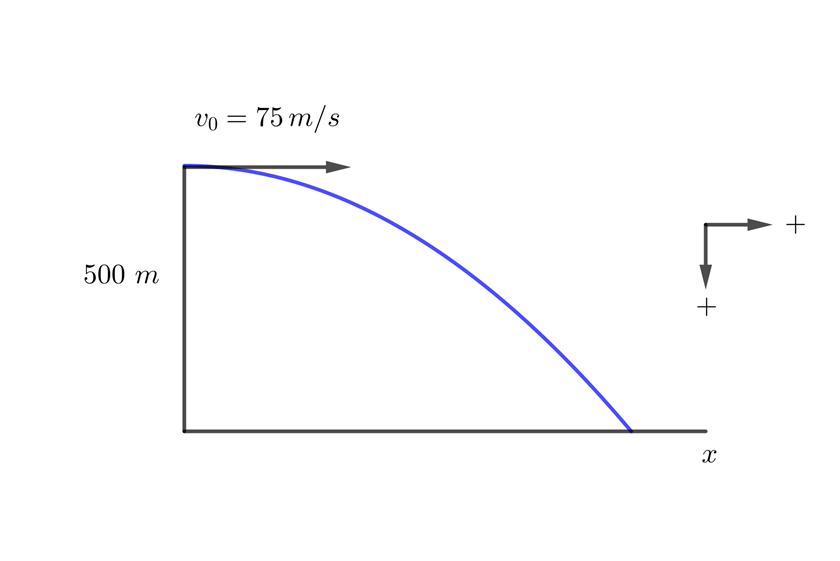
2 Indicamos los datos conocidos
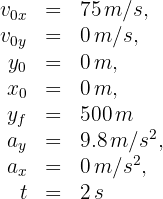
3 Para calcular la distancia que recorre la caja en 2 segundos, usamos la fórmula
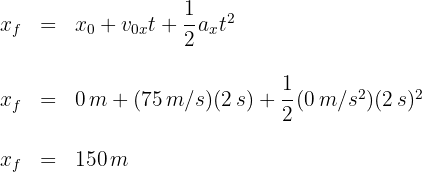
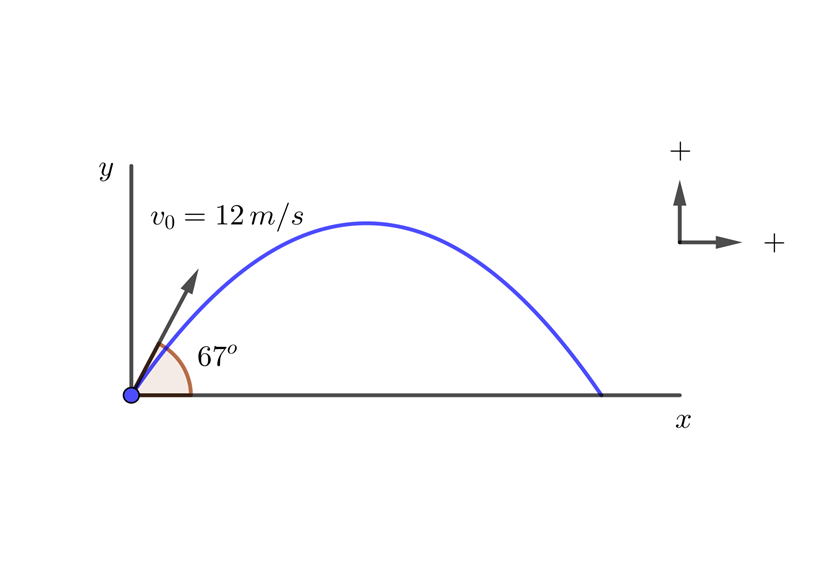
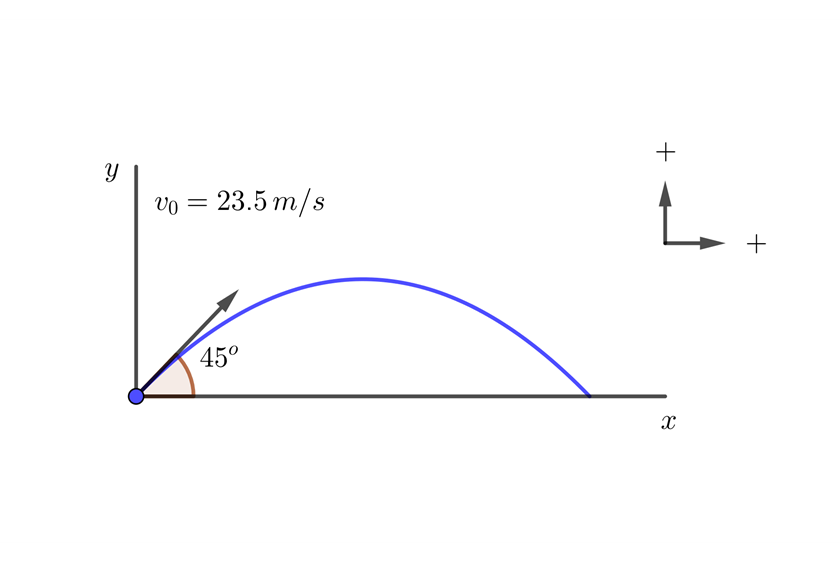
Se dispara un proyectil desde el nivel del suelo con un ángulo de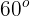 
con respecto al suelo. La velocidad inicial del proyectil es 
, ¿cuál es la altura máxima que alcanza el proyectil y en cuánto tiempo la alcanza?
1 La altura máxima del proyectil se encuentra con la parte vertical del movimiento
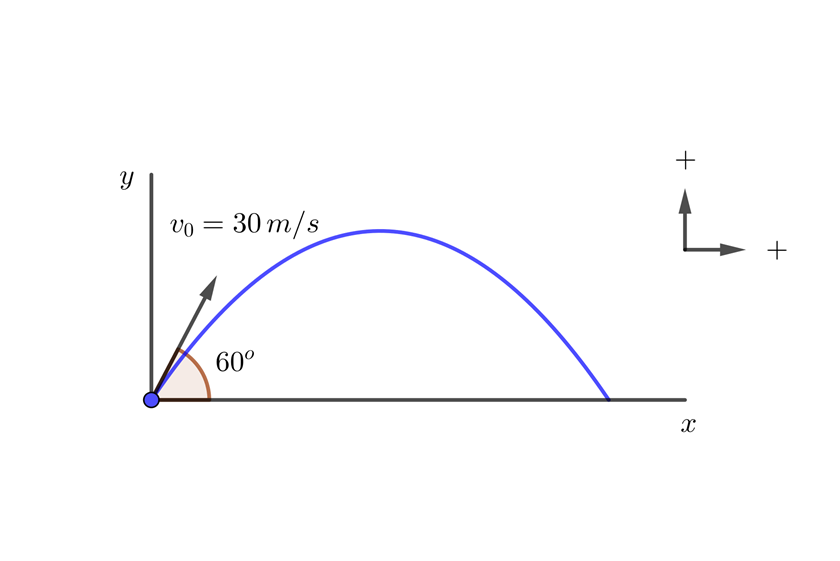
Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 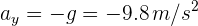. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
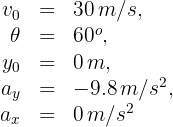
3 Calculamos las componentes horizontal y vertical de la velocidad inicial
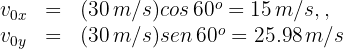
4Notamos que al alcanzar su altura máxima
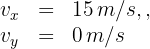
5Como en la parte vertical del movimiento la aceleración es constante, se tiene un problema de MRUA, por ello empleamos la fórmula
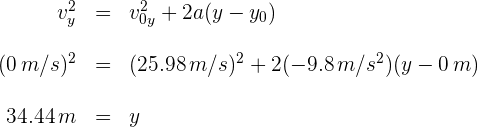
6Para encontrar el tiempo, empleamos
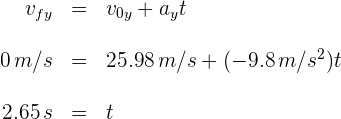
Un jugador de la NFL realiza un despeje con velocidad inicial de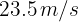 
con un ángulo de 
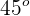respecto al suelo. ¿Cuál es el tiempo de vuelo del balón?, ¿cuál es el alcance horizontal del balón?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 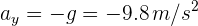. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
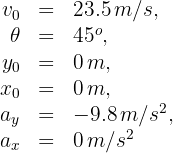
3 Calculamos las componentes horizontal y vertical de la velocidad inicial
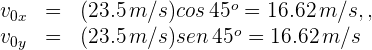
4Notamos que para encontrar el tiempo de vuelo
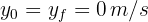
5Como en la parte vertical del movimiento la aceleración es constante, se tiene un problema de MRUA, por ello sustituimos los datos conocidos en la fórmula
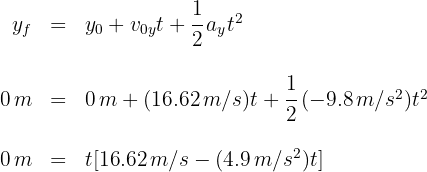
de donde se obtiene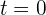 
y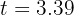 
segundos, que corresponden a las posiciones inicial y final del balón, respectivamente.
6Para encontrar el alcance horizontal, empleamos
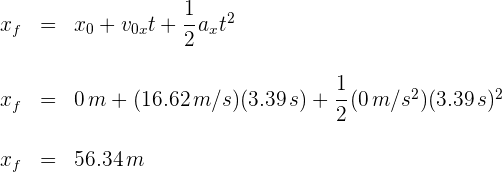
En la NFL la distancia se mide en yardas, por lo que el alcance horizontal es igual a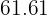 
yardas.
Un jugador de futbol se encuentra a 70 metros de la portería contraria y en pocesión del balón, observa que el guardameta se encuentra fuera del área y estima que le tomará al menos 5 segundos el regresar al arco. Si el jugador golpea el balón a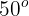 
con respecto al suelo. Encuentra velocidad a la que debe golpear el balón para que este entre en la portería.
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 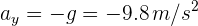. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
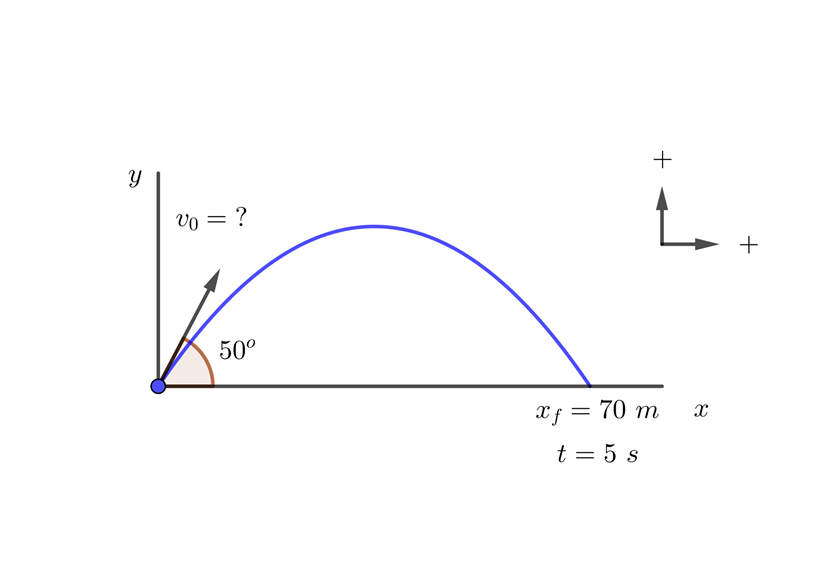
2 Indicamos los datos conocidos
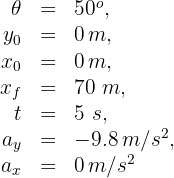
3 Expresamos en términos de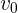 
las componentes horizontal y vertical de la velocidad inicial
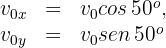
4Como en la parte horizontal del movimiento la aceleración es cero, la velocidad es constante y se tiene un problema de MRU, por ello sustituimos los datos conocidos en la fórmula
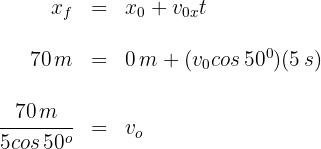
de donde se obtiene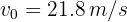 
.
Un jugador de beisbol lanza la pelota con un ángulo de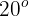 
respecto de la horizontal a 
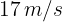. Si un compañero recibe la pelota a la misma altura que fue lanzada, ¿a qué distancia se encuentran separados ambos jugadores?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 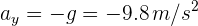. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
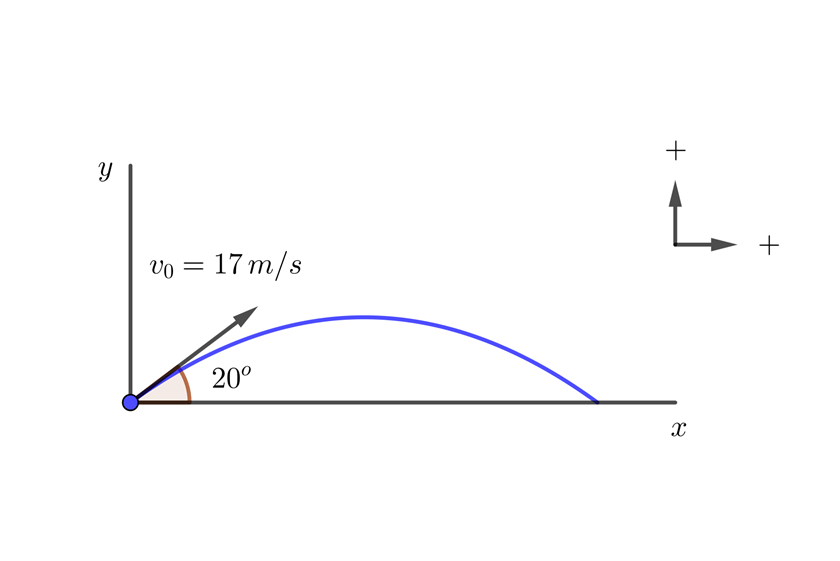
2 Indicamos los datos conocidos
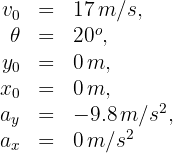
3 Calculamos las componentes horizontal y vertical de la velocidad inicial
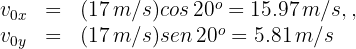
4La distancia entre los dos beisbolistas es igual al alcance horizontal. Para encontrar este alcance se requiere el tiempo de vuelo
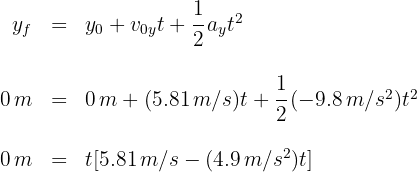
de donde se obtiene 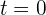y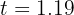 
segundos, que corresponden a las posiciones inicial y final de la pelota, respectivamente.
5Para encontrar el alcance horizontal, empleamos
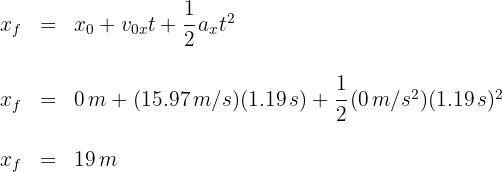
Se patea un balón desde el suelo a un ángulo de 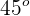y con velocidad inicial de 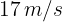. ¿Cuál es el alcance horizontal del balón?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 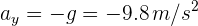. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
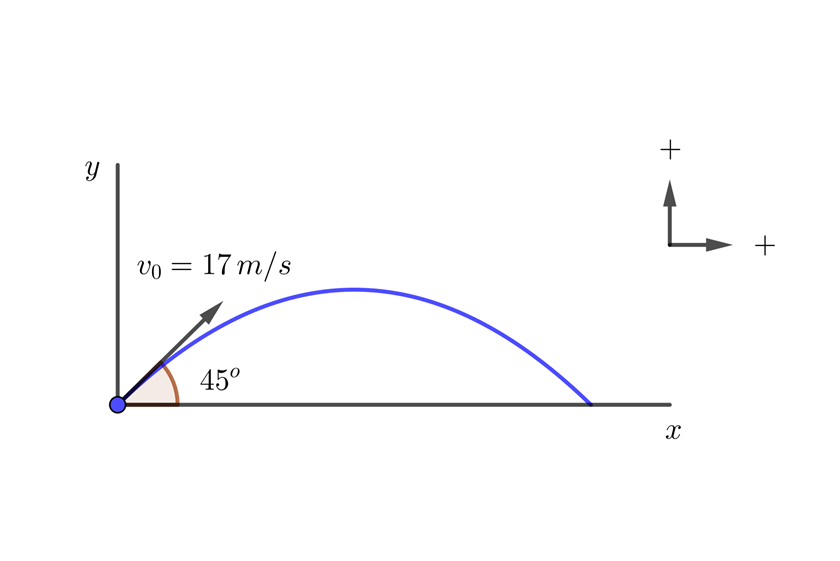
2 Indicamos los datos conocidos
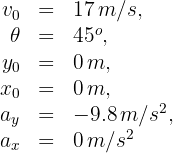
3 Calculamos las componentes horizontal y vertical de la velocidad inicial
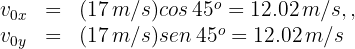
4Para encontrar este alcance se requiere el tiempo de vuelo
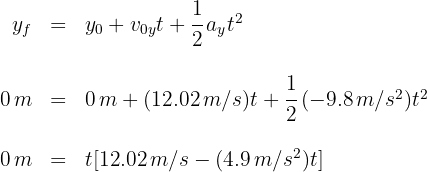
de donde se obtiene 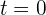y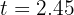 
segundos, que corresponden a las posiciones inicial y final del balón, respectivamente.
5Para encontrar el alcance horizontal, empleamos
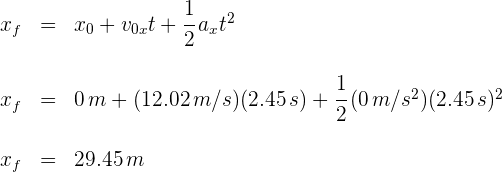
Se disparan dos proyectiles desde el suelo, ambas con velocidad inicial de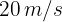 
y ángulos de 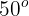y 
. ¿Cómo son los alcances de ambos proyectiles?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 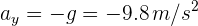. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
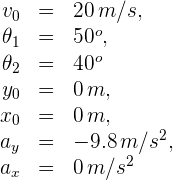
3 Calculamos las componentes horizontal y vertical de la velocidad inicial del primer proyectil
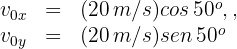
Para el segundo proyectil
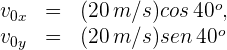
4Para encontrar el alcance se requiere el tiempo de vuelo. Para el primer proyectil se tiene
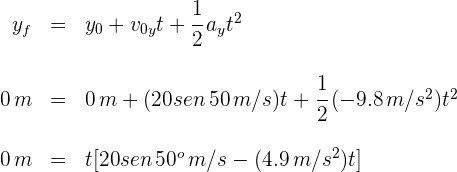
de donde se obtiene 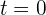y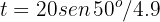 
segundos, que corresponden a las posiciones inicial y final del balón, respectivamente.
Para el segundo proyectil se tiene
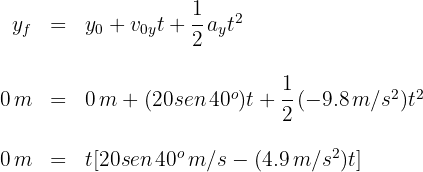
de donde se obtiene 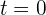y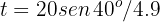 
segundos, que corresponden a las posiciones inicial y final del balón, respectivamente.
5El alcance horizontal del primer proyectil
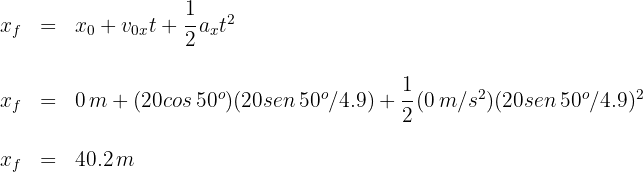
El alcance horizontal del segundo proyectil
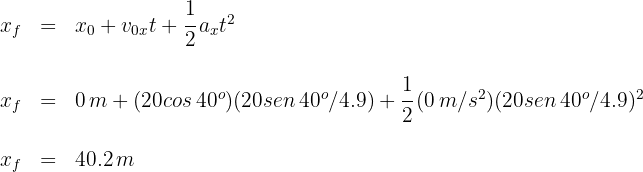
Luego, ambos alcances horizontales son iguales. De hecho, los alcances de cualesquiera dos ángulos complementarios son iguales.
Una bala se dispara horizontalmente a 2 metros sobre el nivel del suelo. Si la velocidad inicial de la bala es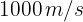 
. ¿En cuánto tiempo choca la bala con el suelo?
1Establecemos las direcciones hacia abajo y a la derecha como positivas; con ello, la aceleración vertical es 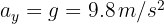. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
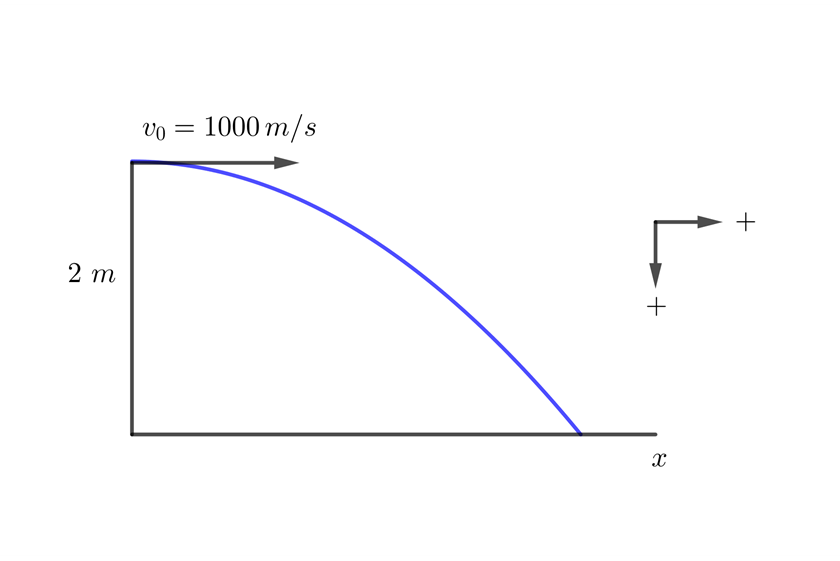
2 Indicamos los datos conocidos
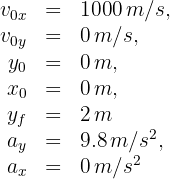
3 Para calcular el tiempo de vuelo, usamos la fórmula
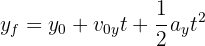
4Sustituimos los datos conocidos
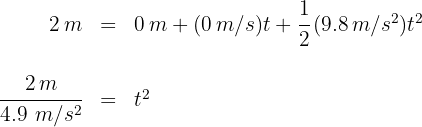
de donde se obtiene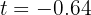 
y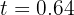 
segundos. Elegimos el tiempo positivo, ya que no tiene sentido el tiempo negativo.
Un avión con velocidad de 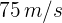deja caer una caja de provisiones a 500 metros del suelo. ¿Cuál es el desplazamiento de la caja?
1Establecemos las direcciones hacia abajo y a la derecha como positivas; con ello, la aceleración vertical es 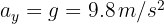. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
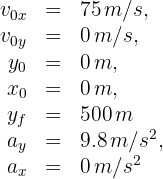
3 Para calcular el tiempo de vuelo, usamos la fórmula
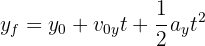
4Sustituimos los datos conocidos
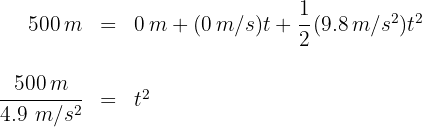
de donde se obtiene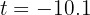 
y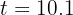 
segundos. Elegimos el tiempo positivo, ya que no tiene sentido el tiempo negativo.
5 Para calcular la distancia que recorre la caja, usamos la fórmula
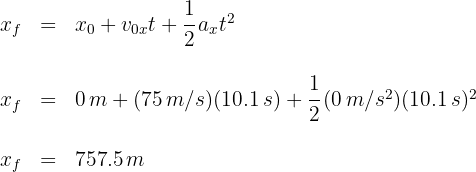
Si tienes dudas, aquí puedes consultar la teoría.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker