La cinemática tiene diversas aplicaciones prácticas y cotidianas, desde estimar la velocidad inicial horizontal del balón en un disparo a gol en fútbol hasta diversas situaciones, como el seguimiento de vehículos, la estimación de velocidades, la predicción de trayectorias por mencionar algunas.
Un automóvil se mueve a velocidad constante de 60 kilómetros por hora durante 30 minutos, ¿cuál es la distancia recorrida por el automóvil?
1 Indicamos los datos conocidos
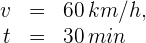
2Convertimos el tiempo a horas
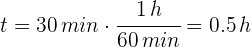
3Como la velocidad es constante, se tiene un problema de MRU, por ello empleamos la fórmula
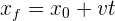
4Sustituimos los datos conocidos
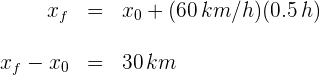
Se desea evaluar el rendimiento de un ciclísta y planificar un viaje en bicicleta. Si recorre 25 kilómetros en 1.2 horas, ¿cuál es su velocidad promedio y qué distancia recorre en los primeros 15 minutos?
1 Indicamos los datos conocidos
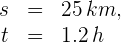
2Empleamos la fórmula de velocidad promedio
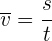
3Sustituimos los datos conocidos

4Para calcular la distancia recorrrida en los primeros 15 minutos, convertimos el tiempo a horas
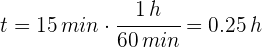
3Sustituimos los datos conocidos en la fórmula de velocidad promedio
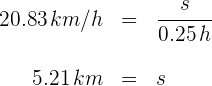
Un vehículo se mueve con una velocidad promedio de 11 metros por segundo. Si recorre 20 kilómetros, ¿cuánto tiempo le lleva realizarlo?
1 Indicamos los datos conocidos
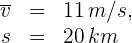
2Convertimos la velocidad a kilómetros por hora
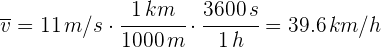
3Empleamos la fórmula de velocidad promedio
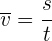
4Sustituimos los datos conocidos
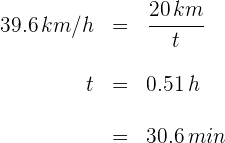
Un automóvil viaja a 50 km/h durante los primeros 20 km, luego incrementa su velocidad a 60 km/h en los siguientes 10 km, y finalmente reduce su velocidad a 40 km/h en los últimos 5 km. ¿Cuánto tiempo le tomó recorrer los 35 km?
1 Indicamos los datos conocidos

2Como la velocidad es constante por tramos, se tiene un problema de MRU, por ello empleamos la fórmula
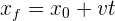
3Sustituimos los datos conocidos considerando 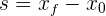
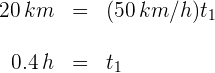
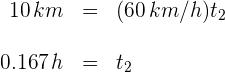
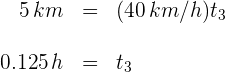
4El tiempo total empleado es
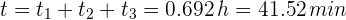
Un automóvil recorre 20 km a una velocidad promedio de 70 km/h. Un segundo automóvil recorre los primeros 15 km a una velocidad de 65 km/h. Si ambos automóviles parten del mismo punto y al mismo tiempo, ¿a qué velocidad debe ir el segundo automóvil en los últimos 5 km para llegar al mismo tiempo que el primer automóvil?
1 Calculamos el tiempo empleado por el primer automóvil para recorrer los 60 km
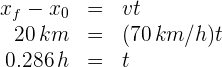
2 Calculamos el tiempo empleado por el segundo automóvil para recorrer los primeros 15 km
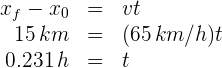
3 Notamos que el segundo automóvil recorre los últimos 5 km en 0.055 h. Calculamos la velocidad en estos 5 km
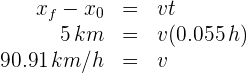
La grabación de una cámara de tráfico muestra un vehículo moviendose en una carretera recta. Si entre dos fotogramas consecutivos, el vehículo se desplaza 4 metros y el intervalo de tiempo es de 0.1 segundos, ¿cuál es la velocidad promedio del vehículo?
1 Indicamos los intervalos de distancia y tiempo conocidos
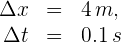
2Empleamos la fórmula de velocidad promedio
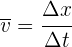
3Sustituimos los datos conocidos
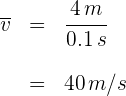
4Convertimos a kilómetros por hora
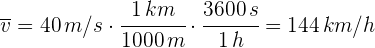
La distancia entre dos señales de tráfico es de 100 metros. Si el vehículo tarda 9 segundos es recorrerlo, ¿cuál es la velocidad promedio del vehículo?
1 Indicamos los intervalos de distancia y tiempo conocidos
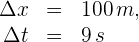
2Empleamos la fórmula de velocidad promedio
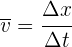
3Sustituimos los datos conocidos
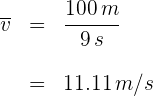
4Convertimos a kilómetros por hora
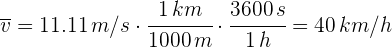
Un basquetbolista de 1.9 metros de altura lanza el balón desde la línea de tiro libre ubicada a 4.57 metros de la canasta, que se encuentra a una altura de 3.05 metros. Si el lanzamiento lo realiza con un ángulo de 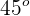 , ¿cuál es la velocidad inicial del lanzamiento para que el balón caiga en la canasta?
, ¿cuál es la velocidad inicial del lanzamiento para que el balón caiga en la canasta?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 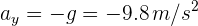 . La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
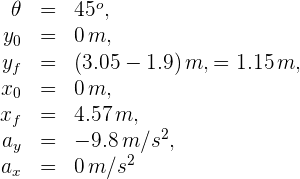
3 Representamos las componentes horizontal y vertical de la velocidad inicial
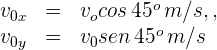
4Como en la parte vertical del movimiento la aceleración es constante, se tiene un problema de MRUA, por ello sustituimos los datos conocidos en las fórmulas de posiciones finales
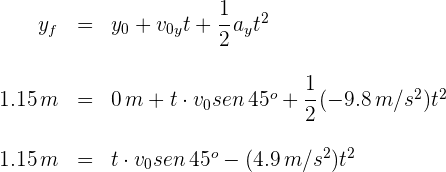
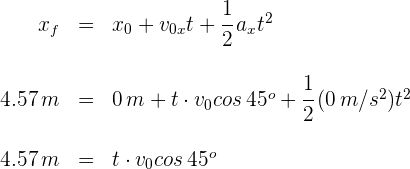
5Para encontrar la velocidad inicial, despejamos el tiempo de la segunda ecuación y lo sustituimos en la primera
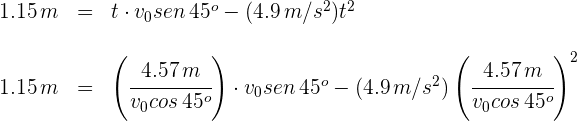
Despejando el tiempo, se obtiene
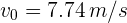
Un beisbolista conecta un cuadrangular y la pelota cae en las butacas a 8 metros por encima del punto donde fue golpeada la pelota y con una velocidad de 48 m/s a un ángulo de 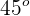 con respecto a la horizontal, ¿cuál es la velocidad inicial de la pelota cuando deja de estar en contacto con el bat?
con respecto a la horizontal, ¿cuál es la velocidad inicial de la pelota cuando deja de estar en contacto con el bat?
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 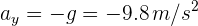 . La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
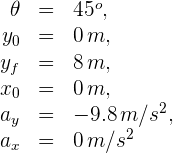
3 Representamos las componentes horizontal y vertical de la velocidad inicial
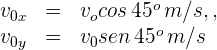
4 Como la aceleración horizontal es cero, entonces la velocidad horizontal es constante, luego
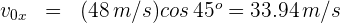
5Como en la parte vertical del movimiento la aceleración es constante, se tiene un problema de MRUA, por ello sustituimos los datos conocidos en la fórmula de velocidad final
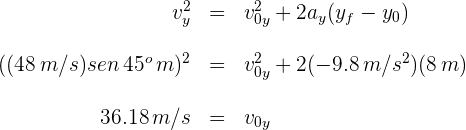
6La velocidad inicial con la que se golpea la pelota es
Un jugador de futbol se encuentra a 45 metros de la portería contraria y en pocesión del balón, observa que el guardameta se encuentra fuera del área y estima que le tomará al menos 4 segundos el regresar al arco. Si el jugador golpea el balón a 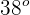 con respecto al suelo. Encuentra velocidad a la que debe golpear el balón para que este entre en la portería.
con respecto al suelo. Encuentra velocidad a la que debe golpear el balón para que este entre en la portería.
1Establecemos las direcciones hacia arriba y a la derecha como positivas; con ello, la aceleración vertical es 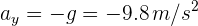 . La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
. La aceleración horizontal siempre es cero, por lo que la velocidad horizontal es constante.
2 Indicamos los datos conocidos
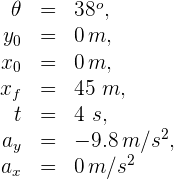
3 Expresamos en términos de 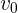 las componentes horizontal y vertical de la velocidad inicial
las componentes horizontal y vertical de la velocidad inicial
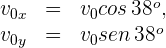
4Como en la parte horizontal del movimiento la aceleración es cero, la velocidad es constante y se tiene un problema de MRU, por ello sustituimos los datos conocidos en la fórmula
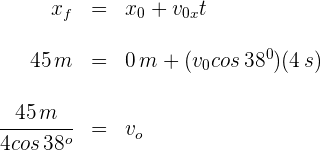
de donde se obtiene 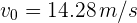 .
.
Resumir con IA:



Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker