Te presentamos una serie de ejercicios diseñados para consolidar los conocimientos adquiridos en el estudio del movimiento circular uniforme (MCU). Estos ejercicios abarcan diferentes aspectos del MCU, desde la conversión entre magnitudes lineales y angulares hasta la aplicación de fórmulas fundamentales.
Responde las siguientes preguntas:
Una partícula gira en un círculo horizontal. Si su periodo es 0.125 segundos, entonces su frecuencia es...
Selecciona una respuesta.
El periodo  es el tiempo para completar una revolución (vuelta) de la partícula en el círculo, mientras que la frecuencia es el número de revoluciones por segundo
es el tiempo para completar una revolución (vuelta) de la partícula en el círculo, mientras que la frecuencia es el número de revoluciones por segundo
Aplicamos la fórmula
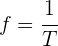
Así, el periodo es
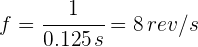
Un cuerpo gira en un círculo horizontal con una rapidez lineal de 35 m/s. Si tiene periodo 0.7 segundos, entonces el radio del círculo es...
Selecciona una respuesta.
1 Los datos conocidos son:
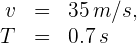
2 Para calcular el radio del círculo, empleamos la fórmula

3 Sustituimos los datos conocidos en la fórmula y obtenemos
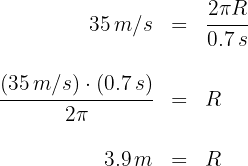
Un objeto es atado a una cuerda de un metro y se hace girar horizontalmente. Si el objeto realiza un giro en medio segundo, entonces su velocidad lineal es...
Selecciona una respuesta.
1 Los datos conocidos son:
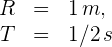
2 Para calcular la velocidad lineal, empleamos la fórmula

3 Sustituimos los datos conocidos en la fórmula y obtenemos
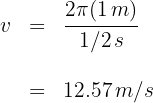
Un objeto se mueve en una pista circular de radio 3 metros y frecuencia de 5 revoluciones por segundo. La velocidad lineal es...
Selecciona una respuesta.
1 Los datos conocidos son:
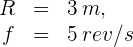
2 Para calcular la velocidad lineal, empleamos la fórmula
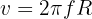
3 Sustituimos los datos conocidos en la fórmula y obtenemos
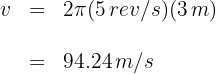
Una partícula se mueve sobre un círculo de radio 50 centímetros y realiza 3 revoluciones por segundo. Su aceleración centrípeta es...
Selecciona una respuesta.
1 Los datos conocidos son:
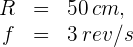
Convertimos el radio a metros
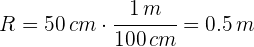
2 Para calcular la velocidad lineal, empleamos la fórmula
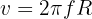
3 Sustituimos los datos conocidos en la fórmula y obtenemos
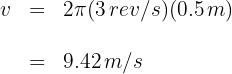
4 Para calcular la aceleración centrípeta, es decir, la aceleración que siempre se dirige hacia el centro, empleamos la fórmula
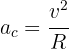
5 Sustituimos los datos conocidos en la fórmula y obtenemos
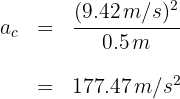
Una partícula se mueve sobre un círculo horizontal de radio 45 centímetros. Si su aceleración centrípeta es 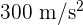 , entonces su velocidad lineal es...
, entonces su velocidad lineal es...
Selecciona una respuesta.
1 Los datos conocidos son:
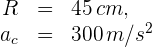
Convertimos el radio a metros
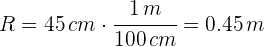
2 Para calcular la velocidad lineal, empleamos la fórmula
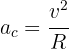
3 Sustituimos los datos conocidos en la fórmula y obtenemos
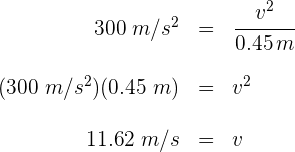
Un caballo de  cabalga en una pista circular. Si su aceleración centrípeta es
cabalga en una pista circular. Si su aceleración centrípeta es 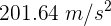 , entonces su fuerza centrípeta es...
, entonces su fuerza centrípeta es...
Selecciona una respuesta.
1 Los datos conocidos son:
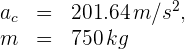
2 Para calcular la fuerza centrípeta, empleamos la fórmula
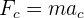
3 Sustituimos los datos conocidos en la fórmula y obtenemos
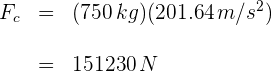
Un objeto describe una trayectoria circular horizontal y tiene aceleración de 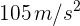 . Si su fuerza centrípeta es de
. Si su fuerza centrípeta es de 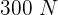 , entonces la masa del objeto es...
, entonces la masa del objeto es...
Selecciona una respuesta.
1 Los datos conocidos son:
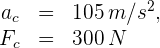
2 Para calcular la masa, empleamos la fórmula
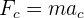
3 Sustituimos los datos conocidos en la fórmula y obtenemos
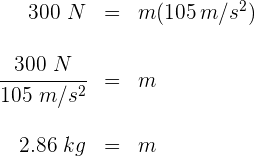
Una bicicleta gira en una pista círcular de radio 20 m, con aceleración centrípeta de 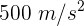 . Su velocidad angular es...
. Su velocidad angular es...
Selecciona una respuesta.
1 Los datos conocidos son:
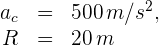
2 Para calcular la velocidad angular, empleamos la fórmula
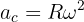
3 Sustituimos los datos conocidos en la fórmula y obtenemos
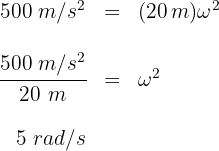
Un objeto gira en una pista círcular de radio 10 m, con velocidad angular de 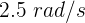 . Su aceleración centrípeta es...
. Su aceleración centrípeta es...
Selecciona una respuesta.
1 Los datos conocidos son:
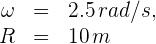
2 Para calcular la aceleración centrípeta, empleamos la fórmula
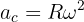
3 Sustituimos los datos conocidos en la fórmula y obtenemos
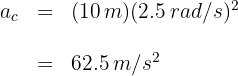
Si tienes dudas puedes consultar los ejercicios resueltos.
Resumir con IA:



Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker