Capítulos
Las fórmulas clave de cinemática son herramientas fundamentales en física, permitiendo calcular y comprender el movimiento de objetos. Estas ecuaciones, que abarcan aspectos como la posición, velocidad, aceleración y tiempo, son esenciales para resolver problemas relacionados con el movimiento. Al emplear estas fórmulas, se puede analizar y predecir el comportamiento y la trayectoria de un objeto en movimiento, brindando una base sólida para el estudio de la cinemática en distintos contextos.
Velocidad promedio e instantánea
La velocidad promedio es el desplazamiento de la partícula entre el tiempo total empleado para dicho desplazamiento
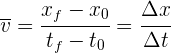
La velocidad instantánea se obtiene tomando el límite en la fórmula de velocidad promedio
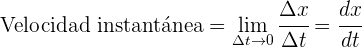
Rapidez promedio e instantánea
La rapidez promedio es la distancia total recorrida entre el tiempo total empleado
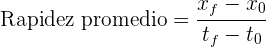
La rapidez instantánea es la magnitud de la velocidad instantánea.
Aceleración promedio e instantánea
La aceleración promedio es el cambio de velocidad de la partícula entre el tiempo total empleado
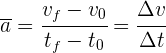
La aceleración instantánea se obtiene tomando el límite en la fórmula de velocidad promedio cuando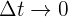 
, entonces
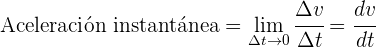
Movimiento rectilíneo uniforme
A partir de la fórmula de velocidad instantánea, con velocidad constante
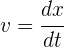
escribimos como diferenciales e integramos ambos lados de la igualdad para obtener
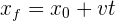
Movimiento rectilíneo uniformemente acelerado
A partir de la fórmula de aceleración instantánea, con aceleración constante
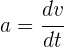
escribimos como diferenciales e integramos ambos lados de la igualdad para obtener
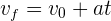
Cuando la aceleración es constante, la velocidad varía linealmente con respecto al tiempo, por lo que la velocidad promedio en cualquier intervalo de tiempo es igual al promedio de la velocidad inicial con la final
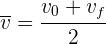
Cuando la aceleración es constante, podemos encontrar la posición final a partir del tiempo y las velocidades inicial y final aplicadas en la fórmula de la velocidad promedio
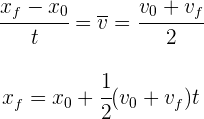
Cuando la aceleración es constante, podemos encontrar la posición final a partir de las velocidades inicial, la aceleración constante y el tiempo, sustituyendo la expresión de la velocidad final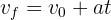 
en la fórmula anterior
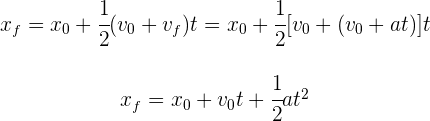
También podemos encontrar la velocidad final a partir de las velocidad inicial, la aceleración constante y la posición de la partícula sin contener el tiempo. Para esto sustituimos la expresión del tiempo de la fórmula de aceleración promedio, en la fórmula de la posición en término de sus velocidades inicial, final y el tiempo
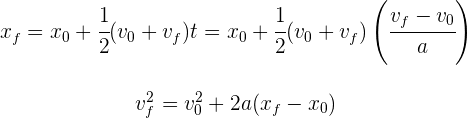
Movimiento rectilíneo con aceleración variable
A partir de las fórmulas de velocidad y aceleración instantánea, las cuales se encuentran en función del tiempo
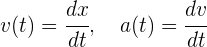
escribimos como diferenciales e integramos ambos lados de la igualdad para obtener
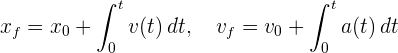
Observa que a diferencia del movimiento rectilíneo uniforme y uniformemente acelerado, donde se tiene una expresión explícita para las integrales de la velocidad y aceleración, en este caso se requiere realizar las integrales, siempre que estas sean posible de resolver.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker