Capítulos
La posición  en el tiempo
en el tiempo  de una partícula, permite una descripción completa de su movimiento. Para indicar la posición en el tiempo
de una partícula, permite una descripción completa de su movimiento. Para indicar la posición en el tiempo 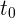 , escribimos
, escribimos 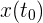 .
.
En el caso del movimiento en una dimensión, se emplea un marco de referencia particular. Comunmente se representa con una línea horizontal  (algunas veces vertical) y el tiempo solamente se expresa numericamente y no de manera gráfica
(algunas veces vertical) y el tiempo solamente se expresa numericamente y no de manera gráfica
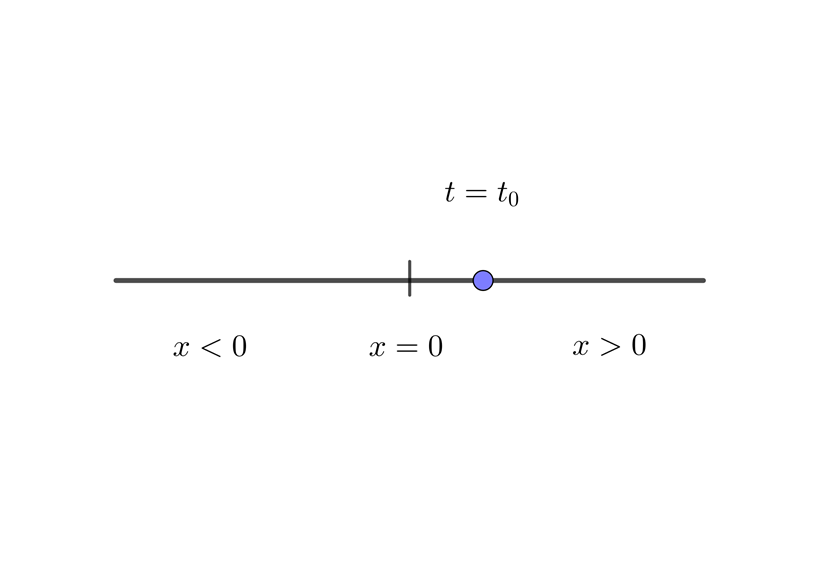
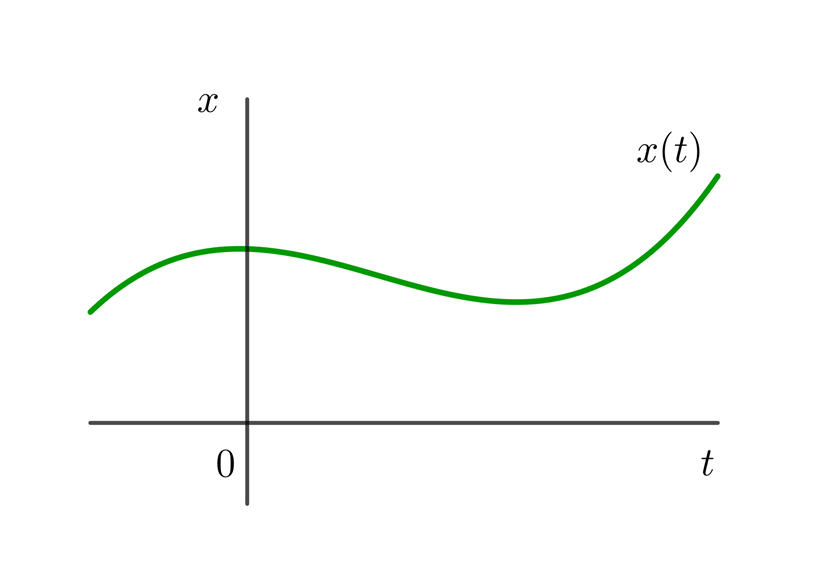
Para representar el tiempo en el movimiento unidimensional, se emplea una gráfica en dos dimensiones: el eje horizontal representando el tiempo y el eje vertical a la posición, respectivamente, por lo que la posición es una función del tiempo

Posición en ausencia de movimiento
Como no existe movimiento, la partícula permanece en la misma posición conforme transcurre el tiempo. Si la partícula se encuentra en reposo en el punto  de la coordenada
de la coordenada  , entonces su movimiento se representa con la línea horizontal
, entonces su movimiento se representa con la línea horizontal 
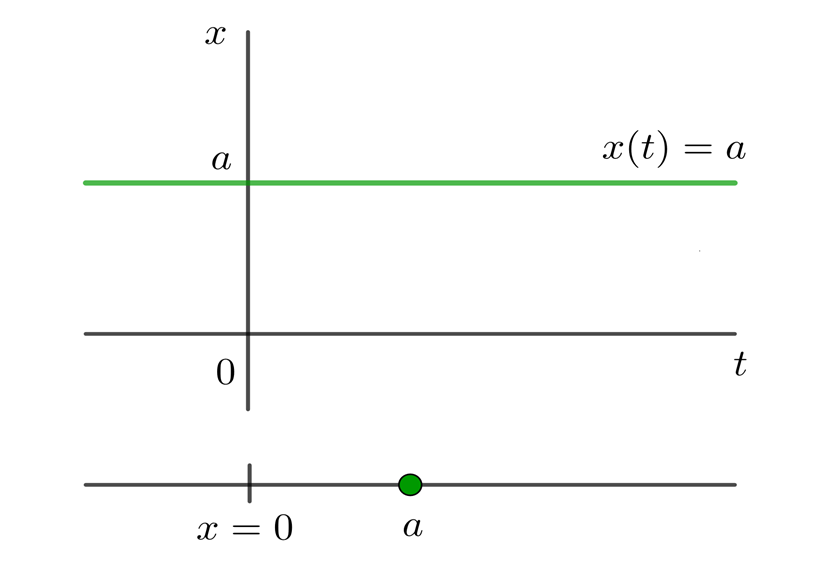
Ejemplo: La función que describe la posición de un auto que inicialmente se encuentra a 5 kilómetros del origen y cuya velocidad es 0 kilómetros por hora, viene dada por
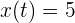
Posición en movimiento a velocidad constante
Tener velocidad constante significa que recorre la misma distancia por cada unidad de tiempo. Si la partícula se encuentra inicialmente en la posición  y se mueve a velocidad constante de
y se mueve a velocidad constante de 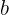 unidades de distancia por cada unidad de tiempo, podemos tabular la posición por cada unidad de tiempo y a partir de ello, deducir la función de posición
unidades de distancia por cada unidad de tiempo, podemos tabular la posición por cada unidad de tiempo y a partir de ello, deducir la función de posición
| Tiempo
| Posición
|
|---|---|
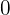 |  |
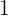 | 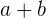 |
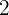 | 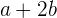 |
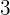 | 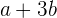 |
 |  |
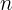 | 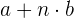 |
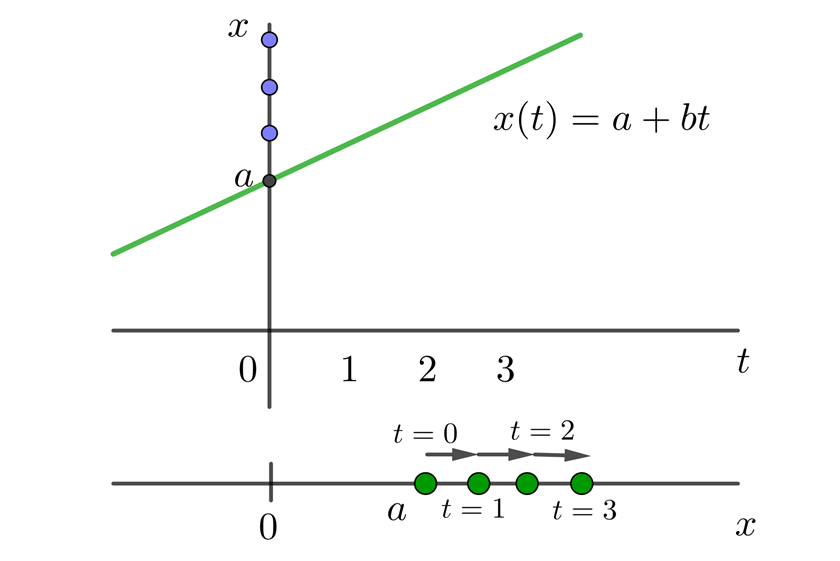
Es fácil observa que si calculamos la pendiente de cualesquiera dos puntos, esta es la misma y es igual a la velocidad de la partícula. Entonces la función de posición está dada por la línea recta
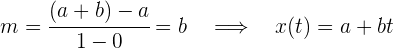
La pendiente de cualquier función, indica su cantidad de cambio, por lo que la cantidad de cambio de la posición es la velocidad y mientras mayor sea la pendiente, mayor será la velocidad
Sabemos que la derivada es una razón de cambio, por lo que la derivada de la función posición con respecto al tiempo es igual a la velocidad
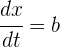
Otra forma de obtener la función de posición consiste en integrar la velocidad
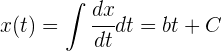
donde 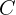 es la constante de integración. Para obtener el valor que corresponde a
es la constante de integración. Para obtener el valor que corresponde a 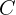 , sustituimos la condición inicial que conocemos: a tiempo 0 la partícula se encuentra en la posición
, sustituimos la condición inicial que conocemos: a tiempo 0 la partícula se encuentra en la posición 
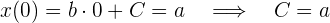
Así, la función de posición es
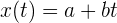
Ejemplo: Un ciclista recorre un camino recto a una velocidad constante de 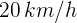 . Sí su recorrido duró 30 minutos, ¿cuál es la distancia total del recorrido?, ¿que distancia ha recorrido en 13 minutos?
. Sí su recorrido duró 30 minutos, ¿cuál es la distancia total del recorrido?, ¿que distancia ha recorrido en 13 minutos?
Primero ubicamos los datos que conocemos: la velocidad 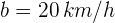 ; no se indica una posición inicial, pero ya que vamos a medir su recorrido podemos considerar
; no se indica una posición inicial, pero ya que vamos a medir su recorrido podemos considerar 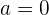 ; con el tiempo debemos ser cuidadosos ya que se requiere tener las mismas unidades, por lo que convertimos los minutos a horas, esto es,
; con el tiempo debemos ser cuidadosos ya que se requiere tener las mismas unidades, por lo que convertimos los minutos a horas, esto es, 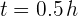 .
.
Para encontrar la distancia recorrida, buscamos su posición a los 30 minutos, para ello sustituimos los datos en la ecuación de posición
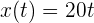
Sustituimos el tiempo equivalente a los 30 minutos
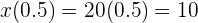
Así, la distancia total recorrida es de 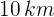
Para conocer la distancia recorrida en 13 minutos, primero convertimos esta cantidad a horas 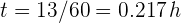 . Sustituimos este valor en la ecuación de posición
. Sustituimos este valor en la ecuación de posición
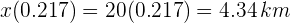
Posición en movimiento con aceleración constante
Tener aceleración constante significa que la velocidad está cambiando, ya que la aceleración es la razón de cambio de la velocidad con respecto al tiempo. Si la partícula se encuentra inicialmente en la posición  con velocidad inicial
con velocidad inicial 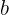 unidades de distancia por cada unidad de tiempo y aceleración constante
unidades de distancia por cada unidad de tiempo y aceleración constante 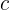 unidades de velocidad por cada unidad de tiempo, podemos tabular la velocidad por cada unidad de tiempo y ver su comportamiento
unidades de velocidad por cada unidad de tiempo, podemos tabular la velocidad por cada unidad de tiempo y ver su comportamiento
| Tiempo
| Velocidad
|
|---|---|
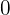 | 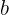 |
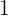 | 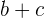 |
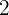 | 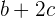 |
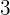 | 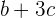 |
 |  |
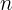 | 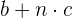 |
De la tabla se observa que la velocidad es lineal respecto al tiempo. Como la velocidad es la derivada de la posición, integrar la velocidad permite obtener la función de posición
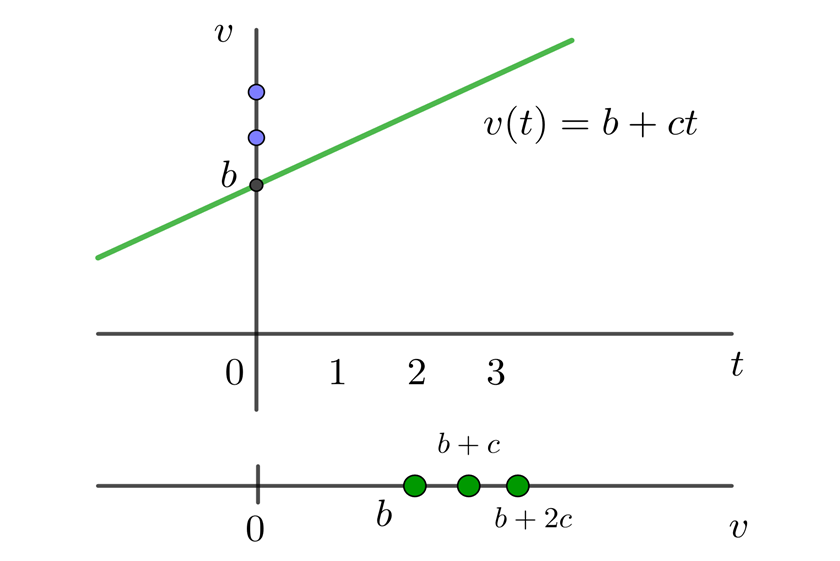
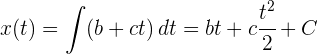
donde 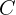 es la constante de integración. Para obtener el valor que corresponde a
es la constante de integración. Para obtener el valor que corresponde a 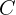 , sustituimos la condición inicial que conocemos: a tiempo 0 la partícula se encuentra en la posición
, sustituimos la condición inicial que conocemos: a tiempo 0 la partícula se encuentra en la posición 
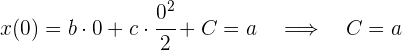
Así, la función de posición es
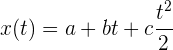
Ejemplo: El ciclista recorre un camino recto a una velocidad de 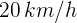 . Si al pasar por cierto punto acelera a razón de
. Si al pasar por cierto punto acelera a razón de 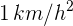 durante 12 minutos, ¿cuál es la distancia que recorrió durante los 12 minutos?
durante 12 minutos, ¿cuál es la distancia que recorrió durante los 12 minutos?
Primero ubicamos los datos que conocemos: la aceleración 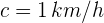 , la velocidad
, la velocidad 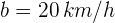 ; no se indica una posición inicial, pero ya que vamos a medir su recorrido podemos considerar
; no se indica una posición inicial, pero ya que vamos a medir su recorrido podemos considerar 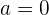 ; con el tiempo convertimos los minutos a horas, esto es,
; con el tiempo convertimos los minutos a horas, esto es, 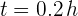 .
.
Para encontrar la distancia recorrida, buscamos su posición a los 12 minutos, para ello sustituimos los datos en la ecuación de posición
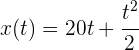
Sustituimos el tiempo equivalente a los 12 minutos
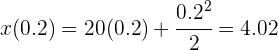
Así, la distancia total recorrida es de 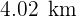
Resumir con IA:










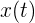
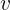



Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker