Capítulos
La cinemática en dos y tres dimensiones es una rama fascinante de la física que se enfoca en el estudio del movimiento de los objetos en el espacio tridimensional. Mientras que la cinemática en una dimensión se centra en describir el movimiento a lo largo de una línea recta, la cinemática en dos y tres dimensiones amplía este análisis para incluir movimientos en planos y en el espacio.
Este estudio nos permite modelar y prever el movimiento de partículas, objetos o sistemas en entornos más complejos, como el vuelo de un pájaro en el cielo, la trayectoria de un proyectil en el espacio, o incluso el movimiento de planetas en nuestro sistema solar.
Posición en dos dimensiones
El movimiento de una partícula u objeto en dos dimensiones da lugar a una trayectoria
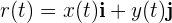
donde:
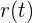es el vector posición de la partícula en un tiempo 
.
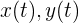son las componentes del vector 
que dan la posición de la partícula a tiempo .
Por simplicidad solamente se escribe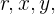 
y se indica el tiempo por separado.
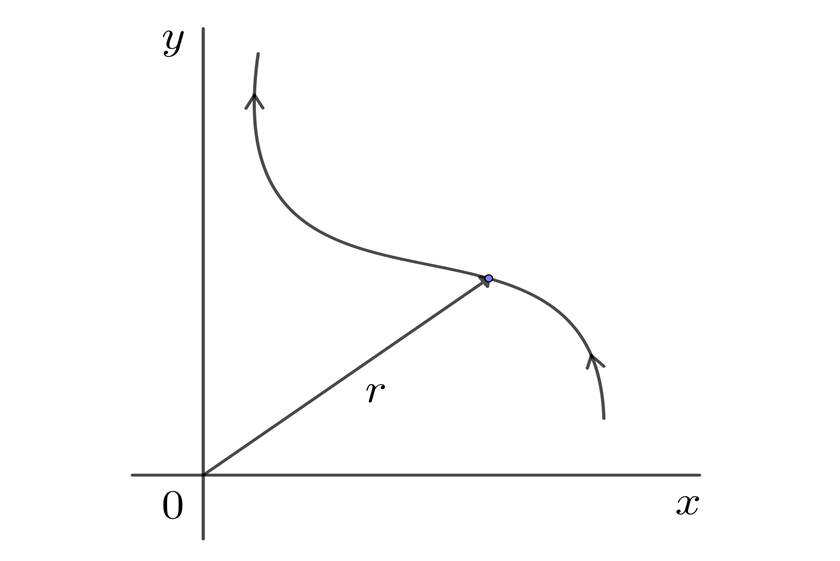
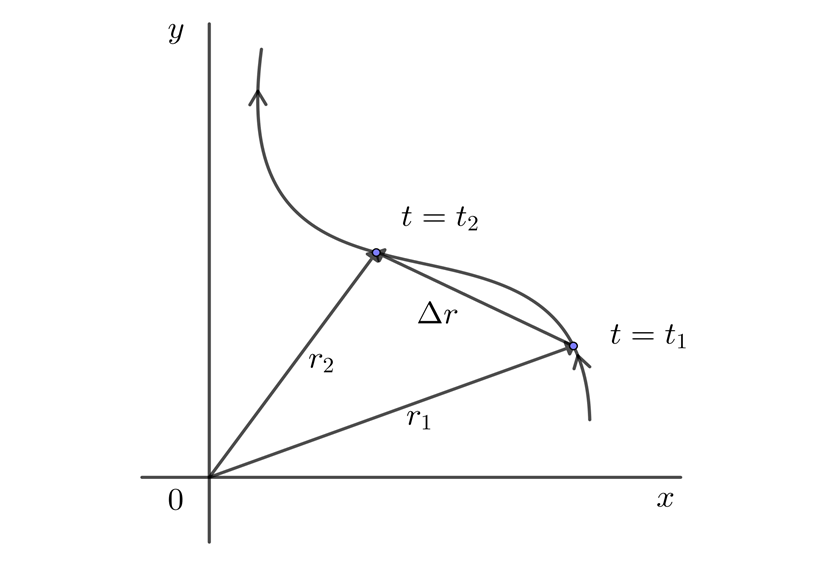
Si a tiempo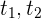 
la partícula se encuentra en la posición 
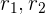respectivamente, el desplazamiento o cambio de posición en el intervalo de tiempo 
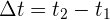, es el vector
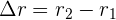
Ejemplo: Una partícula se mueve en el plano de acuerdo a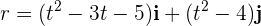 
. Si las coordenadas 
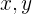están en metros y el tiempo en segundos, encuentra el desplazamiento realizado al moverse de 1 a 3 segundos.
1 Calculamos la posición a tiempo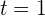 
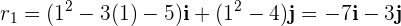
2 Calculamos la posición a tiempo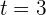 
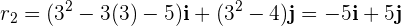
3 Calculamos el desplazamiento
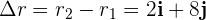
Las componentes tienen metros como unidad
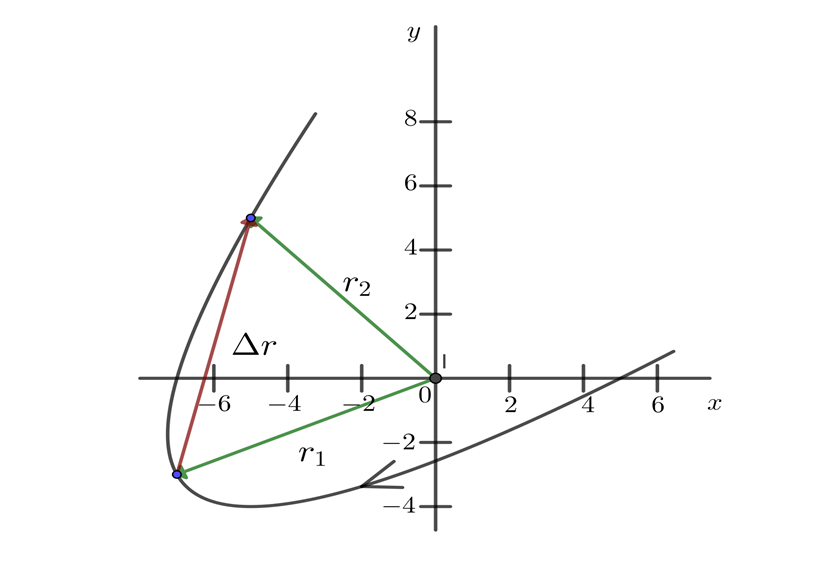
Velocidad en dos dimensiones
La velocidad promedio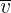 
en un intervalo de tiempo 
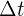es
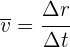
Notemos que la velocidad promedio 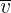es un vector, ya que el desplazamiento 
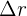es un vector y 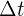es un escalar; luego la velocidad promedio tiene la misma dirección que el vector de desplazamiento
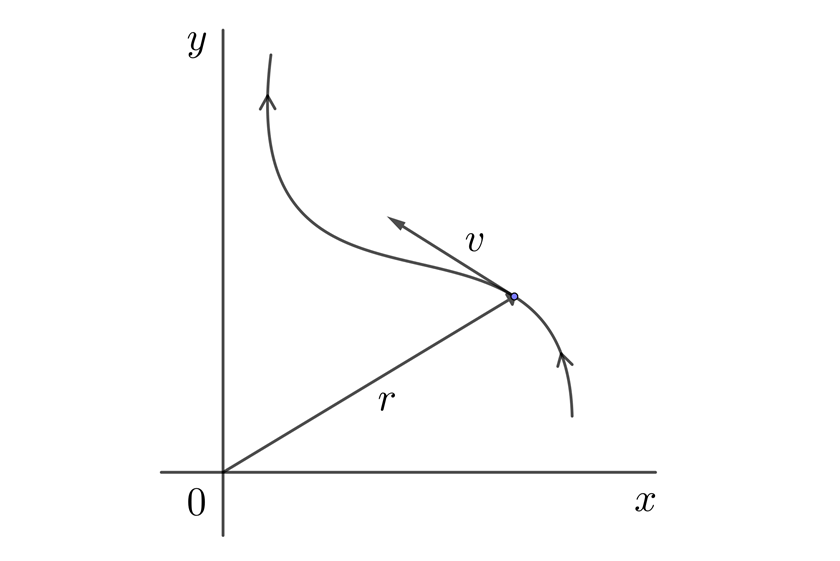
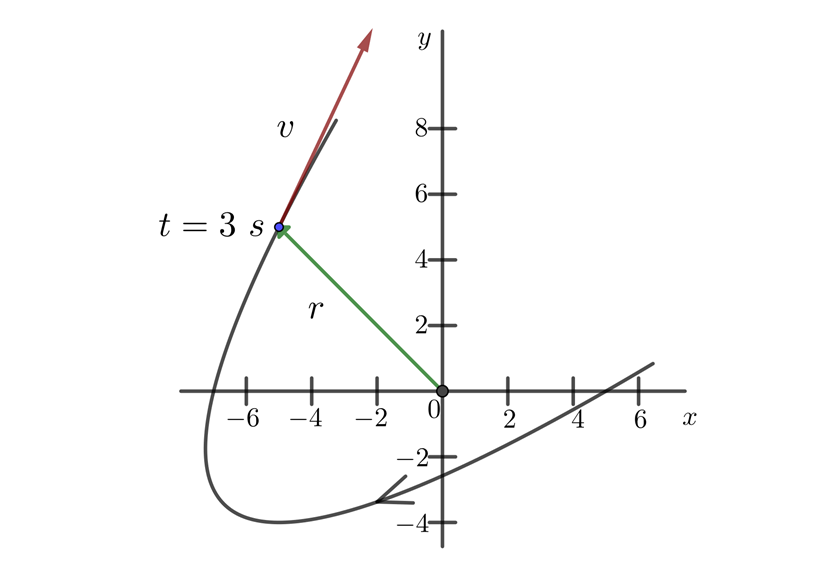
Si el intervalo de tiempo es muy pequeño, obtenemos la velocidad instantánea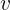 
, la cual es tangente a la trayectoria de la partícula
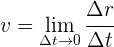
Lo anterior significa que al igual que para el caso lineal, la velocidad instantánea es igual a la derivada de la función de posición
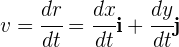
Al ser la velocidad instantánea un vector, entonces sus componentes son iguales a la derivada de las componentes de la posición
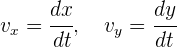
Ejemplo: Una partícula se mueve en el plano de acuerdo a 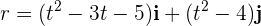. Si las coordenadas 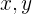están en metros y el tiempo en segundos, encuentra la velocidad promedio al moverse de 1 a 3 segundos y la velocidad cuando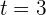
1 Calculamos el desplazamiento
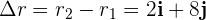
2 Calculamos la velocidad promedio para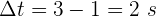 
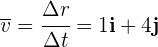
Las componentes tienen como unidades metros sobre segundos.
3 Para calcular la velocidad instantánea en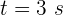 
, primero calculamos las componentes de la velocidad
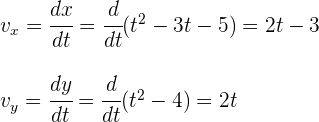
Sustituimos 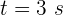y obtenemos
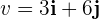
Las componentes tienen como unidades metros sobre segundos.
Aceleración en dos dimensiones
La aceleración promedio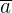 
en un intervalo de tiempo 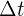es
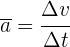
Si el intervalo de tiempo es muy pequeño, obtenemos la aceleración instantánea 
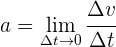
Lo anterior significa que al igual que para el caso lineal, la aceleración instantánea es igual a la derivada de la función de velocidad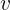
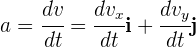
Al ser la aceleración instantánea un vector, entonces sus componentes son iguales a la derivada de las componentes de la velocidad
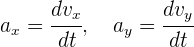
Ejemplo: Una partícula se mueve en el plano de acuerdo a 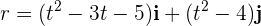. Si las coordenadas 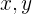están en metros y el tiempo en segundos, encuentra la aceleración cuando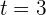
1 Para calcular la aceleración, primero requerimos la velocidad. Calculamos las componentes de la velocidad
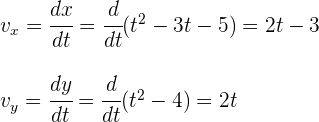
2 Calculamos las componentes de la aceleración
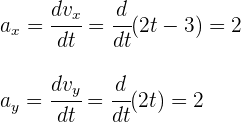
Sustituimos 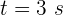y obtenemos
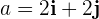
Las componentes tienen como unidades metros sobre segundos cuadrados.
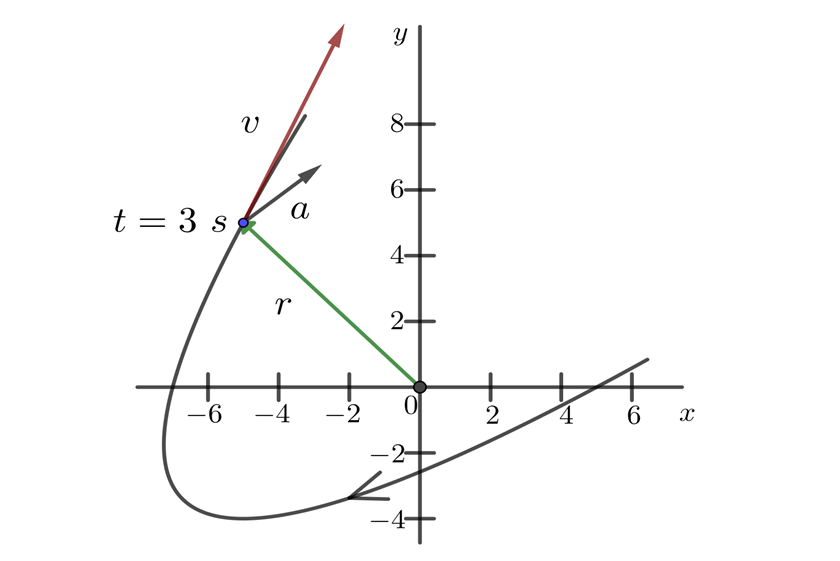
Movimiento en tres dimensiones
El movimiento en tres dimensiones es similar al de dos dimensiones, basta considerar una tercera componente 
y aplicar los mismos procesos que para dos dimensiones
Posición y desplazamiento
Si a tiempo 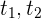la partícula se encuentra en la posición 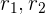respectivamente, el desplazamiento o cambio de posición en el intervalo de tiempo 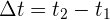, es el vector
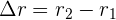
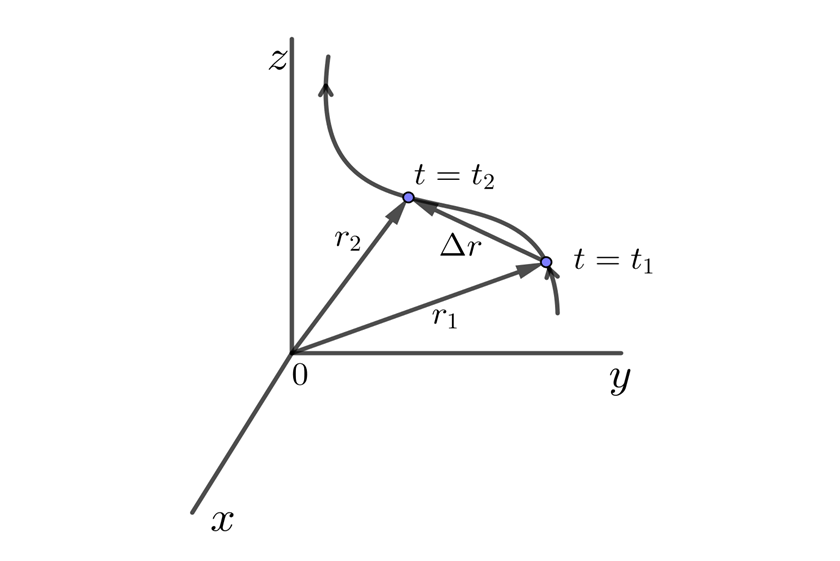
Velocidad en tres dimensiones
La velocidad promedio 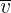en un intervalo de tiempo 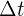es
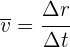
Si el intervalo de tiempo es muy pequeño, obtenemos la velocidad instantánea 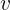, la cual es tangente a la trayectoria de la partícula
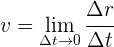
Lo anterior significa que al igual que para el caso lineal, la velocidad instantánea es igual a la derivada de la función de posición
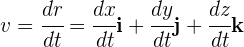
Las componentes de la velocidad son la derivada de las componentes de la posición
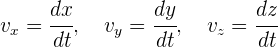
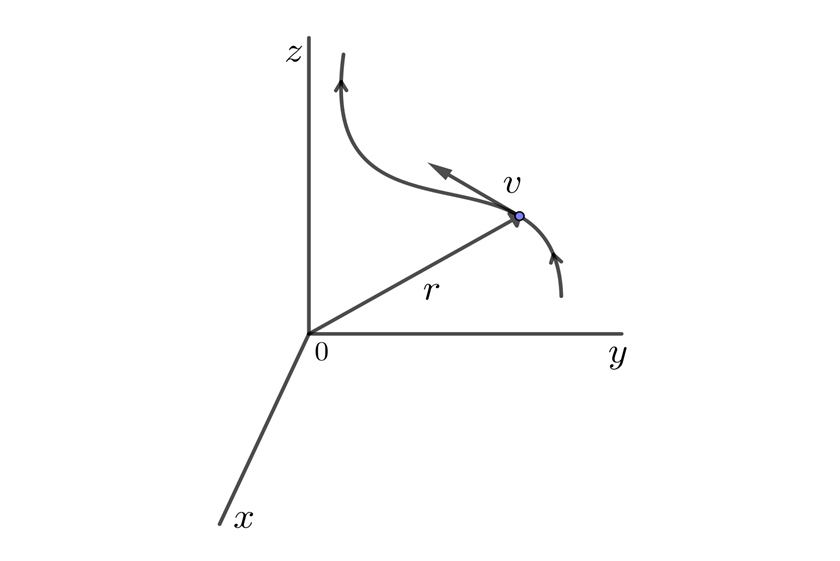
Aceleración en tres dimensiones
La aceleración promedio 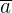en un intervalo de tiempo 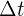es
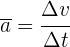
Si el intervalo de tiempo es muy pequeño, obtenemos la aceleración instantánea
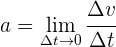
Lo anterior significa que al igual que para el caso de dimensión 2, la aceleración instantánea es igual a la derivada de la función de velocidad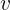
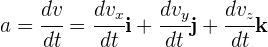
Al ser la aceleración instantánea un vector, entonces sus componentes son iguales a la derivada de las componentes de la velocidad
Ejemplo: Una partícula se mueve en el espacio de acuerdo a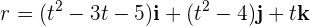 
. Si las coordenadas 
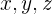están en metros y el tiempo en segundos, encuentra la aceleración cuando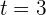
1 Para calcular la aceleración, primero requerimos la velocidad. Calculamos las componentes de la velocidad
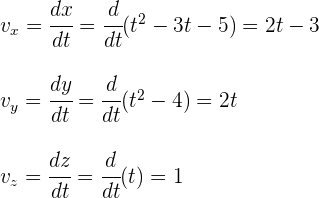
2 Calculamos las componentes de la aceleración
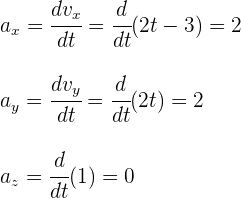
Sustituimos 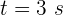y obtenemos
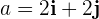
Las componentes tienen como unidades metros sobre segundos cuadrados.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker